(写题解不容易,来我的博客玩玩咯qwq~)
该题考察的知识点是边双连通分量
边双连通分量即一个无向图中,去掉一条边后仍互相连通的极大子图。(单独的一个点也可能是一个边双连通分量)
换言之,一个边双连通分量中不包含桥。
例如下图(样例)中的边双连通分量有(1),(2,3,5,6),(4),(7)
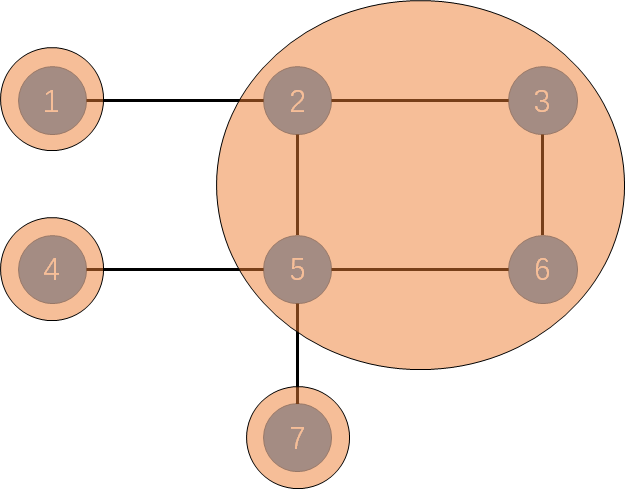
不难发现,在一个边双连通分量中,任意两点都存在至少两条互相分离的路径;(如1->2与1->3->2)
如若不在一个边双连通分量中,则可能经过桥(甚至不联通)如:2->4。
由于桥是必须通过的,所以不存在两条互相分离的路径(或没有路径)。我们要做的,就是连边将整张图变成一张边双连通图。
(正文好像才开始)
首先是找出所有边双连通分量。不难发现,边双连通分量不包含桥,因此我们只需将桥无视掉,每一个连通的子图就是一个边双连通分量。(桥的公式大家都知道吧)代码如下:
void tarjan(int u,int edge)
{
dfn[u]=low[u]=++num;
for(int i=fst[u];i!=0;i=nex[i])
{
int v=to[i];
if(!dfn[v])
{
tarjan(v,i);
low[u]=min(low[u],low[v]);
if(dfn[u]<low[v]) //桥的公式qwq
{
bridg[i]=bridg[i^1]=1;
}
}
else if(i!=(edge^1))
low[u]=min(low[u],dfn[v]);
}
}
因为在一个边双连通分量中,任意两点都存在至少两条互相分离的路径,所以我们可以将其缩为一个点。缩完点之后,我们可以把它转换成一棵树。
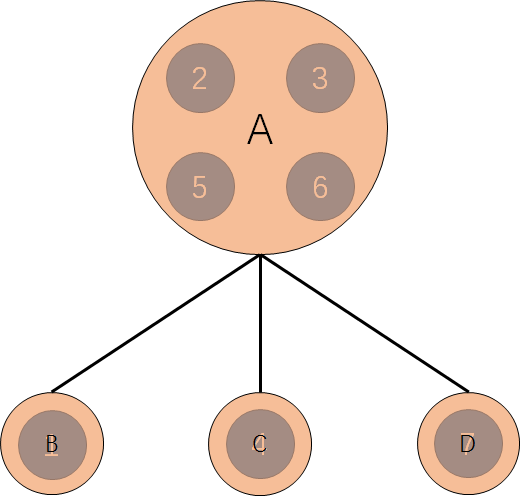
我们会发现,去掉一条边后可能会与原树不连通的,是只连有一条边的边,即叶结点(设其数量为leaf)。为令原图 边双连通(我不知道这么说对不对),我们把两个叶结点为一组用新边将其连接起来。这么看,答案似乎是leaf/2了。
且慢!!让我们看看上图。上图leaf=3,而leaf/2=1。事实上,我们需要2条边。所以最终公式为(leaf+1)/2。(终于完了qwq)
最后捋一捋思路:
-
找边双连通分量
-
缩点
-
建树,找leaf
-
ans=(leaf+1)/2
完结撒花qwqwqwqwqwq
code:
//Author:夏目贵志
#include<bits/stdc++.h>
using namespace std;
int qwwq,fst[10100],nex[10100],to[10100],a,b,cnt,num,cutn,bridg[10100],br,u[10100];
int dfn[10100],low[10100],ans,f[10100],root,pl,n,m,size,t,dcc,c[10100],du[10100];
void add(int a,int b)
{
nex[++t]=fst[a];
u[t]=a;
to[t]=b;
fst[a]=t;
return ;
}
void tarjan(int u,int edge)
{
dfn[u]=low[u]=++num;
for(int i=fst[u];i!=0;i=nex[i])
{
int v=to[i];
if(!dfn[v])
{
tarjan(v,i);
low[u]=min(low[u],low[v]);
if(dfn[u]<low[v])
{
bridg[i]=bridg[i^1]=1;
}
}
else if(i!=(edge^1))
low[u]=min(low[u],dfn[v]);
}
}
void dfs(int u)
{
c[u]=dcc;
for(int i=fst[u];i!=0;i=nex[i])
{
int v=to[i];
if(c[v]!=0||bridg[i]==1)
continue;
dfs(v);
}
}
int main()
{
scanf("%d%d",&n,&m);
t=1;
for(int i=1;i<=m;i++)
{
scanf("%d%d",&a,&b);
add(a,b);add(b,a);
}
tarjan(1,0);
for(int i=1;i<=n;i++)
{
if(!c[i])
{
dcc++;
dfs(i);
}
}
for(int i=1;i<=m;i++)
{
if(c[u[i*2]]!=c[to[i*2]])
{
du[c[u[i*2]]]++;
du[c[to[i*2]]]++;
}
}
for(int i=1;i<=dcc;i++)
{
if(du[i]==1)
br++;
}
cout<<(br+1)/2;
return 0;
}