Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)
You have the following 3 operations permitted on a word:
a) Insert a character
b) Delete a character
c) Replace a character
题意:通过每次只能插入、删除、替换一个字符,将给定字符word1转换为word2需要多少步。
思路:动态规划,维护一个二维数组,其中,dp[i][j]表示,word1.substr(0,i)转换为word2.substr(0,j)(substr的区间是前闭后开型)最少需要的步数。若是当前字符,word1[i-1]等于word2[j-1],则说明,word1从substr(0,i-2)转换为word2不需要三种操作中的任一种,即:dp[i][j]=dp[i-1][j-1];若不相等,则由有三种情:从二维数组中,左、左上、上,中三种可以到达当前值的变化方式中选取最小值,然后加1即可。此时状态转移方程是:dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j],dp[i][j-1])),规律还是相对比较难想的,多想意义。如当word1=“word”,word2=“wild”,二维数组如下:
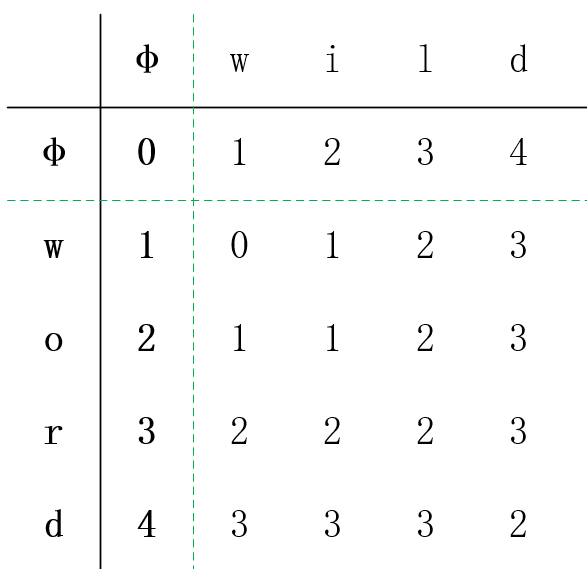
代码如下:
1 class Solution { 2 public: 3 int minDistance(string word1, string word2) 4 { 5 int len1=word1.size(),len2=word2.size(); 6 int dp[len1+1][len2+1]; 7 //初始化 8 for(int i=0;i<=len1;++i) dp[i][0]=i; 9 for(int i=0;i<=len2;++i) dp[0][i]=i; 10 11 for(int i=1;i<=len1;++i) 12 { 13 for(int j=1;j<=len2;++j) 14 { 15 if(word1[i-1]==word2[j-1]) 16 dp[i][j]=dp[i-1][j-1]; 17 else 18 dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j],dp[i][j-1]))+1; 19 } 20 } 21 return dp[len1][len2]; 22 } 23 };