重大错误说明 : 栈顶的指针始终是指向最后一个入栈元素的位置的,不是最后一个入栈元素的位置上面!请读者留意 (PS : 后来又看了一下,好像也不是什么大问题...)
上一篇 :
栈论 : 递归与栈式访问,如何用栈实现所有递归操作(基础知识篇)
2.函数调用底层篇(了解递归调用的硬件实现)
一开始,main函数没有调用add之前他的栈帧如下图,当然,下面只是简略介绍,实际上内存布局比下面更复杂(省略了寄存器等)。
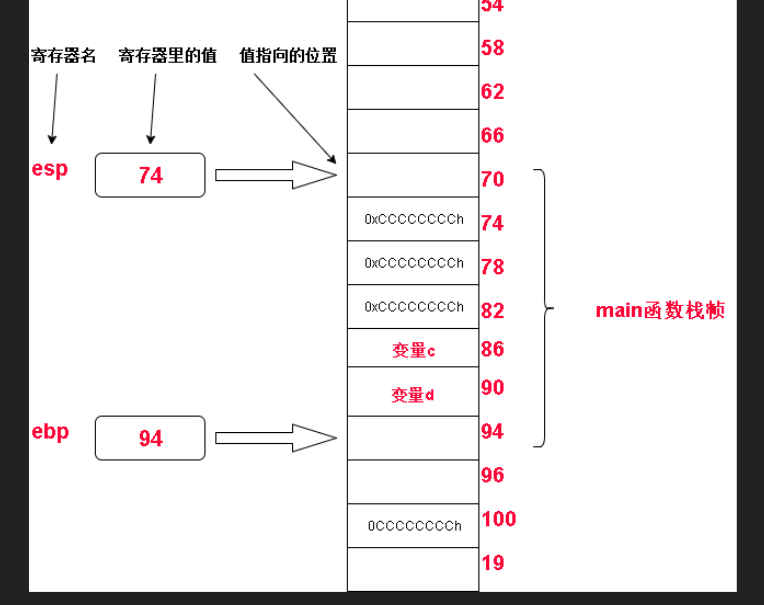
当要调用add函数的时候main 将 自己的变量拷贝后压入栈中,我们称之为“形参”
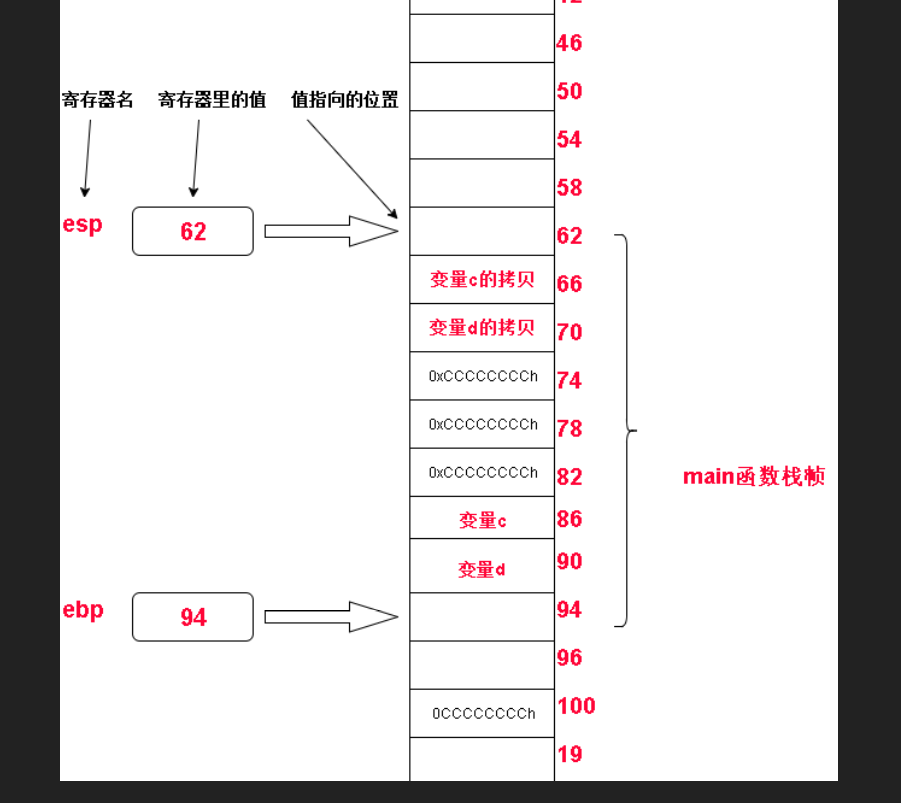
上图中变量c 和变量d的拷贝就是所谓的”形参“
接下来将main函数的ebp地址压入栈中保存,以便add函数调用完之后恢复main在内存中的栈帧

接着 就是重要的环节,add函数的栈帧创建,add函数的栈帧创建在add函数自己的操作里。
没想到吧?add函数的栈帧是add函数自己创建的。一般的思维都是父对象为子对象创建空间,再让子对象自己发挥,可能这是比较袒护孩子的行为吧,你看函数调用却是让自己的孩子去开创天地,值得学习。(当然 这是win10下汇编的得出的结果,可能不同系统不一样)
add函数本身操作 :
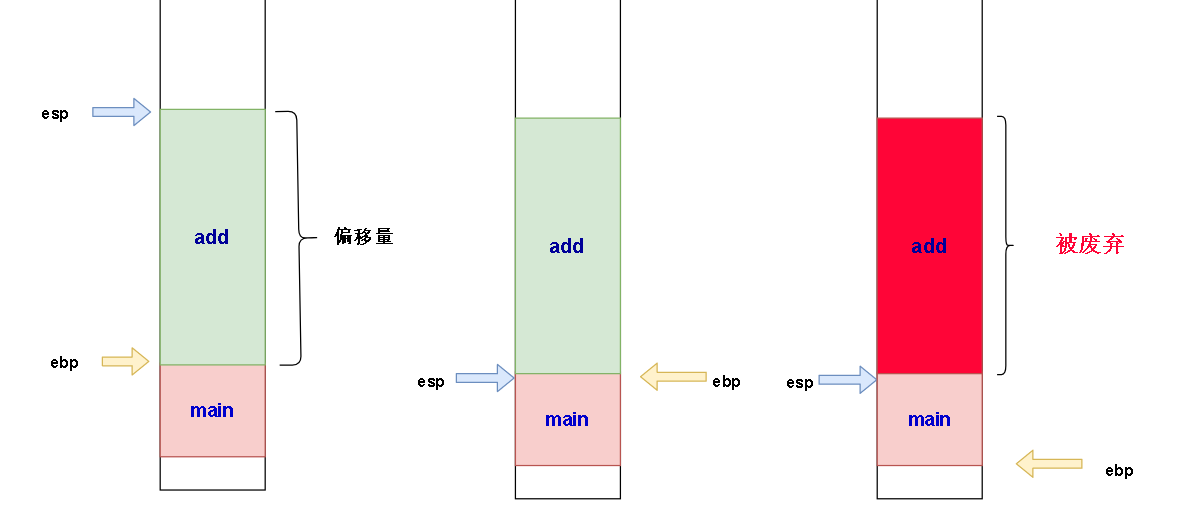
1.将esp 的值赋给ebp,这里的ebp就是add函数自己栈帧的栈底了。
2.让esp = esp - X ; X是一个位移量,表示esp要上移,esp上移的这个位移量差不多是add函数栈帧的大小。(还有一些寄存器之类的会占用空间,忽略不计)
如图:
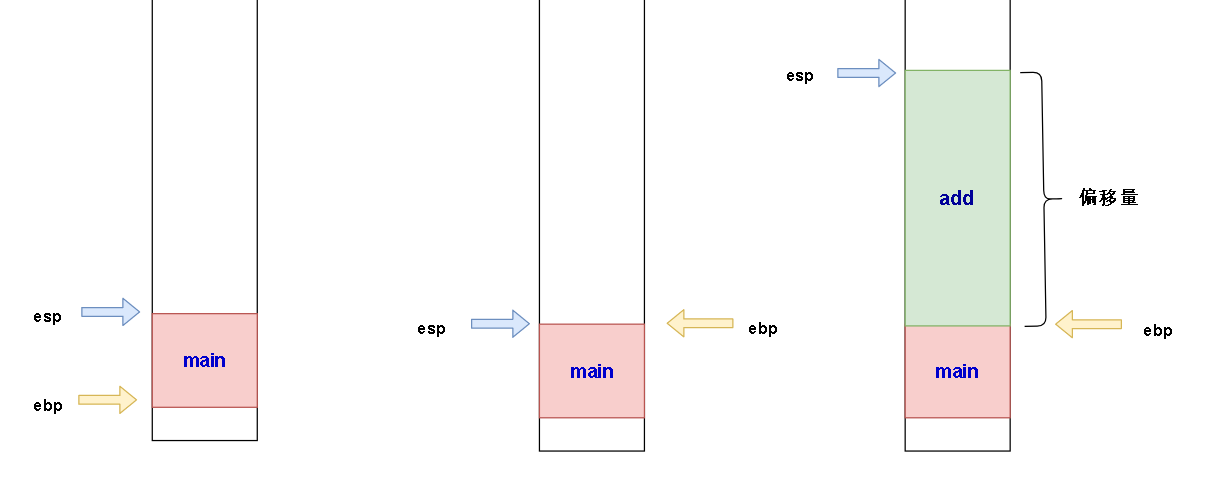
这时候的栈应该是这样的
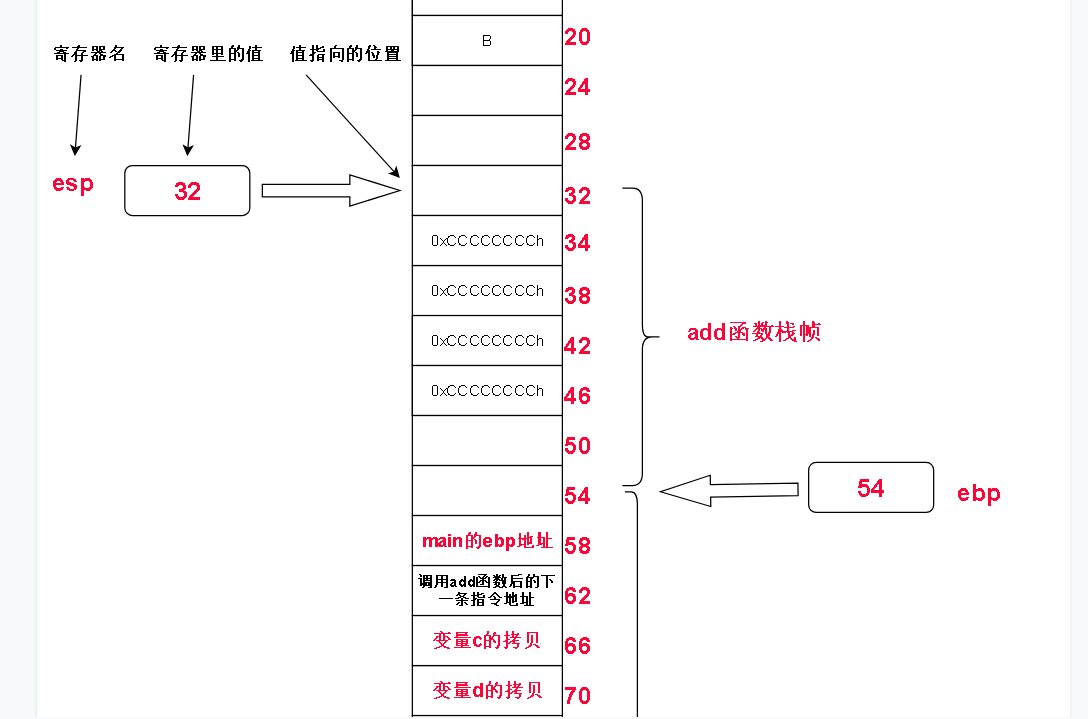
接下来,涉及到最重要环节!栈帧之间的通信
add函数的内部操作是 两个数相加,这两个数是形参,难道在add函数的栈帧中要访问在main函数栈帧中的形参吗?没错,就是直接访问。
我们来看看a + b 的汇编过程

对汇编不了解的同学可以先把 eax理解成一个变量,这个变量不在内存中(当然也就不在我们的栈区中)。mov是放进去的意思,理解把逗号右边的值放到(赋给)左边变量上(eax)去。 add是把逗号左右两边的数加起来,放到左边去。
我们发现,a + b 无非是把 ebp + 8, ebp + 12(十六进制数0Ch的十进制数)读取到的值加起来并且放到eax变量里而已。
而从 ebp + 8 和 ebp + 12 读取到的正好是main函数栈帧中的形参
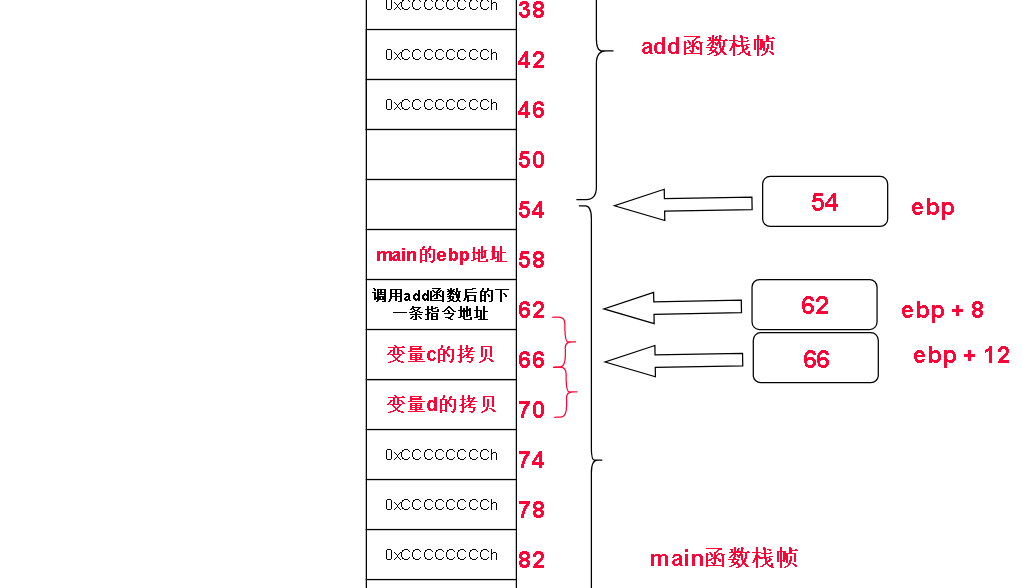
栈帧通信总结1.
子函数直接调用父函数栈帧内的形成,访问父函数
这是子向父索求信息,那么父向子索取信息呢?聪明的你可能已经猜到了,返回值!
子函数返回过程:
子函数完成之后,子函数的栈帧会被废弃掉
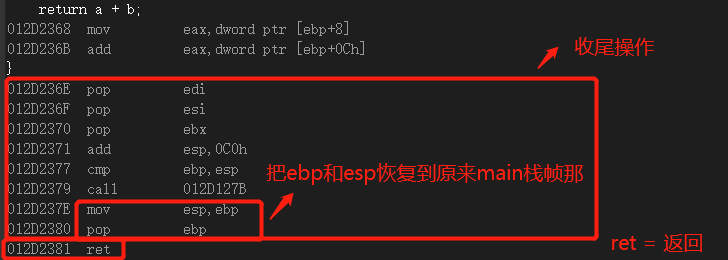
上面大圈里的小圈,两句汇编就是把栈顶和栈底移动回原来的main栈帧处。
在我们刚刚看到的a+b之后,子函数已经没什么大动作了,也就是说我们操作完之后的数是放在eax里的。
父函数就是通过访问子函数结束后遗留在eax中的数来和子函数通信,也就是说,eax里的是子函数的返回值!
从汇编也可以看到main在调用完add函数之后,为e赋值的时候直接访问了eax;

add esp,8
这句还是要好好说一说的,子函数返回之后esp还在形参的上面,既然子函数完成了,形参也没必要存在,于是需要把他们废弃掉,废弃的方法是把他们移除esp和ebp之间,也就是让esp下降就好了。
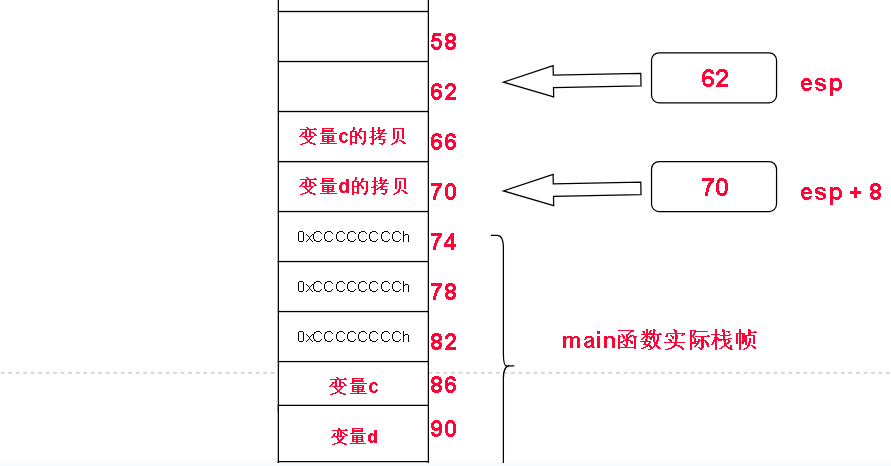
栈帧通信总结2.
父函数直接访子函数在EAX中遗留的返回值
综上,我们得出以下几点结论。
1.子函数直接调用父函数栈帧内的形成,访问父函数
2.父函数直接访子函数在EAX中遗留的返回值
3.父函数调用子函数,子函数创建栈帧,子函数完成后子函数的栈帧销毁
下一篇 :
栈论 : 递归与栈式访问,如何用栈实现所有递归操作(幼儿园题目篇)
护眼绿:
没人看的结语:
首先很感谢你看到这里,辛苦了。
文章中某些地方可能不正确或不准确,代码也可能不够高效可读,希望读者能够帮忙指正,共同学习进步。