一、算法思想
快速排序,顾名思义,效率比较于其他算法,效率比较高。《算法导论》也专门对其进行讲解。其算法设计使用分治思想,如下:
1)从数组A[p...r]中选择一个元素,将数组划分成两个子数组:A[p...q-1]和A[q+1...r],使得A[p...q-1]中的元素全部小于等于A(q),使得A[q+1...r]中的元素全部大于A(q);
2)通过递归调用快速排序,分别对A[p...q-1]和A[q+1...r]排序;
3)因为两个子数组是就地排序,因此它们的合并不需要操作,整个数组A[p...r]已经排序;
二、算法示意图
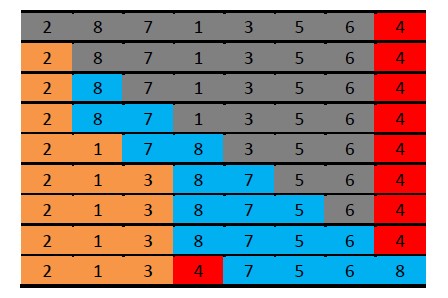
图中所示只是代表一次分的过程,其中红色的4代表选中的用于分割的数组元素,灰色部分代表待排序的过程,黄色部分代表小于等于选中元素的数组元素,蓝色部分则代表大于选中元素的数组元素。解释一下这一次过程的形成:
第一行表示待排序的数组,其中默认选择待排序数组的最后一个元素作为中间元素进行分割。第二行我们看第一个元素,2比4小,不需要操作,第三行看8,8比4大,也不需要操作,因为由图可以看出来,第三行正好是‘≤4’,‘>4’,待排序元素,选择元素这样一个序列;第四行看7,发现7>4,也不需要操作,第五行看1,1这个时候比4小,应该和2放在一起,则最快的方法是和‘>4’序列块的第一个元素交换,因此将滴4行元素的1和8交换就得到第五行;同理,第六行看的是3,将第五行的3和7交换就得到第六行。如此下去,直到倒数第二行,已经没有待排序元素了。这个时候,将交换元素和‘>4’序列块的第一个元素交换,即4和8交换,就形成最后一行,最终的形式是‘≤选中元素(4)’,选择元素,‘>选中元素(4)’这样一个序列。然后再对‘≤选中元素(4)’和‘>选中元素(4)’两个序列块,即最后一行的黄色部分和蓝色部分分别执行相同过程,最终完成排序。
从描述中可以看到:
1)选择最后一个元素作为选择元素,可以最大程度降低元素交换的复杂性;
2)如果遍历找到比选中元素小或者相等的元素,则需要和‘>选中元素’序列块的第一个元素交换,这样就可以和‘≤选中元素’的序列块最快的接合到一起;
3)如果遍历找到比选中元素大的元素,则不需要操作;
4)为了快速的交换,我们需要对序列添加多个指针:指向‘≤选中元素’的序列块的第一个和最后一个,指向选中元素;
三、Java代码
先来看看一种简单直接的实现:
1 //@wiki 2 public class Quicksort { 3 public static final Random RND = new Random(); 4 5 private static void swap(Object[] array, int i, int j) { 6 Object tmp = array[i]; 7 array[i] = array[j]; 8 array[j] = tmp; 9 } 10 11 private static <E> int partition(E[] array, int begin, int end, Comparator<? super E> cmp) { 12 int index = begin + RND.nextInt(end - begin + 1); 13 E pivot = array[index]; 14 swap(array, index, end); 15 for (int i = index = begin; i < end; ++ i) { 16 if (cmp.compare(array[i], pivot) <= 0) { 17 swap(array, index++, i); 18 } 19 } 20 swap(array, index, end); 21 return (index); 22 } 23 24 private static <E> void qsort(E[] array, int begin, int end, Comparator<? super E> cmp) { 25 if (end > begin) { 26 int index = partition(array, begin, end, cmp); 27 qsort(array, begin, index - 1, cmp); 28 qsort(array, index + 1, end, cmp); 29 } 30 } 31 32 public static <E> void sort(E[] array, Comparator<? super E> cmp) { 33 qsort(array, 0, array.length - 1, cmp); 34 } 35 36 }
这段代码应该比较好懂,因为和上面的解说基本一样,qsort函数是一个递归函数,其中用到一个partition函数进行分割。这段代码有以下几个需要注意的地方:
1)使用了泛型和Comparator,这样更具扩展性;
2)注意12~14行,前面解说中我们默认选择的是待排序序列的最后一个元素,但是这里不是,这里是随机产生一个选择元素,然后为了交换元素的方便,首先将这个选择元素交换到序列的最后面去,划归到解说中的形式;
四、算法复杂度
最坏情况划分:在划分过程中产生两个区域,分别包含n-1个元素和1和0元素的时候(这个时候选中的元素是序列中最大或者最小的元素)。假设算法的每一次递归调用的时候都出现了这种不对称的划分,划分的时间代价为θ(n)。因为对一个大小为0的数组进行递归调用以后,返回T(0)=θ(1),所以算法的运行时间可以递归的表示为:
T(n) = T(n-1) + θ(n) + θ(1)
利用替换法,可以比较直接的证明其解为T(n)=θ(n^2)。
最好情况划分:即划分的时候,序列正好划分为两半,有时候序列元素个数为奇数,不能相等,则左右可以相差1,这个时候,其表达式为:
T(n) ≤ 2T(n/2) + θ(n)
可以解得递归式的解为T(n)=O(nlogn)。