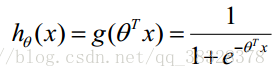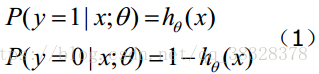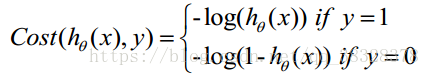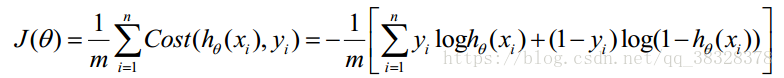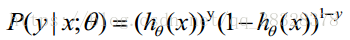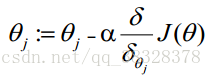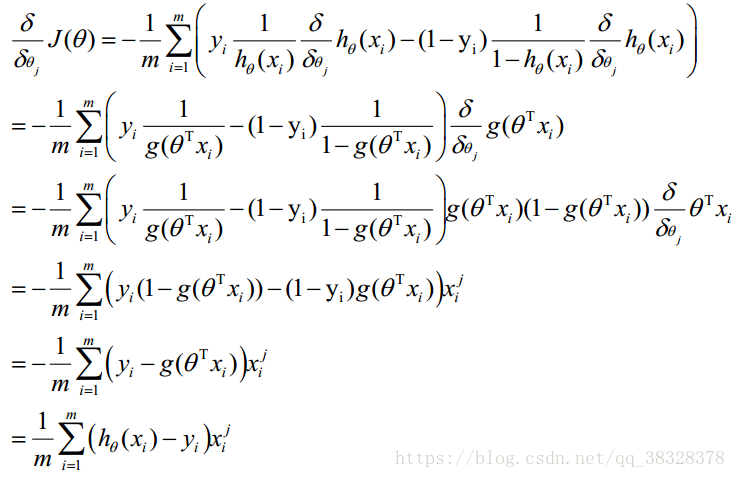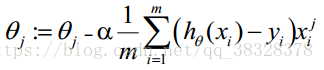逻辑回归--简介
逻辑回归(Logistic Regression)就是这样的一个过程:面对一个回归或者分类问题,建立代价函数,然后通过优化方法迭代求解出最优的模型参数,然后测试验证我们这个求解的模型的好坏。
Logistic回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别)。
回归模型中,y是一个定性变量,比如y=0或1,logistic方法主要应用于研究某些事件发生的概率。
逻辑回归--优缺点
优点:
1、速度快,适合二分类问题 ;
2、简单易于理解,直接看到各个特征的权重 ;
3、能容易地更新模型吸收新的数据 ;
缺点:
1、对数据的场景的适应能力有局限性,不如决策树算法适应性强;
逻辑回归--用途
用途:
1、寻找危险因素:寻找某一疾病的危险因素等;
2、预测:根据模型,预测在不同的自变量情况下,发生某病或某种情况的概率有多大;
3、判别:实际上跟预测有些类似,也是根据模型,判断某人属于某病或属于某种情况的概率有多大,也就是看一下这个人有多大的可能性是属于某病
逻辑回归--原理
Logistic Regression和Linear Regression的原理是相似的,按照我自己的理解,可以简单的描述为这样的过程:
(1)找一个合适的预测函数(Andrew Ng的公开课中称为hypothesis),一般表示为h函数,该函数就是我们需要找的分类函数,它用来预测输入数据的判断结果。这个过程时非常关键的,需要对数据有一定的了解或分析,知道或者猜测预测函数的“大概”形式,比如是线性函数还是非线性函数。
(2)构造一个Cost函数(损失函数),该函数表示预测的输出(h)与训练数据类别(y)之间的偏差,可以是二者之间的差(h-y)或者是其他的形式。综合考虑所有训练数据的“损失”,将Cost求和或者求平均,记为J(θ)函数,表示所有训练数据预测值与实际类别的偏差。
(3)显然,J(θ)函数的值越小表示预测函数越准确(即h函数越准确),所以这一步需要做的是找到J(θ)函数的最小值。找函数的最小值有不同的方法,Logistic Regression实现时有的是梯度下降法(Gradient Descent)。
逻辑回归--具体过程
一、构造预测函数
Logistic回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别),所以利用了Logistic函数(或称为Sigmoid函数),函数形式为:
Sigmoid 函数在有个很漂亮的“S”形,如下图所示:
下面左图是一个线性的决策边界,右图是非线性的决策边界:
对于线性边界的情况,边界形式如下:
构造预测函数为:
函数
二、构造损失函数
Cost 函数和 J 函数如下,它们是基于最大似然估计推导得到的:
下面详细说明推导的过程:
(1)式综合起来可以写成:
取似然函数为:
对数似然函数为:
最大似然估计就是求使 取最大值时的θ,其实这里可以使用梯度上升法求解,求得的θ就是要求的最佳参数。但是,在Andrew Ng的课程中将 J(θ) 取为下式,即:
取最大值时的θ,其实这里可以使用梯度上升法求解,求得的θ就是要求的最佳参数。但是,在Andrew Ng的课程中将 J(θ) 取为下式,即:
因为乘了一个负的系数-1/m,所以取 J(θ) 最小值时的θ为要求的最佳参数。
三、梯度下降法求的最小值
求J(θ)的最小值可以使用梯度下降法,根据梯度下降法可得θ的更新过程:
式中为α学习步长,下面来求偏导:
θ更新过程可以写成:
逻辑回归--实例
# -*- coding: utf-8 -*-
from numpy import *
import matplotlib.pyplot as plt
#从文件中加载数据:特征X,标签label
def loadDataSet():
dataMatrix=[]
dataLabel=[]
#这里给出了python 中读取文件的简便方式
f=open('testSet.txt')
for line in f.readlines():
#print(line)
lineList=line.strip().split()
dataMatrix.append([1,float(lineList[0]),float(lineList[1])])
dataLabel.append(int(lineList[2]))
#for i in range(len(dataMatrix)):
# print(dataMatrix[i])
#print(dataLabel)
#print(mat(dataLabel).transpose())
matLabel=mat(dataLabel).transpose()
return dataMatrix,matLabel
#logistic回归使用了sigmoid函数
def sigmoid(inX):
return 1/(1+exp(-inX))
#函数中涉及如何将list转化成矩阵的操作:mat()
#同时还含有矩阵的转置操作:transpose()
#还有list和array的shape函数
#在处理矩阵乘法时,要注意的便是维数是否对应
#graAscent函数实现了梯度上升法,隐含了复杂的数学推理
#梯度上升算法,每次参数迭代时都需要遍历整个数据集
def graAscent(dataMatrix,matLabel):
m,n=shape(dataMatrix)
matMatrix=mat(dataMatrix)
w=ones((n,1))
alpha=0.001
num=500
for i in range(num):
error=sigmoid(matMatrix*w)-matLabel
w=w-alpha*matMatrix.transpose()*error
return w
#随机梯度上升算法的实现,对于数据量较多的情况下计算量小,但分类效果差
#每次参数迭代时通过一个数据进行运算
def stocGraAscent(dataMatrix,matLabel):
m,n=shape(dataMatrix)
matMatrix=mat(dataMatrix)
w=ones((n,1))
alpha=0.001
num=20 #这里的这个迭代次数对于分类效果影响很大,很小时分类效果很差
for i in range(num):
for j in range(m):
error=sigmoid(matMatrix[j]*w)-matLabel[j]
w=w-alpha*matMatrix[j].transpose()*error
return w
#改进后的随机梯度上升算法
#从两个方面对随机梯度上升算法进行了改进,正确率确实提高了很多
#改进一:对于学习率alpha采用非线性下降的方式使得每次都不一样
#改进二:每次使用一个数据,但是每次随机的选取数据,选过的不在进行选择
def stocGraAscent1(dataMatrix,matLabel):
m,n=shape(dataMatrix)
matMatrix=mat(dataMatrix)
w=ones((n,1))
num=200 #这里的这个迭代次数对于分类效果影响很大,很小时分类效果很差
setIndex=set([])
for i in range(num):
for j in range(m):
alpha=4/(1+i+j)+0.01
dataIndex=random.randint(0,100)
while dataIndex in setIndex:
setIndex.add(dataIndex)
dataIndex=random.randint(0,100)
error=sigmoid(matMatrix[dataIndex]*w)-matLabel[dataIndex]
w=w-alpha*matMatrix[dataIndex].transpose()*error
return w
#绘制图像
def draw(weight):
x0List=[];y0List=[];
x1List=[];y1List=[];
f=open('testSet.txt','r')
for line in f.readlines():
lineList=line.strip().split()
if lineList[2]=='0':
x0List.append(float(lineList[0]))
y0List.append(float(lineList[1]))
else:
x1List.append(float(lineList[0]))
y1List.append(float(lineList[1]))
fig=plt.figure()
ax=fig.add_subplot(111)
ax.scatter(x0List,y0List,s=10,c='red')
ax.scatter(x1List,y1List,s=10,c='green')
xList=[];yList=[]
x=arange(-3,3,0.1)
for i in arange(len(x)):
xList.append(x[i])
y=(-weight[0]-weight[1]*x)/weight[2]
for j in arange(y.shape[1]):
yList.append(y[0,j])
ax.plot(xList,yList)
plt.xlabel('x1');plt.ylabel('x2')
plt.show()
if __name__ == '__main__':
dataMatrix,matLabel=loadDataSet()
#weight=graAscent(dataMatrix,matLabel)
weight=stocGraAscent1(dataMatrix,matLabel)
print(weight)
draw(weight)