郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

ABSTRACT
SAC是用于连续动作设置的最先进的RL算法,不适用于离散动作设置。但是,许多重要的设置都涉及离散动作,因此,在这里我们导出了适用于离散动作设置的SAC算法的替代版本。然后,我们证明了,即使没有任何超参数调整,它在Atari套件中精选的游戏中也可以与调整后的无模型最新技术相媲美。
1 Introduction
RL近年来取得了著名的进步,已成功应用于棋盘游戏[Silver et al., 2017],视频游戏[Mnih et al., 2015]和机器人任务[OpenAI et al., 2018]。但是,RL在现实世界中的广泛应用仍然很缓慢,这主要是因为样本效率差被Wu et al. (2017)视为"RL中的主要关注点"。
Haarnoja et al. (2018)提供了SAC算法,该算法有助于在连续动作设置中解决此问题。它在多个具有挑战性的连续控制域中实现了无模型的最新样本效率。但是,许多域涉及离散而不是连续的动作,因此在这些环境中,SAC当前不适用。本文推导了适用于离散动作域的SAC版本,然后证明了从Atari [Bellemare et al., 2013]套件选择游戏的样本效率方面,它与离散动作域的无模型最新技术相比具有竞争力。
我们进行如下操作:首先,我们解释Haarnoja et al. (2018)以及Haarnoja et al. (2019)发现的连续动作设置中的SAC,然后我们导出并解释创建算法的离散动作版本所需的更改,最后我们在Atari套件上测试离散动作算法。
2 Soft Actor-Critic
SAC [Haarnoja et al., 2018]试图找到一种最大化最大熵目标的策略:
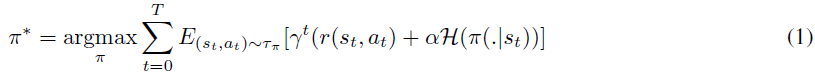

为了最大化目标,作者使用软策略迭代,这是在最大熵框架内交替进行策略评估和策略改进的方法。
策略评估步骤涉及计算策略π的价值。为此,他们首先将软状态价值函数定义为:
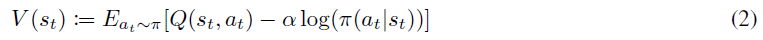
然后他们证明,在表格形式的设置中(即状态空间是离散的),我们可以从随机初始化的函数Q: S x A → R开始获得软Q函数,并重复应用以下给出的修改后的Bellman备份运算符Tπ:
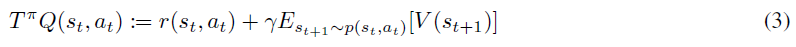
其中p: S x A → S给定当前状态和动作,给出下一状态的分布。
他们解释说,在连续状态(而不是表格形式)中,我们首先使用带有参数θ的神经网络来对软Q函数Qθ(st, at)进行参数化。然后我们训练软Q函数以最小化软Bellman残差:
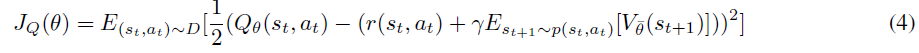
其中D是过去经验的回放缓存,而![]() 是使用Q的目标网络和从回放缓存中采样经验后使用(2)的蒙特卡洛估计来估计的。
是使用Q的目标网络和从回放缓存中采样经验后使用(2)的蒙特卡洛估计来估计的。
然后,策略改进步骤包括朝着将其可获得的奖励最大化的方向更新策略。为此,他们使用在策略评估步骤中计算出的软Q函数来指导对策略的更改。具体来说,他们将策略更新为新的软Q函数的指数形式。但是,由于他们也希望策略易于处理,因此将可能的策略限制在参数化的分布族中(例如高斯分布)。为了解决这个问题,在将策略更新为软Q函数的指数之后,他们随后使用根据Kullback-Leibler散度定义的信息投影将其投影回可接受策略的空间。因此,总体而言,策略改进步骤如下:
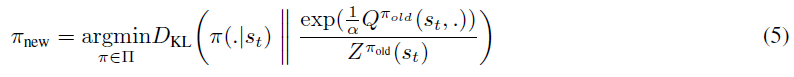
他们注意到,划分函数![]() 是很难处理的,但是对于新策略而言,它不会造成梯度,因此可以忽略。
是很难处理的,但是对于新策略而言,它不会造成梯度,因此可以忽略。
在连续状态设置中,他们使用带有输出均值和协方差的参数Φ的神经网络对策略πΦ(at|st)进行参数化,然后将其用于定义高斯策略。然后,通过将期望的KL散度(5)乘以温度参数α并忽略划分函数![]() 来对其进行最小化(因为它不会影响梯度),从而学习策略参数:
来对其进行最小化(因为它不会影响梯度),从而学习策略参数:
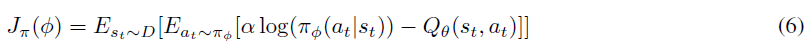
这涉及对策略的输出分布求期望,这意味着误差不能以正常方式反向传播。为了解决这个问题,他们使用重参数化技巧[Kingma and Welling, 2013]——而不是直接使用策略网络的输出来形成随机动作分布,而是将其输出与从球形高斯采样的输入噪声向量相结合。例如,在一维情况下,我们的网络输出均值m和标准差s。我们可以直接对动作进行随机采样a ~ N(m, s),但随后无法通过该操作反向传播误差。因此,我们改为执行a = m + sε,其中ε ~ N(0, 1)允许我们像往常一样反向传播。为了表示他们正在以这种方式重参数化策略,他们写道:

其中εt ~ N(0, I)。新的策略目标将变为:
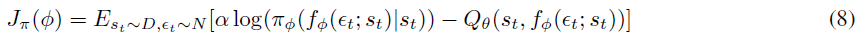
其中根据fΦ隐式定义了πΦ。然后他们继续证明,在表格式环境中,如上所述的策略评估与策略改进之间的交替将收敛于最优策略。
Haarnoja et al. (2019)还提供了一种学习温度参数的可选方法,因此我们无需将其设置为超参数。它们提供了温度目标值的长期推导,但是,由于细节与我们推导离散动作版本的SAC并不严格相关,因此在此不再赘述。然而,他们获得的温度参数的最终目标是相关的,并由以下公式给出:
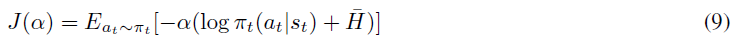
其中![]() 是一个常数向量(等于表示目标熵的超参数)。由于期望算子的存在,他们不能直接最小化这个公式,因此他们在从回放缓存采样经验后,将其最小化。
是一个常数向量(等于表示目标熵的超参数)。由于期望算子的存在,他们不能直接最小化这个公式,因此他们在从回放缓存采样经验后,将其最小化。
最后,在实际应用中,作者维护了两个单独训练的软Q网络,并以其两个输出的最小值作为软Q网络的输出。他们这样做是因为Fujimoto, Hoof, and Meger (2018)表明,这有助于遏制状态-价值的高估。
3 Soft Actor-Critic for Discrete Action Settings (SAC-Discrete)
现在,我们得出上述SAC算法的离散动作版本。首先要注意的是,实现以上目标所涉及的所有关键步骤都可以是连续/离散动作。所发生的所有变化是现在![]() 输出概率(而不是密度)。因此,三个目标函数JQ(θ) (4),Jπ(Φ) (6)和J(α) (9)仍然成立。但是,我们必须对优化这些目标函数的过程进行五项重要更改:
输出概率(而不是密度)。因此,三个目标函数JQ(θ) (4),Jπ(Φ) (6)和J(α) (9)仍然成立。但是,我们必须对优化这些目标函数的过程进行五项重要更改:
- 现在,使软Q函数输出每个可能动作的Q值而不是简单地作为输入提供的动作更为有效,即我们的Q函数从Q: S x A → R到Q: S → R|A|。在我们可以采取无限多种可能的动作之前,这是不可能的。
- 现在我们的策略不再需要输出动作分布的均值和协方差,而是可以直接输出我们的动作分布。因此该策略从π: S → R2|A|改变到π: S → [0, 1]|A|,其中我们在策略的最后一层应用softmax函数,以确保其输出有效的概率分布。
- 之前,为了使软Q函数成本JQ(θ) (4)最小,我们必须从回放缓存插入采样动作,以形成软状态-价值函数的蒙特卡洛估计(2)。这是因为估计(2)中的软状态-价值函数需要对动作分布求期望。但是,现在,由于我们的动作集是离散的,因此我们可以完全恢复动作分布,因此无需形成蒙特卡洛估计,而是可以直接计算期望值。这种变化应减少我们对目标JQ(θ) (4)的估计中涉及的方差。这意味着我们将软状态-价值计算公式从(2)更改为:
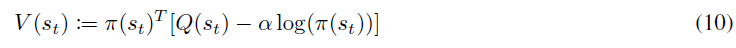
- 同样,我们可以对温度损失的计算进行相同的更改,以减少该估计的方差。温度目标从(9)变为:

- 以前,为使Jπ(Φ) (6)最小,我们必须使用重参数化技巧使梯度通过期望算子。但是,现在我们的策略输出准确的动作分布,我们可以直接计算期望值。因此,无需重参数化技巧,策略的新目标从(8)变为:
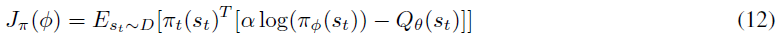
结合所有这些更改,算法1给出了具有离散动作的SAC算法(SAC-Discrete)。

4 Results
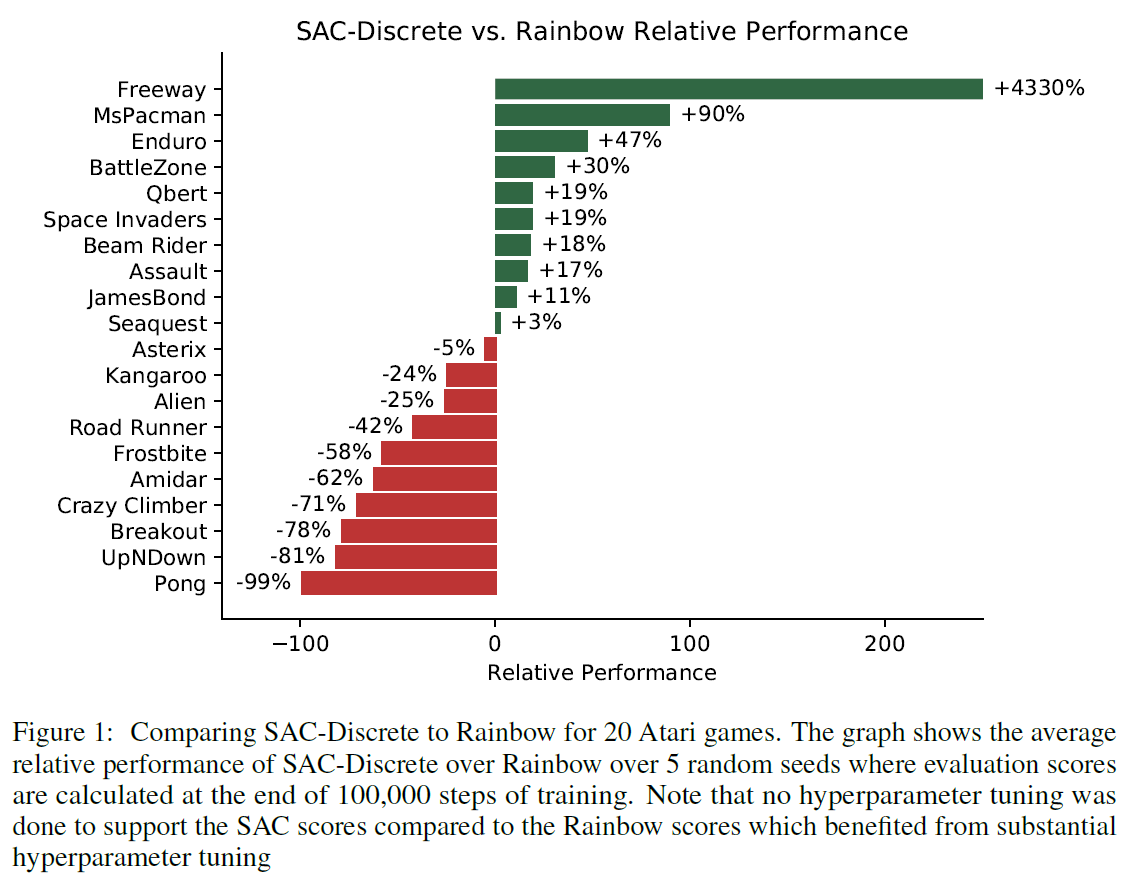
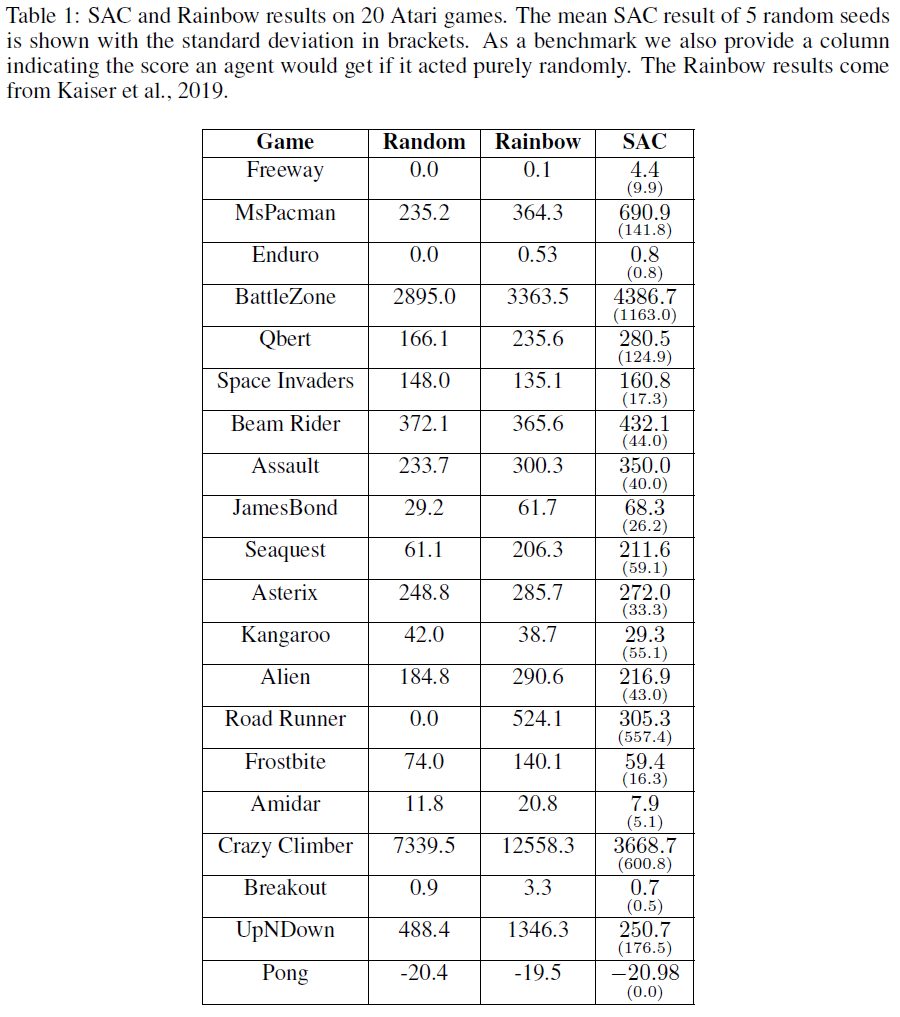
为了测试SAC-Discrete的有效性,我们在20个Atari游戏中对5个随机种子中的每一个运行100000步,并将其结果与Rainbow进行了比较,Rainbow在样本效率方面是一种最新的无模型算法。这些游戏差异很大,因此被选为先验,因此我们认为这20款游戏的结果可以很好地估计整个Atari套件中49个游戏的相对性能。我们选择将算法运行100000步,因为我们对样本效率最感兴趣,并且Kaiser et al. (2019)证明Rainbow可以在100000步之内在Atari游戏上取得重大进展。
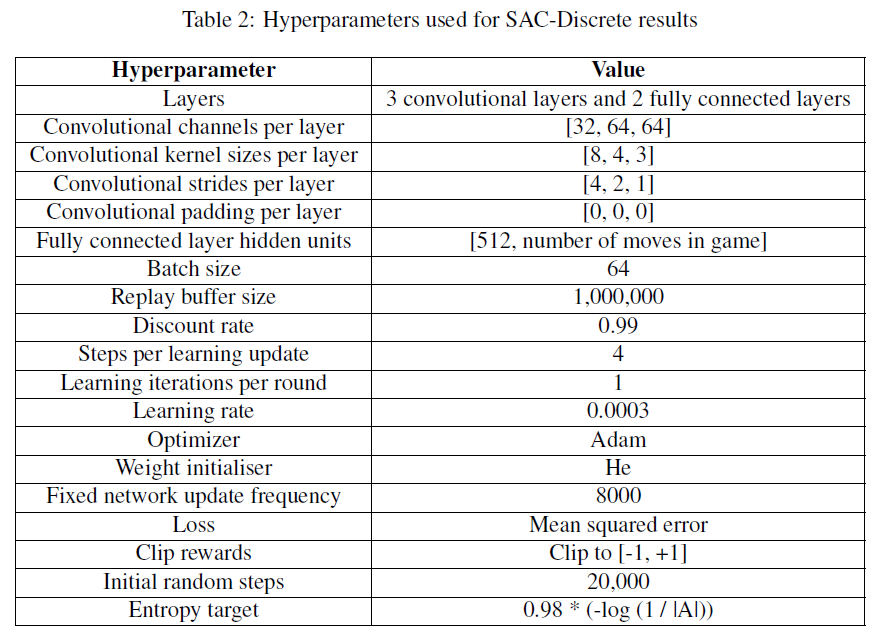
对于SAC离散动作,我们没有进行超参数调整,而是使用了Haarnoja et al. (2019)和Kaiser et al. (2019)的混合超参数。超参数可在附录B中找到。我们比较的Rainbow结果来自Kaiser et al. (2019),并且其解释是大量超参数调整的结果。1因此,我们正在将调整后的Rainbow算法与未调整的SAC算法进行比较,因此,如果我们花一些时间调整超参数,很有可能可以改进SAC的相对性能。
我们发现SAC-Discrete在20个游戏中有10个得分高于Rainbow,平均表现为-1%,最高表现为+ 4330%,最低为-99%——图1总结了结果,附录A在表中提供了这些结果。总体而言,因此,在采样效率方面,我们认为SAC-Discrete算法与Atari套件中无模型的最新技术具有相当的竞争力。
1 对于两款游戏(Enduro和SpaceInvaders),Kaiser et al. (2019)没有为Rainbow提供任何结果,因此对于这两个游戏,我们只能自行运行Rainbow算法。我们使用Dopamine[Castro et al., 2018]代码库(与Kaiser et al. (2019)一样)以及与Kaiser et al. (2019)使用相同的(调整后的)超参数进行此操作。我们在合作笔记中共享用于执行此操作的代码:https://colab.research.google.com/drive/11prfRfM5qrMsfUXV6cGY868HtwDphxaF
5 Conclusion
原始的Soft Actor-Critic算法在许多连续动作设置上都获得了最新的结果,但不适用于离散动作设置。 为了更正此问题,我们推导了一种适用于离散动作设置的算法SACDiscrete版本,并显示出即使没有任何超参数调整,它也可以与Atari套件上的无模型最新技术相媲美。 我们在项目的GitHub存储库中提供了该算法的Python实现。2
2 https://github.com/p-christ/Deep-Reinforcement-Learning-Algorithms-with-PyTorch
Appendix
A SAC and Rainbow Atari Results
B SAC-Discrete Hyperparameters