How to Combine Tree-Search Methods in Reinforcement Learning

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

AAAI 2019 Best Paper

Abstract

　　RL中大量使用了有限视野的前瞻策略，并显示出令人印象深刻的经验性成功。通常，前瞻策略是通过特定的规划方法(例如，蒙特卡洛树搜索)(例如，在AlphaZero中(Silver et al., 2017b))实现的。将规划问题称为树搜索，在这些实现中的合理实践是仅在叶子处备份价值，而在根部获得的信息除了用于更新策略外，不利用任何信息。在此，我们质疑这种方法的效力。即，后一种过程通常是不收敛的，并且不能保证其收敛性。我们提出的增强非常简单直接：使用最优树路径的回报来备份根后代的价值。这导致了γ^h-收敛过程，其中γ是折扣因子，h是树的深度。为了建立我们的结果，我们首先引入一个称为多步贪婪一致性的概念。然后，在存在注入到树搜索阶段和价值估计阶段的噪声的情况下，为上述增强的两个算法实例提供收敛速率。

1 Introduction

　　RL文献中有很大一部分与策略迭代(PI)方法有关。该算法系列包含大量经过全面分析的变体(Puterman 1994; Bertsekas and Tsitsiklis 1995)，并构成了复杂的最新技术实现的基础(Mnih et al. 2016; Silver et al. 2017b)。PI的主要机制是在策略评估和策略改进之间交替。在策略评估阶段，存在各种经过深入研究的方法。这些可能依赖于单步自举，多步蒙特卡洛回报或前两者的参数控制插值。对于策略改进阶段，理论分析主要保留给单步贪婪策略，而最近针对多步贪婪策略的主要实现表现出有希望的经验性行为(Silver et al. 2017b; Silver et al. 2017a)。

　　依靠多步前瞻策略分析的最新进展(Efroni et al. 2018a; Efroni et al. 2018b)，我们研究了一个PI方案的收敛性，该方案的改进阶段是关于价值函数的h步贪婪(对于h > 1)。可以通过动态规划(DP)或其他规划方法来计算此类策略，例如树搜索。结合采样，后者对应于(Silver et al. 2017b; Silver et al. 2017a)中采用的著名的蒙特卡洛树搜索(MCTS)算法。在这项工作中，我们表明，即使执行了部分(不准确)的策略评估并向其添加噪声，伴随着带噪的策略改进阶段，上述PI方案也以收敛因子γ^h来收敛。在这样做的同时，我们还分离出一个充分的收敛条件，我们称其为h-贪婪一致性，并将其与先前的单步贪婪相关文献联系起来。

　　上述PI方案的直接"幼稚"实现会执行h步贪婪策略改进，然后通过自举"通常"价值函数评估该策略。出乎意料的是，我们发现此过程并不一定会朝着最优价值收敛，并举例说明了它确实不收敛。该收敛因子取决于h和部分评估参数：m步回报以及资格迹λ。即使满足h-贪婪一致性条件，也会发生不收敛。

　　为了解决这个问题，我们提出了一个简单的解决方案，我们在所有算法中都采用了这种解决方案，该解决方案使收敛速度不受m和λ的依赖，并允许本节前面提到的γ^h收敛。让我们将每个状态视为深度为h的树的根。那么我们提出的修复方法如下。与其仅在所有不与根相关的树搜索输出的叶子上备份和消除备份价值，不如重用树搜索副产物并备份根节点的子节点的最优价值。因此，我们没有自举评估阶段的"通常"价值函数，而是自举从h - 1视野最优规划问题获得的最优价值。

　　这项工作的贡献主要是理论上的，但是在第8节中，我们还介绍了toy领域的实验结果。与"幼稚"算法相比，这些实验通过展示我们的增强的更好性能来支持我们的分析。此外，我们在文献中确定了此增强的先前实际用法。在(Baxter, Tridgell, and Weaver, 1999)中，作者提出备份最优树搜索价值作为一种启发式方法。他们将算法命名为TDLeaf(λ)，并展示了其在替代"幼稚"方法方面的出色表现。最近的一项工作(Lai 2015)介绍了一种名为Giraffe的TDLeaf(λ)的深度学习实现。作者在国际象棋游戏上对其进行测试，声称(在出版期间)"这是迄今为止使用端到端机器学习下棋的最成功尝试"。根据上述的理论结果和经验性成功，我们认为从树搜索中备份最优价值应被视为RL实践者的"最优实践"。

2 Preliminaries

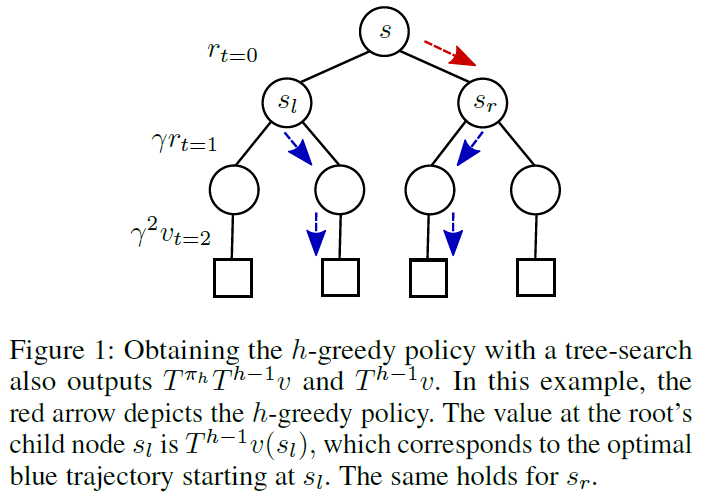
3 The h-Greedy Policy and h-PI

4 h-Greedy Consistency

5 The h-Greedy Policy Alone is Not Sufficient For Partial Evaluation

6 Backup the Tree-Search Byproducts

7 Relation to Existing Work

　　在相关理论工作的背景下，我们发现有两个结果需要讨论。首先是非平稳近似修正PI (NS-AMPI)的性能界限(Lesner and Scherrer 2015)[定理3]。与之相比，定理4表现出两个改进。首先，它使hm-PI对误差的敏感性降低；我们界限的分子用γ^h代替γ。其次，在每次迭代中，hm-PI都需要像NS-AMPI中那样存储单个策略来代替h个策略。这使hm-PI显著提高了内存效率。但是，与(Lesner and Scherrer 2015)相比，我们的工作有一个告诫。在每次迭代中，我们都需要近似求解一个h-有限视野问题，而他们需要求解近似的单步贪婪问题实例。

　　第二个相关的理论结果是最近引入的基于MCTS的RL算法的性能界限(Jiang, Ekwedike, and Liu 2018)[定理1]。该文指出，在无噪声的情况下，无法保证收敛到最优策略¹。相反，在我们的设置中，当δ = 0且ε = 0时，hm-PI和hλ-PI都收敛于最优策略。
　　接下来，我们讨论有关经验研究的相关文献，并尝试用这项工作的结果解释那里的观察结果。在(Baxter, Tridgell, and Weaver 1999; Veness et al. 2009; Lanctot et al. 2014)中，尝试了将树搜索中的最优价值纳入其中的想法。与我们的同步设置最紧密相关的是(Baxter, Tridgell, and Weaver, 1999)。出于实际原因，作者在此介绍并评估了NC hλ-PI和hλ-PI，它们分别称为TD-directed(λ)和TDLeaf(λ)：具体来说，TD-directed(λ)和TDLeaf(λ)分别备份v和。正如注释1所暗示的，可以直接从树搜索中提取，正如在(Baxter, Tridgell, and Weaver 1999)中所指出的。有趣的是，作者表明TDLeaf(λ)优于TD-directed(λ)。确实，定理3阐明了这一现象。

　　最后，定理3和定理4的一个重要启示是AlphaGoZero (Silver et al. 2017b; Silver et al. 2017a)有可能得到改进。这是因为在(Silver et al. 2017b)中，作者没有备份从树搜索中计算出的最优价值。由于他们的方法依赖于PI(特别是类似于h-PI)，因此即使在AlphaGoZero的实际设置中，我们的分析(包括带噪的部分评估)也可能是有益的。

8 Experiments

　　在本节中，我们将在精确和近似的情况下对NC-hm-PI(第5节)和hm-PI(第6节)进行经验性研究。额外结果也可以在附录G中找到。即使在此处考虑的简单设置中，我们的实验也证明了定理3和4的实用性。

　　正如(Efroni et al. 2018a)所做的那样，我们对一个简单的N x N的确定性网格世界问题进行仿真(γ = 0.97)。动作集为{"上"，"下"，"右"，"左"，"停留"}。在每个实验中，将奖励r_g = 1置于随机状态，而在所有其他状态中，奖励均从[-0.1, 0.1]中均匀抽取。在考虑的问题中，没有终端状态。同样，从N(0, 1)中均匀抽取初始价值函数的条目。我们运行算法并计算对仿真器的调用总数。每个此类"调用"都将一个状态-动作对(s, a)作为输入，并返回当前奖励和下一个(确定性)状态。因此，它量化了算法的总运行时间，而不是迭代总数。

　　我们从无噪声的情况开始，其中算法2中的ε_k和δ_k为0。在改变h和m的同时，我们计算直到收敛为止对仿真器的查询总数，其定义为。图3显示了结果。热图在其第一行给出h和m相等范围的收敛时间。它强调了与hm-PI相比NC-hm-PI的次优性。如预期的那样，对于h = 1，NC-hm-PI和hm-PI的结果是一致的，因为这两种算法是等效的。当h > 1时，与hm-PI相比，NC-hm-PI的性能会显著降低一个数量级。但是，随着m的增加，两者之间的差距变得不那么明显。这可以用定理3来解释：增加NC-hm-PI中的m会使(8)中的γ^m急剧收缩，并使收敛因子更接近γ^h，即hm-PI中的那样。在极限m → ∞时，两种算法都成为h-PI。

　　图3的底部行以1-d曲线形式描绘了几个小的h值和很大的m范围的收敛时间。它突出显示了选择m时的折衷。随着h的增加，m的最优选择也增加。对于m与h的折衷进行进一步的严格分析是未来工作的一个有趣的主题。

　　接下来，我们在存在评估噪声的情况下测试了NC-hm-PI和hm-PI的性能。具体来说，。对于NC-hm-PI，根据添加噪声，而不是根据(7)中的第一个公式进行更新。δ_k = 0对应于可以访问精确模型。通常，人们可以利用该模型获得完整的即时解决方案，而不是使用算法2，但在这里我们考虑的情况是，例如由于状态空间太大而无法做到这一点。在这种情况下，我们可以近似估计值，并使用多步贪婪算子访问精确模型。实际上，此设置在概念上类似于AlphaGoZero (Silver et al. 2017b)中采用的设置。图4显示了结果。热图值为，其中π_f是在4 · 10⁶次向仿真器查询后算法的输出策略。随着h的增加，NC-hm-PI和hm-PI都收敛到更好的价值。但是，与前者相比，后者的效果更强，特别是对于较小的m值。 这表明hm-PI对近似误差的敏感性较低。此行为对应于定理4中的hm-PI误差范围，该误差随着h的增加而减小。

9 Summary and Future Work

　　在这项工作中，我们制定，分析和测试了两种简化h-PI评估阶段的方法——多步贪婪PI方案。第一种方法备份v，第二种方法备份T^h-1v或(请参见备注3)。尽管第一个选项似乎是自然选择，但我们证明了它的性能明显比第二个选项差，尤其是在结合短视野评估(即小m或λ)时。因此，由于h-PI与最先进的RL算法之间的密切关系(例如，(Silver et al. 2017b))，我们相信所提出结果可能会在未来导致更好的算法。

　　尽管我们在第5节中确定了算法的不收敛质，但我们并没有证明它们一定会不收敛。我们认为，对不收敛算法的进一步分析很有趣，特别是考虑到它们在无噪声情况下的经验性收敛行为(请参见第8节，图3)。了解不收敛算法何时运行良好具有价值，因为它们的更新规则比收敛算法更容易实现。
　　综上所述，除了(Efroni et al. 2018a; Efroni et al. 2018b)提出的方法之外，这项工作还强调了基于单步的PI方法和基于多步的PI方法之间的另一个差异。即，基于多步的方法在算法设计中引入了新的自由度：规划副产物的利用。我们认为，揭示更多此类差异并量化其优缺点既有趣，又会产生有意义的算法后果。

A Proof of Lemma 1

B Affinity of T^π and Consequences

C Proof of Proposition 2

D Proof of Theorem 3

E h-Greedy Consistency in Each Iteration

F A Note on the Alternative λ-Return Operator

G More Experimental Results