Policy Iterations for Reinforcement Learning Problems in Continuous Time and Space—Fundamental Theory and Methods

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

[Submitted on 9 May 2017 (v1), last revised 31 Oct 2020 (this version, v2)]

Abstract

　　策略迭代(PI)是策略评估和改进的递归过程，用于解决最优决策/控制问题，换句话说，就是RL问题。PI也是开发RL方法的基础。在本文中，对于连续时间和空间(CTS)中的通用RL框架，我们提出了两种PI方法，分别称为差分PI (DPI)和积分PI (IPI)及其变体，其中，环境通过常微分方程(ODE)系统建模。所提出的方法继承了经典RL中PI的当前想法和最优控制，并在理论上支持CTS中现有的RL算法：TD学习和基于价值梯度(VGB)的贪婪策略更新。我们还提供案例研究，包括1）折扣RL和2）最优控制任务。基本的数学属性——可容许性，Bellman方程(BE)解的唯一性，单调改进，收敛性和Hamilton-Jacobi-Bellman方程(HJBE)解的最优性——都经过深入研究并根据现有理论，以及通用和案例研究得以提高。最后，使用倒立摆模型以及基于模型和部分无模型的实现对提出的模型进行仿真，以支持该理论并进一步研究它们。

Key words: policy iteration, reinforcement learning, optimization under uncertainties, continuous time and space, iterative schemes, adaptive systems

1　Introduction

　　策略迭代(PI)是一类近似动态规划(ADP)，用于通过在策略评估之间交替以获得价值函数(VF)来递归解决最优决策/控制问题。当前的策略(又称当前控制理论中的控制方法)和策略改进，通过使用获得的VF对其进行优化来改进策略(Sutton and Barto, 2018; Puterman, 1994; Lewis and Vrabie, 2009)。PI最初是由Howard (1960)在称为Markov决策过程(MDP)的随机环境中提出的，并已成为开发RL方法的基本原理，尤其是在离散时间和空间由MDP建模或近似的环境中。通过有限的MDP的有限时间收敛，已经证明这样的PI向最优解收敛(Puterman, 1994, 定理6.4.2和6.4.6)。与其他ADP方法一样，PI的即时前向计算减轻了被称为维数灾难的问题(Powell, 2007)。折扣因子γ ∈ [0, 1]通常被引入PI和RL，以抑制未来奖励并因此获得有限回报。Sutton and Barto (2018)全面概述了PI和RL算法及其实际应用和最近取得的成功。

　　另一方面，在大多数情况下，实际物理任务的动态不可避免地在连续时间和空间(CTS)中建模为(常)微分方程(ODE)系统。在这种连续域中也主要在确定性最优控制的框架内研究了PI，其中最优解的特征在于偏微分Hamilton-Jacobi-Bellman (HJB)方程(HJBE)。但是，除极少数例外情况外，HJBE很难用解析法解决。该领域中的PI方法通常称为HJBE的逐次逼近(用于递归求解!)，它们之间的主要区别在于其策略评估——较早的PI方法可以解决相关的差分Bellman方程(BE)(又名Lyapunov或Hamiltonian方程)以获取目标策略的每个VF(例如Leake and Liu, 1967; Kleinman, 1968; Saridis and Lee, 1979; Beard, Saridis and Wen, 1997; Abu-Khalaf and Lewis, 2005，仅举几例)。Murray, Cox, Lendaris and Saeks (2002)提出了基于轨迹的策略评估，可以将其视为确定性蒙特卡洛预测(Sutton and Barto, 2018)。受以上两种方法的启发，Vrabie and Lewis (2009)提出了一种部分无模型¹的PI方案，这被称为积分PI (IPI)，该方案与RL更相关，因为相关的BE具有TD形式——参见Lewis and Vrabie (2009)的全面概述。在上面的文献中研究了这些PI的基本数学特性，即策略收敛性，可接纳性和单调改进。结果表明，PI方法生成的策略总是单调地改进并可以接受的。在LQR情况下，由PI方法在CTS中生成的VF序列在二次方收敛到最优解(Kleinman, 1968)。这些基本属性在本文中以包括RL和CTS中的最优控制问题在内的通用设置进行了讨论，改进和推广。

　　另一方面，上述CTS中的PI方法都是通过Lyapunov稳定性理论(Khalil, 2002)设计的，以确保所生成的策略都渐近地稳定动态并产生有限回报(至少在平衡状态附近的有限区域上)，前提是最初的策略也是如此。在此，初始策略下的动态需要渐近稳定才能运行PI方法，但是，这对于IPI来说是非常矛盾的——它是部分无模型的，但是如果没有这种策略，很难找到甚至无法实现这种稳定策略而不需要了解动态。此外，与CTS中的RL问题相比(例如Doya, 2000; Mehta and Meyn, 2009; Frémaux, Sprekeler, and Gerstner, 2013)，基于稳定性的方法限制了折扣因子γ和动态的类别和成本(即奖励)如下。

1. 折扣后，折扣因子γ ∈ (0, 1)必须大于某个阈值，以保持目标最优策略的渐近稳定性(Gaitsgory, Grune, and Thatcher, 2015; Modares, Lewis, and Jiang, 2016)。如果不是，则没有必要考虑稳定性：即使PI收敛且初始策略稳定，PI最终也会收敛到(可能)不稳定的最优解决方案。此外，γ上的阈值取决于动态性(和成本)，因此无法在不了解动态的情况下计算阈值，这与使用任何(部分)无模型方法(如IPI)相矛盾。由于这些γ上的限制，上述用于非线性最优控制的PI方法着重于没有折扣因子(而不是折扣后的)的问题。
2. 在最优规则的情况下，(i) 假定动态具有至少一个平衡状态；² (ii) 目标是针对该平衡状态优化系统，尽管可能会出现分叉或多个孤立的平衡状态；(iii) 为了获得最优的稳定，成本被设计为(半)正定的——当感兴趣的平衡状态转换为零而没有通用性损失时(Khalil, 2002)。最优跟踪问题也存在类似的限制，可以转化为等效的最优调节问题(例如，参见Modares and Lewis, 2014)。

　　在本文中，我们考虑了CTS中的通用RL框架，其中施加了合理的最小假设——1）状态轨迹的全局存在和唯一性；2）(必要时)连续性，可微性和/或函数的最大值的存在，以及3）没有对折扣因子γ ∈ (0, 1]进行假设——包括各种各样的问题。本文中的RL问题不仅包含RL文献中的那些问题(例如，Doya, 2000; Mehta and Meyn, 2009; Frémaux et al., 2013)，但也考虑了稳定框架(至少在理论上)以外的情况，在这种情况下，状态轨迹仍可能受到限制甚至分散(命题2.2; §5.4; 附录§§第31-34页的G.2和G.3)也包括RL和最优控制文献中作为特殊情况出现的输入受限和无约束问题。

　　独立于PI的研究，基于离散域中的RL想法，在CTS中提出几种RL方法。优势更新是由Baird III (1993)提出，然后由Doya (2000)在ODE系统所代表的环境下重新制定的；另请参阅Tallec, Blier, and Ollivier (2019)最近对使用深度神经网络进行的优势更新的扩展。Doya (2000)也将TD(λ)扩展到CTS域，然后将其与他提出的策略改进方法(例如基于价值梯度(VGB)的贪婪策略更新)结合起来。另请参阅Frémaux et al. (2013)对Doya (2000)的连续actor-critic (SNN)拓展。Mehta and Meyn (2009)提出基于随机逼近的CTS中的Q学习。但是，与MDP不同，由于最优控制和RL之间的差距，这些RL方法很少与CTS中的PI方法相关——所提出的PI方法通过与CTS中的TD学习和VGB贪婪策略更新的直接联系弥合了这种差距(Doya, 2000; Frémaux et al., 2013)。对于其他RL方法的ADP的调查仍将作为未来工作或参见我们的初步结果(Lee and Sutton, 2017)。

¹ 本文中的"部分无模型"一词意味着可以使用(1)中动态 f 的一些部分知识(即输入耦合项)来实现该算法。

² 有关没有平衡状态的动态的示例，请参见(Haddad and Chellaboina, 2008, 示例2.2)。

1.1　Main Contributions

　　本文的主要目标是在时域和状态-动作空间都是连续的且具有ODE模型系统建模环境的情况下，从经典RL和最优控制的PI想法出发，在通用RL框架中建立PI理论。作为结果，一系列PI方法被提出，从理论上支持CTS中的现有RL方法：TD学习和VGB贪婪策略更新。我们的主要贡献概述如下。

1. 受PI方法进行最优控制的启发，对于我们的通用RL框架，我们提出了基于模型的PI(称为差分PI (DPI))和部分无模型的PI (IPI)。所提出的方案不一定需要运行初始稳定策略，而可以认为是CTS中的一种基本PI方法。
2. 通过同时包含折扣RL和最优控制框架的案例研究，所提出的PI方法和理论变得简化，改进，且专用，与RL和CTS中的最优控制有很强的联系。
3. 关于PI(和ADP)的基本数学属性——可容许性，BE解的唯一性，单调改进，收敛和HJBE解的最优性——以及通用和案例研究都进行了深入研究。最优控制案例研究还检查了PI的稳定性。作为结果，最优控制中PI的现有属性得以改进并得到严格的泛化。

　　我们还提供了倒立摆模型的仿真结果，并提供了基于模型的和部分无模型的实现，以支持该理论，并在可接受的(但不一定稳定)初始策略下(与"bang-bang控制"和"带有简单二值奖励的RL"有强烈的联系)进一步研究了所提出的方法，这两者都超出了我们的理论范围。在此，本文中的RL问题是自由稳定的(在最小假设下定义明确)，因此(初始)可接纳策略在理论和提出的PI解决方法中不一定是稳定的。

1.2　Organizations

　　本文的组织如下。在§2中，我们制定了CTS中的通用RL问题以及与BE，策略改进和HJBE有关的数学背景，符号和陈述。在§3中，我们介绍并讨论了两种主要的PI方法(即DPI和IPI)及其变体，它们与CTS中的现有RL方法紧密相关。我们在§4中展示了所提出的PI方法的基本属性：可容许性，BE解决方案的唯一性，单调改进，收敛性以及HJBE解决方案的最优性。通过以下案例研究，对§4中的这些属性以及§2和4中的假设进行了简化，改进和放松：1）凹Hamiltonian公式(第5.1节)；2）有限VF/奖励(第5.2节)的折扣RL；3）局部Lipschitzness的RL问题(第5.3节)；4）非线性最优控制(§5.4)。在§6中，我们讨论并提供了主要PI方法的仿真结果。最后，结论在§7中得出。

　　我们单独提供附录(请参阅下面的第19页及其后部分)，其中包含符号和术语(§A)的摘要，相关工作和重点(§B)，有关理论和实现的细节(§§C–E和H)，无法控制的示例(§F)，其他案例研究(§G)和所有证据(§I)。在整篇论文中，任何以上述字母开头的部分都将在附录中指明一个部分。

1.3 Notations and Terminologies

　　以下注释和术语将在整篇文章中使用(有关注释和术语的完整列表，包括未在下面列出的，请参阅§A)。在任何陈述中，iff 和 s.t. 分别代表"当且仅当"和"使得 ... 满足 ... "。表示根据定义正确的等式关系。

2　Preliminaries

³ 如果初始时间t₀不为零，则继续进行时间变量t' = t - t₀，该变量在初始时间t = t₀时满足t' = 0。

2.1　RL problem in Continuous Time and Space

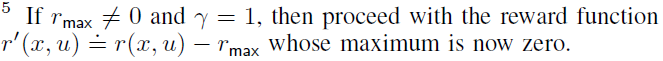
2.2　Bellman Equations with Boundary Condition

2.3　Policy Improvement

2.4　Hamilton-Jacobi-Bellman Equation (HJBE)

3　Policy Iterations

　　现在，我们准备陈述两个主要的PI方案，即DPI和IPI。在此，前者是基于模型的方法，而后者是部分无模型的PI。此后还将讨论其离散化的简化版本(部分无模型)。在§6之前，我们以理想的方式介绍和讨论这些PI方案，而无需引入(i) 任何函数近似，例如神经网络，以及(ii) 状态空间中的任何离散化。⁶

⁶ 当我们实现任何一个PI方案时，显然都需要这两个方案(线性二次调节(LQR)情况除外)，因为VF的结构已被遮盖，并且无法对连续状态空间中(不可计数)无限数量的点执行策略评估和改进 (有关实现示例，另请参见§6，详细信息参见§H)。

3.1　Differential Policy Iteration (DPI)

　　我们的第一个PI，称为差分策略迭代(DPI)，是一种基于模型的PI方案，从最优控制扩展到RL框架(例如，参见Leake and Liu, 1967; Beard et al., 1997; Abu-Khalaf and Lewis, 2005)。算法1描述了DPI的整个过程——它从初始的可接受策略π₀(第1行)开始，并执行策略评估和改进，直到v_i和/或π_i收敛(第2-5行)。在策略评估(第3行)中，智能体求解差分BE (19)以获得最近策略π_i-1的VF 。然后，将v_i用于策略改进(第4行)，以便通过最大化(20)中的关联Hamiltonian函数来获得下一个策略π_i。在此，如果v_i = v_*，则根据(17)和(20)，π_i = π_*。

　　基本上，DPI是基于模型的(请参见h的定义(5))，并且不依赖于任何状态轨迹数据。另一方面，其策略评估与CTS中的TD学习方法紧密相关(Doya, 2000; Frémaux et al., 2013)。要看到这一点，请注意关于(X_t, U_t)，(19)可以用表示(对于所有x ∈ X和t ∈ T)，其中 t 表示TD误差，可以被定义为：

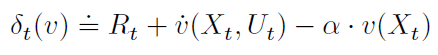
对于任何C¹函数v：X → R。Frémaux et al. (2013)使用SNN将δ_t(v)用作无模型actor-critic的TD误差，并近似v以及δ_t(v)的模型依赖部分δ_t(v)。δ_t(v)也是CTS的TD(0)中的TD误差(Doya, 2000)，其中近似为反向时间中的(对于在时间间隔(0, α^-1)中选择的足够小的时间步骤)；在这种反向时间近似下，δ_t(v)可以类似于离散时间的TD误差的形式表示为：

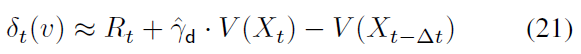
对于和。这里，如果是γ，则折扣因子属于(0, 1)，这要归功于，并且只要γ = 1，。总之，DPI的策略评估解决了差分BE (19)，这理想化了CTS中现有的TD学习方法(Doya, 2000; Frémaux et al., 2013)。

3.2　Integral Policy Iteration (IPI)

　　算法2描述了第二个PI，即积分策略迭代(IPI)，它与DPI的区别在于，用于策略评估和改进的(19)和(20)分别由(22)和(23)代替。除了在主循环之前初始化时间视野η > 0 (第1行)外，其他步骤与DPI相同。

　　在策略评估(第3行)中，对于给定的固定视野η > 0，IPI求解积分BE (22)，而无需使用系统(1)的动态 f 的显式知识——在(22)中没有 f 的显式项，并且对于动态 f 的信息被第 i 次迭代在π_i-1下针对多个初始状态X₀ ∈ X生成的状态轨迹数据{Xt：0 ≤ t ≤ η}隐式捕获。根据定理2.5，对于固定的η > 0求解积分BE (22)及其DPI中的差分形式(19)是等效的(只要v_i满足§4中的边界条件(28))。

　　在策略改进(第4行)中，我们考虑动态 f 的分解(24)：

其中(被称为漂移动态)与动作u独立并假定为未知，并且是先验已知的相应输入-耦合动态；⁷ 假设f_d和f_c都是连续的。由于项对关于u的最大化无贡献，因此可以在分解(24)下将策略改进(14)重写为：

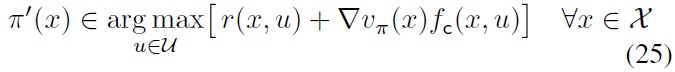
通过它可以直接获得算法2的策略改进(第4行)。请注意，算法2和(25)中的策略改进(23)是部分无模型的——最大值不取决于未知的漂移动态f_d。

　　IPI的策略评估/改进分别是完全无模型/部分无模型的。因此，算法2的整个过程是部分无模型的，即，即使完全不知道漂移动态f_d也可以做到。除了这种部分无模型的属性外，IPI中的视野η > 0可以是任何值——可以大也可以小——只要在实践中近似时累积奖励没有明显的误差即可。从这个意义上讲，时间视野η与离散时间的n步TD预测中的数字n相似(Sutton and Barto, 2018)。实际上，如果对于某些且足够小的，则通过前向时间近似，其中：

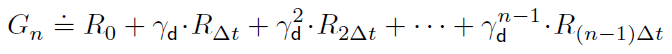
且，则积分BE (22)表示为：

其中。我们还可以应用的高阶近似——例如，在梯形近似下，我们有：

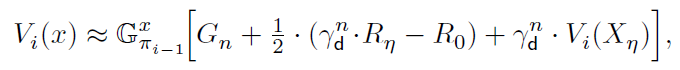
它使用终点奖励R_η，而(26)不使用。注意，对于这样的多步TD预测，TD误差(21)不容易泛化。另一方面，当n = 1时，n步BE (26)变为：

这类似于离散时间的BE (Sutton and Barto, 2018)，CTS中的TD误差(21)的。

⁷ 选择f_d和f_c的方法有无数种；一个典型的选择是f_d(x) = f(x, 0)和f_c(x, u) = f(x, u) - f_d(x)。

3.3　Variants with Time Discretizations

4　Fundamental Properties of Policy Iterations

　　本节显示了DPI和IPI的基本属性——可接受性，每种策略评估解决方案的唯一性，单调改进和收敛(朝着HJB解决方案)。我们还讨论了HJB解决方案的最优性(§§4.2和E.1)基于PI的收敛性。在任何数学陈述中，<v_i>和<π_i>表示BE和策略的解决方案的序列，均由算法1或2在以下条件下生成：

4.1　Convergence towards v_* and π_*

4.2　Optimality of the HJB Solution: Sufficient Conditions

5　Case Studies

　　凭借与RL的紧密联系以及CTS中的最优控制，本节研究§2中提出的通用RL问题的特殊情况。在这些案例研究中，如表1所示，对提出的PI方法和理论进行了简化和改进。表1中的空白用"Assumed"填充，在简化的策略改进部分中用"No"填充。本节还介绍了最优控制中的稳定性理论。在每种情况下，对HJB解的最优性进行了研究，并在§E.2中进行了总结；§G中提供了更多案例研究。

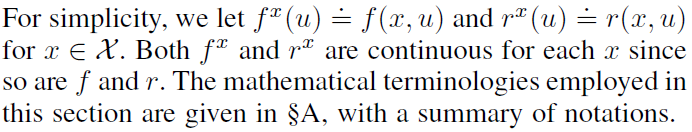
5.1　Concave Hamiltonian Formulations

　　在此，我们研究奖励函数 r 的特殊设置，使函数变得严格凹且为C¹(在非仿射动态的情况下经过一些输入变换后)。在这些情况下，策略改进最大化(13)，(14)和(17)成为凸优化，其解存在并以封闭形式给出，我们将看到这极大地简化了策略改进本身并增强了收敛性。尽管我们专注于某些动态类别(输入仿射动态然后是一类非仿射动态)，但该想法可以扩展到形式为(1)的一般非线性系统(有关此类扩展，请参见第G.1节)。

5.1.1　Case I: Input-affine Dynamics

5.1.2　Case II: a Class of Non-affine Dynamics

5.2　Discounted RL with Bounded VF

5.3　RL with Local Lipschitzness

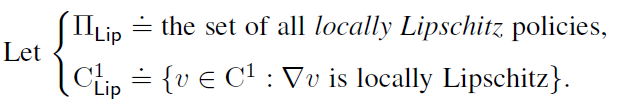
5.4　Nonlinear Optimal Control

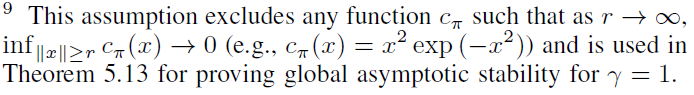
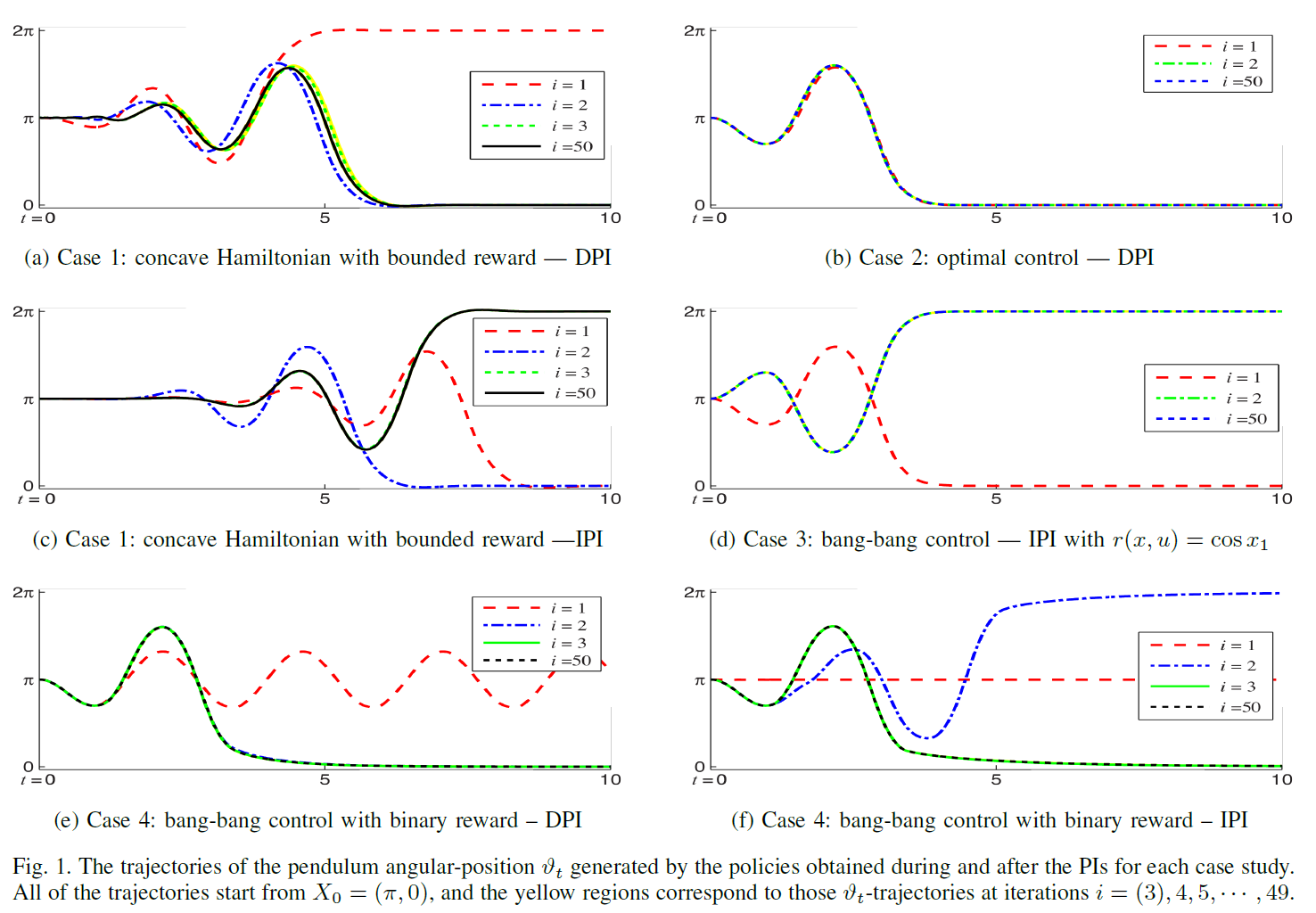
6　Inverted-Pendulum Simulation Examples

¹⁰ github.com/JaeyoungLee-UoA/PIs-for-RL-Problems-in-CTS/

6.1　Case 1: Concave Hamiltonian with Bounded Reward

6.2　Case 2: Optimal Control

6.3　Case 3: Bang-bang Control

6.4　Case 4: Bang-bang Control with Binary Reward

6.5　Discussions

　　我们已经在上述四种情况下仿真了DPI和IPI(算法3)的变体。它们中的一些在第一次迭代时就立即达到了学习目标，并且在所有仿真中，所提出的方法最终都能够达到目标。另一方面，PI的实现存在以下问题。

1. 每个策略评估的最小二乘解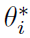都会在有限数量的初始状态下使Bellman误差最小化(如§H中所述)，这意味着在整个区域Ω内最小化Bellman误差不是最优选择。如第3节所述，理想的策略评估无法准确实现——即使Ω是紧凑的，它也是一个连续的空间，因此包含(无数)无限数量的要点，我们在实践中无法完全涵盖。
2. 由于最小平方中的数据矩阵的维数为L x (NM)= 121 x 420 (请参见§H)，因此计算最小二乘解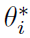的计算量很大，并且数值误差(并因此收敛)对参数的选择(例如特征的数量，时间步骤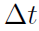，折扣因子γ，当然还有N和M)敏感。在我们的实验中，我们观察到案例2(最优控制)对这些参数最不敏感。
3. VF参数化。由于摆在x₁ = 0处是对称的，因此图2中获得的VF和策略都是对称的，因此大约估计VF
   在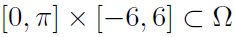就已足够(具有较少的权重)，并且使用问题的对称性。由于过参数化，我们已经观察到，即使在VF V_i几乎收敛之后，权重向量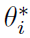在某些情况下也不会收敛，而是在两个值之间振荡。

　　所有这些算法和实际问题均不在本文讨论范围之内，并且仍作为未来的工作。

7　Conclusions

　　本文提出了基本的PI方案DPI(基于模型)和IPI(部分无模型)来解决CTS中制定的通用RL问题，并证明了它们的基本数学属性：可容许性，BE解的唯一性，单调改进，收敛和HJBE解决方案的最优性。通过将所提出的方法作为理想的PI，与CTS中的RL方法(TD学习和VGB贪婪策略更新)建立牢固的联系。案例研究简化并改进所提出的PI方法及其理论，并与RL紧密联系，并在CTS中实现最优控制。使用基于模型和部分无模型的实现方式进行了数值仿真，以支持该理论，并在可接受但不稳定的初始策略下进一步研究所提出的PI方法。与基于稳定性的框架中现有的PI方法不同，运行所提出的方法不一定需要初始稳定策略。我们相信，这项工作为(i) 最优控制中的PI方法和(ii) RL方法提供了理论背景，直觉和改进，这些方法将在将来开发并在CTS领域中进行开发。

Abstract

　　这份补充文件提供了更多的研究内容，以及Lee and Sutton (2020)提出的所有内容细节，如下所列。粗略地说，我们以相同的缩写，术语和符号表示相关的工作，理论，算法和实现的细节，其他案例研究以及所有证明。所有不包含字母的等式，部分，定理，引理等的数量均指主要论文中的数量(Lee and Sutton, 2020)，而任何以字母开头的数字均与本文附录中的相对应。

A　Notations and Terminologies

　　我们提供了主要论文和附录中使用的符号和术语的完整列表。在任何陈述中，iff 和 s.t. 分别代表"当且仅当"和"使得 ... 满足 ... "。表示根据定义正确的等式关系。

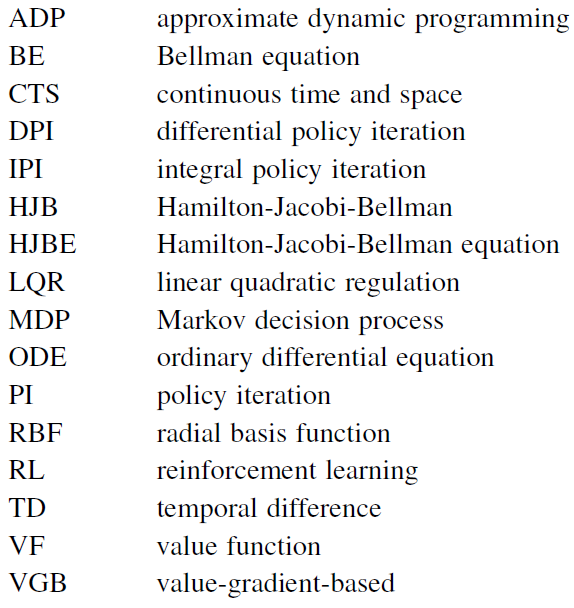
A.1　Abbreviations

A.2　Sets, Vectors, and Matrices

A.3　Euclidean Topology

A.4　Functions, Sequences, and Convergence

A.5　Reinforcement Learning

A.6　Policy Iteration

A.7　Optimal Control and LQRs

B　Highlights and Related Works

　　首先，我们简要回顾一下RL和最优控制领域的相关工作。我们还将重点介绍(i) 由Lee and Sutton (2020)提出的PI方法和基础理论的主要方面，以及(ii) 本文的附录。

DPI & IPI. 我们工作中的两个主要PI方法是DPI，其策略评估与差分BE相关，而IPI与积分BE相关。前者受到最优控制中基于模型的PI方法的启发(例如Rekasius, 1964; Leake and Liu, 1967; Saridis and Lee, 1979; Beard et al., 1997; Abu-Khalaf and Lewis, 2005; Bian et al., 2014)，并与CTS中的TD(0)有直接联系(Doya, 2000; Frémaux et al., 2013)——参见§3.1。关于后者，积分BE最早是由Baird III (1993)在RL领域引入的，然后在最优控制界中受到关注，从而将一系列IPI方法应用于一类输入仿射动态以实现最优规则(Vrabie and Lewis, 2009; Lee et al., 2015)，鲁棒控制(Wang, Li, Liu, and Mu, 2016)和(折扣)LQ跟踪控制(Modares and Lewis, 2014; Zhu, Modares, Peen, Lewis, and Yue, 2015; Modares et al., 2016)，对异策IPI方法进行了许多扩展(例如，Bian et al., 2014; Lee et al., 2015; Wang et al., 2016; Modares et al., 2016)。在我们的工作中(Lee and Sutton, 2020)，

1. 所提出的IPI是由Vrabie and Lewis (2009)给出的第一个IPI激励的，用于非线性最优规则。
2. DPI和IPI的思想已经推广到§2中所示的CTS中的一类广泛的动态和奖励函数，其中包括现有的RL任务(Doya, 2000; Mehta and Meyn, 2009; Frémaux et al., 2013)。§§5和G中介绍了RL和最优控制的案例任务。

Case Studies.

1. (§5.1. Concave Hamiltonian Formulation). §5.1中有一个重点，它描绘了与VGB贪婪策略更新(Doya, 2000)的联系，这是简化输入受限的RL问题中策略改进的总体思路。在输入受限的最优控制领域(Lyashevskiy, 1996; Abu-Khalaf and Lewis, 2005)和无约束的最优规则(Rekasius, 1964; Saridis and Lee, 1979; Beard et al., 1997; Abu-Khalaf and Lewis, 2005; Vrabie and Lewis, 2009; Lee et al., 2015)存在相似的想法(在输入仿射动态甚至非仿射动态下(Bian et al., 2014; Kiumarsi et al., 2016))。
2. (§5.4. Nonlinear Optimal Control). 以上文献以及Leake and Liu (1967)提出的现有最优调节方法PI与§5.4密切相关，在此我们研究了DPI和IPI应用于一般最优调节问题(非仿射动态和γ ∈ (0, 1])的渐近稳定性和基本性质。§5.4中的定理5.13中给出的渐近稳定性条件与Gaitsgory et al. (2015, 假设2.3和3.8)相似并受其启发。
3. (§5.2 Discounted RL with Bounded VF). 另一个亮点是有界奖励函数的折扣RL问题(§5.2)。在这种情况下，可以保证VF不受任何策略的约束，通过该策略，基础的PI理论将得到极大简化和清晰(请参见推论5.9)。该框架类似于有限MDP中的RL任务，其中为每个状态转换定义的奖励是有界的(Sutton and Barto, 2018)。

有关RL和最优控制的§5.1、5.2和5.4中案例研究的仿真示例，另请参见§6。

Admissibility & Asymptotic Stability. 从理论上讲，由于我们考虑了无稳定性的RL框架(在§2中的最小假设下)，因此我们将渐进稳定性排除在可容许性策略的定义之外。在此，最优控制的可容许性概念已被定义为具有渐近稳定性(例如Beard et al., 1997; Abu-Khalaf and Lewis, 2005; Vrabie and Lewis, 2009; Modares and Lewis, 2014; Bian et al., 2014; Lee et al., 2015，仅举几例)，这项工作是第一个在没有渐近稳定性的情况下定义CTS的可容许性的工作。相反，在一般的最优控制问题中，我们还表明，当γ = 1时，根据我们的定义，可容许性表示渐近稳定性(如果关联的VF为C¹)——参见定理5.13和§5.4中的备注5.14和5.20。这意味着即使在最优控制下，渐近稳定性也可以从可容许性的定义中删除。在§5.4中，在比Lyapunov的全局渐近稳定性标准弱的条件下(例如，见定理5.17)，还研究了折扣最优控制的可容许性。

(Mode of) Convergence. 我们通过以下三种方式描述了PI方法向最优解的收敛性。 这三种模式提供了不同的收敛条件并相互补偿。

1. 在第一个表征中，我们采用了Bessaga (1959)的收敛定点原理，证明了PI方法生成的VF在一个度量中收敛到最优值(定理4.5)。这种第一类型的收敛(称为度量收敛)比下面的局部均匀收敛要弱，但是除了固定点的存在和唯一性(推论E.2证明是最优VF)外，没有强加任何其他假设。
2. 第二种方法是扩展Leake and Liu (1967)的方法，表明PI算子的连续性(见定理4.6)是局部一致收敛的额外条件之一。
3. 最后，我们还从最优控制文献(Saridis and Lee, 1979; Beard et al., 1997; Murray et al., 2002; Abu-Khalaf and Lewis, 2005; Bian et al., 2014)中推广了收敛证明。我们的RL框架，在上述两个条件以外的特定条件下，导致三个条件之间最强的融合(请参见定理4.9)。在这个方向上，我们强调指出，为证明第三种类型的收敛性，即使对于最优控制的现有结果，也需要假设由PI获得的VF的梯度在局部均匀收敛，因为生成的VF的收敛性并不意味着它们的导数有任何收敛(见备注5.2)。

LQR. 在§G.3中，我们讨论了DPI和IPI应用于一类LQR任务(Lancaster and Rodman, 1995, 第16章)，其中存在状态和控制的双线性成本项。 在这里，DPI属于现有的一般矩阵形式的PI的特殊情况(Arnold III, 1984; Mehrmann, 1991)，但是这项研究对LQR的许多现有PI方法进行了泛化(例如，Kleinman, 1968; Vrabie et al., 2009; Lee, Park, and Choi, 2014)，并考虑了放宽对一般矩阵形式PI的正定矩阵假设(Mehrmann, 1991, 定理11.3)。

C　More on the Bellman Equations with the Boundary Condition

D Existence and Uniqueness of the Maximal Function u_*

E Theory of Optimality

E.1 Sufficient Conditions for Optimality

E.2 Case Studies of Optimality

F A Pathological Example (Kiumarsi et al., 2016)

G Additional Case Studies

　　本附录提供了与(i) 第5节中的案例研究以及(ii) 主要文章(Lee and Sutton, 2020)和§E中建立的理论(有力的联系)的额外案例研究。

G.1 General Concave Hamiltonian Formulation

G.2 Discounted RL with Bounded State Trajectories

G.3 Linear Quadratic Regulations (LQRs)

 

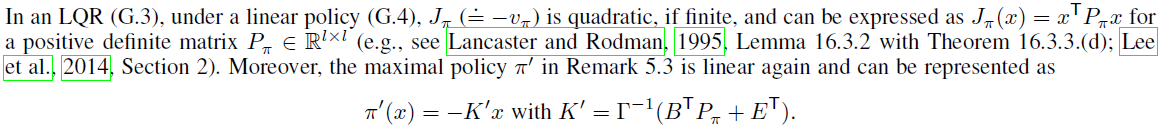
H Implementation Details

　　本附录提供了在§6中实验过的PI方法(即算法3)的实现细节。

H.1 Structure of the VF Approximator V_i

H.2 Least-Squares Solution of Policy Evaluation

H.3 Reward Function and Policy Improvement Update Rule

I Proofs

　　在本附录中，我们提供了主要工作中所陈述的定理，引理，命题和推论的所有证明(Lee and Sutton, 2020)。为了证明局部一致收敛的性质，以下引理是必要的。

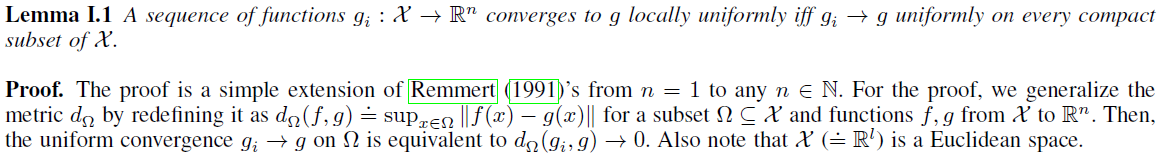
I.1 Proofs in §2 Preliminaries

I.2 Proofs in §4 Fundamental Properties of PIs

I.3 Proofs in §5 Case Studies

 

 

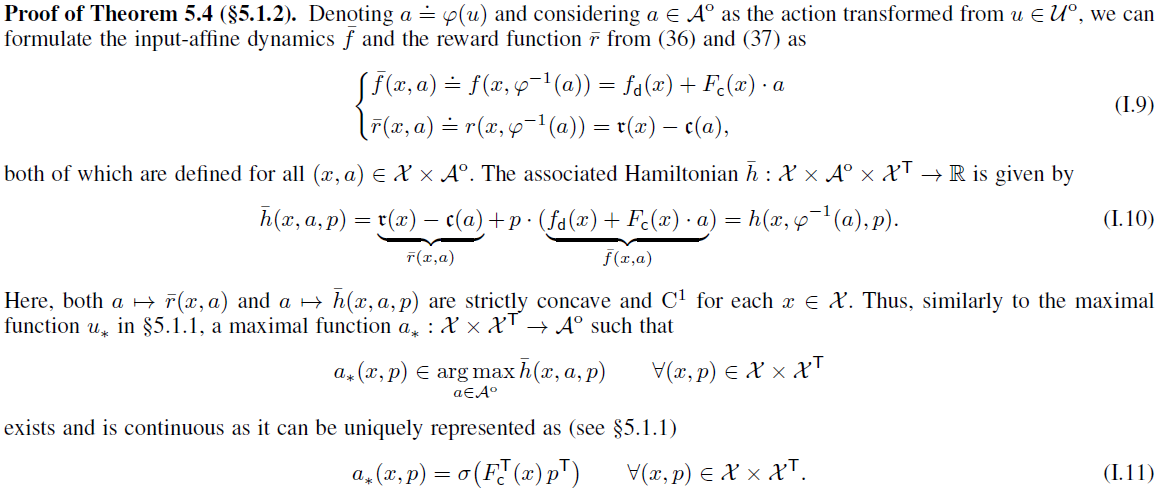
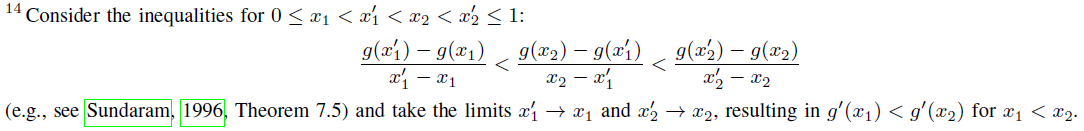
I.4 Proofs of Some Facts in §G.3 LQRs