郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

Neural Comput., no. 4 (2021): 899-925
Abstract
大脑在脉冲神经网络中处理信息。它们错综复杂的连接塑造了这些网络执行的各种功能。相比之下,脉冲网络模型的功能仍处于初级阶段。这个缺点主要是由于缺乏洞察力和实用算法来构建必要的连接。任何此类算法通常尝试通过与所需输出相比迭代地减少误差来构建网络。但是由于脉冲的不可微的非线性,为多层脉冲网络中的隐藏单元分配信度仍然具有挑战性。为了避免这个问题,可以使用替代梯度来发现脉冲网络模型中所需的连接。然而,替代的选择并不是唯一的,这就提出了其实现如何影响方法有效性的问题。在此,我们使用数值模拟来系统地研究替代梯度的基本设计参数如何影响一系列分类问题的学习性能。我们表明替代梯度学习对不同形状的潜在替代导数具有鲁棒性,但导数尺度的选择会显着影响学习性能。当我们将替代梯度与合适的活动正则化技术相结合时,即使在稀疏活动限制下,也可以在脉冲网络中实现鲁棒的信息处理。我们的研究系统地说明了替代梯度学习的显著鲁棒性,并作为功能性脉冲神经网络建模的实用指南。
Introduction
深度神经网络[1, 2]的计算能力重新激发了人们对使用计算机系统研究大脑信息处理的兴趣[3, 4]。例如,性能优化的人工神经网络与视觉系统具有惊人的相似性[5-11],并有助于制定有关其机械基础的假设。同样,为解决认知任务而优化的人工循环神经网络的活动类似于前额叶[12, 13]、内侧额叶[14]和运动区域[15, 16]的皮层活动,并激发了比较和热烈的讨论。
所有这些研究都依赖于机器学习中常用的具有分级激活函数的传统人工神经网络。构建深度神经网络的方法很简单。在网络输出端定义的标量损失函数的值通过梯度下降减少。它们在重要方面不同于生物神经网络。例如,它们缺乏细胞类型的多样性,不遵守戴尔定律,同时忽略了大脑使用脉冲神经元的事实。我们通常接受这些缺陷,因为我们不知道如何构建更复杂的网络。例如,梯度下降仅在涉及的系统可微时才有效。脉冲神经网络(SNN)并非如此。
替代梯度已成为构建能够解决复杂信息处理问题的功能SNN的解决方案[17-24]。为此,出现在梯度解析表达式中的脉冲的实际导数被任何表现良好的函数所取代。这种替代导数有许多可能的选择,因此,与系统的真实梯度不同,所产生的替代梯度不是唯一的。许多研究已经成功地将替代导数的不同实例应用于各种问题集[19, 21, 22, 25-27]。虽然这表明该方法并不主要取决于替代导数的具体选择,但我们对替代梯度的选择如何影响有效性以及某些选择是否比其他选择更好知之甚少。以前的研究没有解决这个问题,因为它们解决了不同的计算问题,因此排除了直接比较。在本文中,我们通过提供用于比较SNN在一系列监督学习任务上的可训练性的基准来解决这个问题,并系统地改变用于在同一任务上训练网络的替代导数的形状和规模。
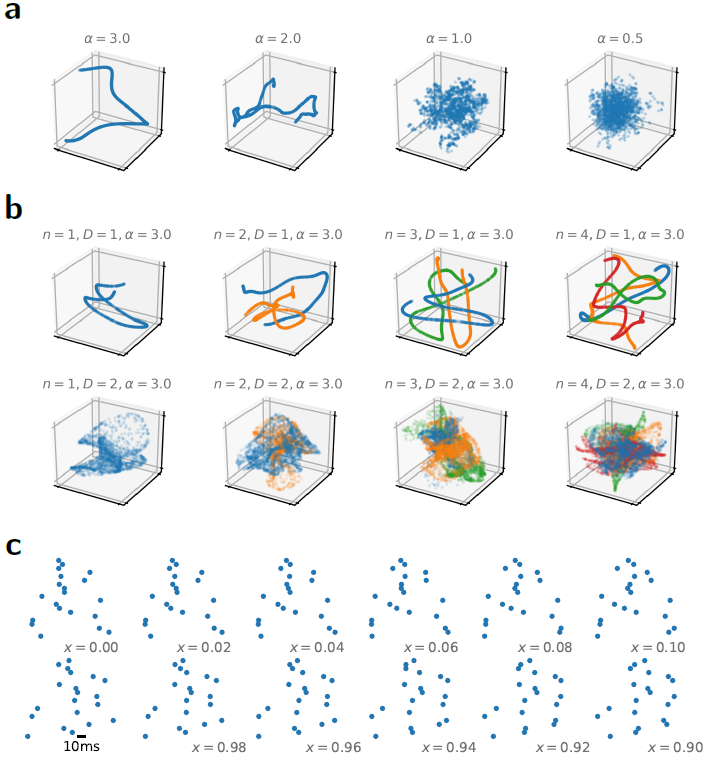
图1. 平滑随机流形提供了一种灵活的方式来生成合成脉冲时序数据集。(a) 四个一维示例流形,用于三维嵌入空间中的不同平滑度参数。从每个流形中,我们绘制了1000个随机数据点。(b) 与 (a) 相同,但在改变流形维数D和随机流形数(不同颜色)时保持α = 3固定。通过对不同的随机流形进行采样,可以直接构建合成的多路分类任务。(c) 对应于沿一维平滑随机流形(α = 3)的固有流形坐标 x 的十二个样本的脉冲光栅图,我们将嵌入空间坐标解释为单个神经元的发放时间。
Results
为了系统地评估替代梯度的性能,我们试图在改变替代梯度的同时针对同一问题重复训练相同的网络。为此,我们需要一个要求苛刻的基于脉冲的分类问题,其计算量很小,以作为基准。SNN的既定基准很少。一种方法是直接使用模拟值机器学习数据集作为输入电流[17]或首先将它们转换为泊松输入脉冲序列[18, 20]。然而,这些输入范式并没有完全利用在脉冲时序中编码信息的能力,这是脉冲处理的一个重要方面。Gütig [28]用Tempotron解决了这一点,通过对随机生成的脉冲时序模式进行分类,其中每个输入神经元发放单个脉冲。然而,完全随机的时间排除了评估泛化性能的可能性,即泛化到以前看不见的输入的能力。为了评估SNN是否可以学习对脉冲模式进行分类并将其推广到不可见模式,我们创建了许多具有添加时间结构的合成分类数据集。具体来说,我们为一组给定的输入传入创建了脉冲栅格。每个传入只发放一个脉冲,所有传入的脉冲时间被限制在所有可能的脉冲时序中的低维平滑随机流形上。来自同一流形的所有数据点都被定义为同一输入类的一部分,而不同的流形对应于不同的类。
脉冲时序流形方法有几个优点:首先,数据中的时间结构允许研究泛化,这是与使用纯随机脉冲模式相比的决定性优势。其次,通过调整传入的数量、流形的平滑度参数(图1a)、固有的流形维度D和类数n (图1b),可以无缝地调整任务复杂性。第三,我们确保每个输入神经元只发放一次(图1c),从而保证生成的数据集完全依赖于脉冲时间,因此无法从发放率信息中分类。最后,从每个类中采样任意数量的数据点在计算上很便宜,并且生成任意数量的具有可比属性的不同数据集同样容易。
为了证明我们的方法的有效性,我们在一个带有单个隐藏层的SNN上测试了一个简单的双向分类问题(图2a; Methods)。我们将隐藏层的单元建模为基于电流的LIF神经元。在层之间,连接是严格的前馈和all-to-all。输出层由两个没有脉冲的泄漏积分器组成,允许我们计算膜电位的最大值[29]并将这些值解释为监督学习(Methods)的标准分类损失函数的输入。在此设置中,具有最高活动水平的读出单元表示每个输入的假定类成员[23]。
当我们使用实际梯度时,我们首先确认学习效果不佳。为此,我们使用脉冲硬阈值非线性的导数来计算它。正如预期的那样,硬阈值非线性阻止了梯度流入隐藏层[24],从而导致性能不佳(图2b, c)。相比之下,当我们使用替代梯度来训练同一个网络时,问题就消失了。学习发生在隐藏层和输出层,导致损失函数大幅减少(图2b-e)。

图2. 替代梯度下降允许构建功能SNN。(a) 顶部有两个读出单元的网络模型草图。(b) 使用实际梯度("true",灰色)或替代梯度(红色)在二元随机流形分类问题上训练SNN时的网络学习曲线。(c) 训练前网络活动的快照。底部:输入层活动的脉冲栅格。对应于两个不同类别的四个不同输入按时间绘制(橙色/蓝色)。中间:隐藏层活动的脉冲栅格。顶部:读出单位膜电位。网络错误地将两个"橙色"输入分类为属于"蓝色"类,这可以从其读出单元的最大活动中读出。(d) 与 c 中相同,但在使用替代梯度下降训练网络之后。(e) 在一次试验中来自7个随机选择的隐藏层神经元的膜电位轨迹示例。
Surrogate gradient learning is robust to the shape of the surrogate derivative
替代梯度学习的一个必要成分是合适的替代导数。为了比较地研究替代导数的影响,我们生成了一个具有十个类的随机流形数据集。我们选择了剩余的参数,即输入单元的数量、流形维数和平滑度,以使没有隐藏层的网络无法解决问题,同时保持最小的计算负担。我们使用快速sigmoid的导数作为替代导数(图3a "SuperSpike"; [25])在这个数据集上训练了具有单个隐藏层(nh = 1)的同一网络的多个实例。在每次运行中,我们保持模型的数据集和初始参数固定,但改变替代的斜率参数β。对于我们对学习率η的每个β值进行参数扫描。训练后,我们测量了保留数据的分类精度。该搜索揭示了系统能够以高精度解决问题的广泛参数机制(图3b)。添加第二个隐藏层仅略微改善了这一结果,而正如预期的那样,没有隐藏层的网络表现不佳(图3c)。产生高性能的参数范围的范围表明,替代梯度学习对替代导数的"陡峭度"变化具有显著的鲁棒性。虽然对阈值的陡峭方法可以被视为更接近,因此更好地逼近脉冲的实际导数,替代梯度在很大程度上不受函数与精确导数的相似程度的影响,只要它不是常数。
接下来,我们测试了不同的替代导数形状,即标准sigmoid (Sigmoid')和分段线性函数(Esser et al.; 图3a; [19, 22])。这种操作导致网络能够执行任务的参数机制的大小减小,这可能是由于梯度消失[30]。然而,最大性能没有显著降低(图3b, c)。使用分段线性替代导数(Esser et al.)导致可行参数的进一步减少(图3b),但不影响最大性能,无论我们使用一个还是两个隐藏层(图3c)。为了检查是否完全需要替代导数来解决随机流形问题,我们分析了β = 0的学习性能,这对应于将函数设置为1。这种变化导致性能显著下降,与没有隐藏单元的网络相比(图3c)表明非线性电压依赖性对于学习有用的隐藏层表示至关重要。最后,我们确认这些发现对于不同的初始网络参数和数据集(图3d)是鲁棒的,除了在两个隐藏层的情况下(nh = 2)只有少数性能低下的异常值。这些异常值指出了正确初始化的重要作用[31, 32]。
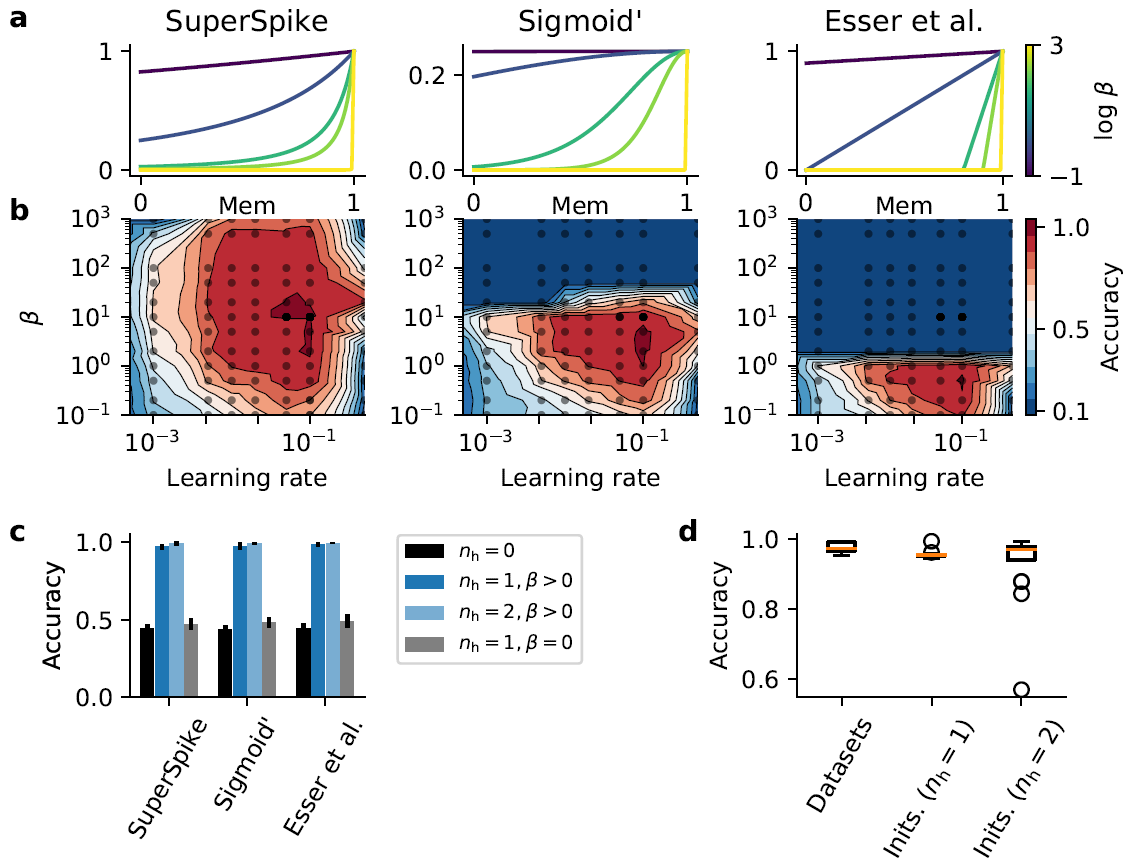
图3. 替代梯度学习对替代导数的形状具有鲁棒性。(a) 三种不同的替代衍生形状,已用于在合成平滑随机流形脉冲数据集上进行训练。从左到右:SuperSpike [25],快速sigmoid函数的导数,Sigma',标准sigmoid函数的导数,以及"Esser et al.",分段线性函数[19, 22]。颜色对应斜率参数β的不同值。(b) 对于具有一个隐藏层(nh = 1)的网络,保留数据的准确性作为学习率和 (a) 中相应替代的斜率的函数。(c) 测试从网格搜索获得的五个最佳参数组合的准确性,如 (b) 所示,对于不同的替代和隐藏层数nh。虽然没有隐藏层的网络无法解决分类问题(黑色),但使用各种不同的替代和斜率参数(β > 0)训练的网络在高精度解决任务(蓝色阴影)方面没有问题。然而,该问题并没有通过具有隐藏层的网络来高精度解决,其中在训练期间替代导数是一个常数(β = 0; 灰色)。误差线对应于标准差(n = 5)。(d) 具有一个隐藏层的网络在随机流形数据集("Datasets")的五种不同实现上的分类准确度的Whisker图,并且对于相同的数据集,但在具有一个(nh = 1)或两个(nh = 2)隐藏层的网络中使用不同的权重初始化("Inits.")。
Surrogate gradient learning in recurrent networks is sensitive to the scale of the surrogate derivative
Surrogate gradient learning is robust to changes in the loss functions, input paradigms, and datasets
Surrogate gradient learning in networks with current-based input
Optimal sparse spiking activity levels in SNNs
Discussion
Methods
Supervised learning tasks
Smooth random manifold datasets
Spike latency MNIST dataset
Auditory datasets
Network models
Neuron model
Readout layer
Connectivity and initialization
Readout heads and supervised loss function
Activity regularization
Surrogate gradient descent