关键词:特征点检测 特征点的性质 Harris角点
作者:李二
日期:23/04/2020 - 27/04/2020
声明:对于大多数做遥感研究的人来说,我觉得没必要深挖里面的技术细节,大致了解一下特征点检测是怎么回事,用到了什么思路即可。如果想看技术细节,自有很多其他博客以及文献可供参考。
我这个人喜欢通过讲解去启发,而不是直接将各位看官带入细节。
李二上次说道:在执行基于图像的三维重建时,要求不同视角的图像能够同时看到地物的相同地方,我们必须在不同图像中精准的找出这些相同的地方,才能够进行三角定位。
1. 再议特征点
一般情况下,不同视角图像中相同的点千千万,都能拿来使用吗?非也!
我们需要从图像中选择比较有代表性的点。套用张麻子一句话,什么TM的是TM的代表性的点?
不妨先看一下图像是个什么东西,图像是一个由亮度和色彩组成的矩阵。我们要从这个矩阵中找出代表性的元素。代表性的点就是相机视角发生变化后,这些点会保持不变,因此这些点是比较特别的点,因此也叫
特征点 feature。
特征点应当具有如下性质:
可重复性(repeatable):相同的特征点可以在不同的图像中找到局部性(localization):特征点仅与一小块图像区域有关可区别性(distinctiveness):不同的特征点有不同的表达高效性(efficiency):同一图像中,特征点数量应远小于像素的数量
那图像中哪些点是特别的点呢?
很容易想到,物体的
角点 corner、边缘点 edge应当具有代表性。我们能够方便的指出,某两幅图像中出现了同一个角点。边缘点则稍微困难一些,毕竟沿着边缘,图像局部是相似的。
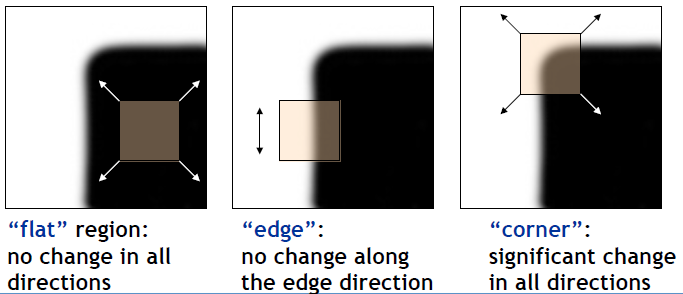
好啦,我们只需要将图像中角点提取出来就好了。目前一般认为角点提取算法的终极算法是Harris角点法,效率最高的算法是FAST角点法(如果需要实时功能的话)。
我们需要思考一下,角点能不能作为稳定的特征点呢? 对于角点,从远处看是角点的地方,近处看可能就不显示为角点了。或者相机或物体旋转后,角点在图像上的外观会发生变化,我看不容易辨认出这是个角点。
(小注:不是说Harris角点不能用,而是一些情况下,不那么好用)
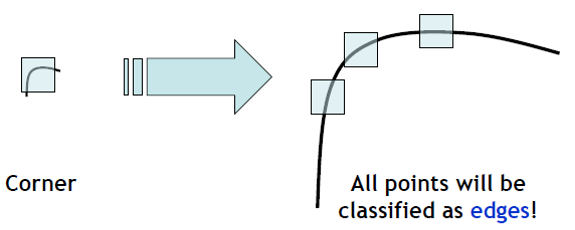
对于特征点,我们追求的一个终极目标是:
敲重点: 不同视角下,物体的光线条件可能不一致,图像的分辨率可能不一致,图像亦可能存在旋转,物体可能存在平移和旋转,因此我们希望这些特征点在几何上能够尺度不变、平移旋转不变,且具有一定的光照不变特点。


2. 特征点检测
接下来,我们一步一步来看看,如何人工设计一些更加稳定的局部图像特征来代替这种普通的角点呢? 我们先从Harris角点入手,然后逐步对其的旋转、尺度等几何不变进行探索。
2.1. Harris角点
2.1.1. Harris的基本思想
以指定大小的滑窗 (locality)为局部特征搜索域,向任意方向移动滑窗,如果均能够得到较大的梯度变化(gradient change),则该滑窗所在中心点即为角点。
我们通过图像中灰度的变化来建模,图像中滑窗 处的灰度矩阵为,滑窗移动后的滑窗的灰度矩阵为,那么灰度的变化为:
这里为
滑窗函数(window function),其实就是一个加权平均,我们可以将滑窗内每个像元的权重设为一致,但更常见的是按照二元Gaussian分布的形式设置权重。
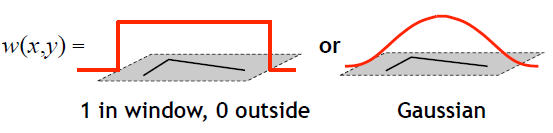
小注:假如窗口中心点是角点时,移动前与移动后,该点的灰度变化应该最为剧烈,所以该点权重系数可以设定大些,表示窗口移动时,该点在灰度变化贡献较大;而离窗口中心(角点)较远的点,这些点的灰度变化几近平缓,这些点的权重系数,可以设定小点,以示该点对灰度变化贡献较小,那么我们自然想到使用二元高斯函数来表示窗口函数,
根据上式,当滑窗在灰度平坦区域上滑动,滑窗灰度矩阵不会发生变化,那么;当滑窗在边缘或角点处滑动,滑窗灰度矩阵变化会很大,那么就很大。
Harris算法核心思想就是计算灰度发生较大变化时所对应的位置,当然这个较大是指针任意方向上的滑动,并非单指某个方向。
2.1.2. Harris的具体理论
接下来对公式(1)进行展开(为什么要展开?容易算呗)。我们对二元函数进行一阶泰勒展开(复习一下去吧),就有:
分别是在轴方向求一阶导。然后就可以把公式(1)写成:
写成矩阵的形式:
(小注,此时不妨假定滑窗内每个像元的权重一致)
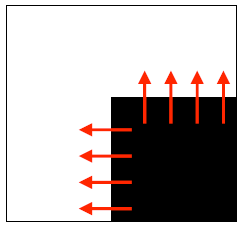
看一个最简单的例子,当角点与 坐标轴对齐时,在下图窗口内(大白格),有一个角点,只有上侧和左侧存在边缘,且在上边缘,很大,而;在左侧边缘,很大而。 所以有
当出现类似这种形式的则意味着:(1)梯度变化主要沿着和轴方向;(2) 如果或者约为0,则这不是一个角点。
实际并非总是如此简单,当角点与 坐标轴没有对齐时,经过旋转变换就可以将其转换到与坐标轴对齐的角度,而这种旋转操作可以使用矩阵的相似化来表示(具体不讲了,因为李二也没想了解)。但无论如何,矩阵是对称矩阵。
来,我们看看,不同情形下,和到底有什么规律。

通过对窗口内的每个像素的方向上的梯度与方向上的梯度进行统计,这里以和为坐标轴,因此每个像素的梯度坐标可以表示成。同时用椭圆进行数据集表示。
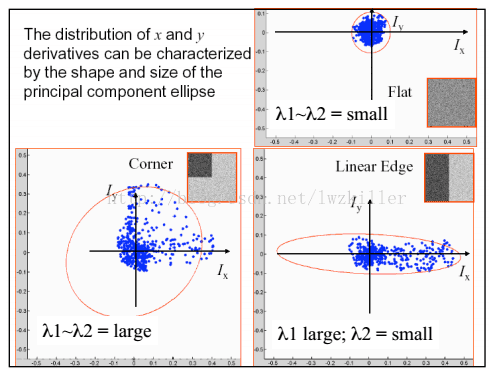
根据这个图我们可以看出:
平坦区域上的每个像素点所对应的坐标分布在原点附近。因为针对平坦区域的像素点,他们的梯度方向虽然各异,但是其幅值都不是很大,所以均聚集在原点附近。矩阵M的对角化的两个特征值比较小.
边缘区域某一坐标轴分布较散,至于是哪一个坐标上的数据分布较散不能一概而论,这要视边缘在图像上的具体位置而定。如果边缘是水平或者垂直方向,那么轴方向或者方向上的数据分布就比较散;矩阵M的对角化的两个特征值理论应该是一个比较大,一个比较小,当然对于边缘这种情况,可能是呈45°的边缘,致使计算出的特征值并不是都特别的大,总之跟含有角点的窗口的分布情况还是不同的.
角点区域的方向上的梯度分布都比较散。矩阵M的对角化的两个特征值都比较大.
(小注:我们对矩阵进行特征值分解)
我们可以根据这些特征来判断哪些区域存在角点,最直观的是下图。虽然我们的基本思想利用
E(u,v)来描述角点,但最终发现仅仅使用的是矩阵M。
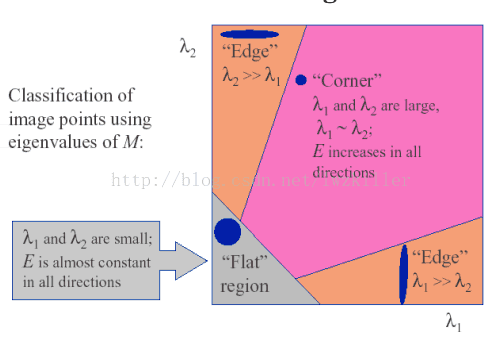
然而矩阵的特征值计算较为复杂,所以使用下面的方法进行近似计算更为高效。即使用
角点响应函数 corner response function
其中为常数,通常为0.04 - 0.06。
刚才用到了权重系数相等的权重函数,现在我们可以用下高斯权重函数(标准正态分布),此时矩阵:
好啦,我们可以用下图总结一下。

如果角点响应函数大于某个阈值,则可以将角点筛选出来。当然其中还可能会有一些后处理步骤,比如说角点的极大值抑制等,就不说了。
2.1.3. Harris角点满足要求吗
我们在section 1中提到了特征点的终极目标是:平移+旋转+尺度+光线变化后,特征点保持不变。那么,Harris角点满足这个需要吗?话不多说,看图便知。
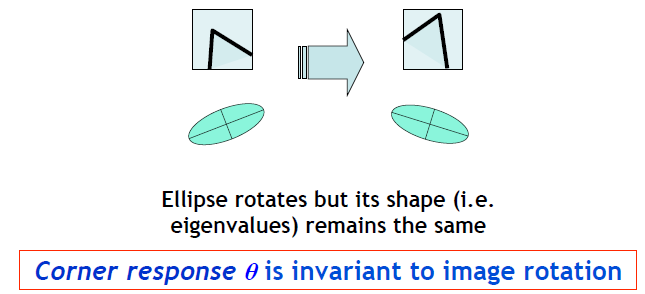

那么,接下来我们看一下,是否能尝试设计出一个尺度不变的特征点检测方法。那就是大名鼎鼎的SIFT。
3. 后记
特征点这块内容有点多,需要3期的内容。因为特征点检测在技术上十分重要,相关算法的一些思路,也极具借鉴价值,所以多写了一些。
特征点,可以用于三维重建(3D reconstruction),也可以用于图像匹配(image matching),我比较建议看一下Stanford University的Fei-Fei Li的CS131中的lec5-7.
有的看官可能觉得人眼应该就可以找出特征点然后进行匹配。好吧,看来是不当家不知炒菜油和洗洁精的区别(嘿嘿,Mme.Zhang),给个例子

啊,竟然还有人能找出来,请收下我的膝盖,这是我职业以来见过最伟大的对眼。再来一发。
