zoukankan      html  css  js  c++  java

  • 速算1/Sqrt(x)背后的数学原理

    概述

            平方根倒数速算法，是用于快速计算1/Sqrt(x)的值的一种算法，在这里x需取符合IEEE 754标准格式的32位正浮点数。让我们先来看这段代码：

     1 float Q_rsqrt( float number )
 2 {
 3     long i;
 4     float x2, y;
 5     const float threehalfs = 1.5F;
 6 
 7     x2 = number * 0.5F;
 8     y  = number;
 9     i  = * ( long * ) &y;                        // evil floating point bit level hacking
10     i  = 0x5f3759df - ( i >> 1 );               // what the fuck?
11     y  = * ( float * ) &i;
12     y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration
13 //    y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed
14 
15 #ifndef Q3_VM
16 #ifdef __linux__
17     assert( !isnan(y) ); // bk010122 - FPE?
18 #endif
19 #endif
20     return y;
21 }

            2010年，John Carmack公开了Quake III Arena的源代码，这段代码便出自其中，这种算法在游戏《雷神之锤III竞技场》（Quake III Arena）被广泛应用，作为《雷神之锤》3D游戏引擎的作者，该算法理所应当的被认为该是Carmark所创，但是后来Carmack在对Beyond3D上关于该段代码的作者的讨论回信表示这段代码并不是出自他之手，也许是其开发小组的另一位成员所写，而至今该算法的最终起源仍然是个谜。

    魔数0x5f3759df

            此算法最为牛叉之处在于注释了what the fuck?的那一行代码，此处将浮点数作为整数右移一位，通过一个神秘的十六进制数0x5f3759df进行减法运算，便完成了牛顿迭代需要的第一次猜测值，而这次猜测值已经很接近满足精度的结果了，因此只通过了一次牛顿迭代就完成了所需精度的结果，其实就相当于直接进行计算就得到了所需结果。

    32位浮点数在计算机中的存储方式

            如果要理解该段代码除了魔数一行的代码，就必须理解浮点数在计算机中的存储方式。任何数据在计算机内存中都是以二进制形式存在的，浮点数也不例外， 32位的浮点数在计算机中的存储方式如下图，分为三个部分：

    1. 标志位（Sign），第31位为标志位，1代表负数，0代表正数；
    2. 指数部分（Exponent），指数部分共占8位，而 float类型规定其偏移量为127，由于指数可正可负，对于8位二进制数其表示范围为[-128, 127]；
    3. 尾数部分（Mantissa），表示有效数字位，由于尾数部分的整数部分恒为1，该位将不被存储，因此原本23位的尾数部分可以表示的精度就变成了24位；

    因此在二进制科学计数法中，我们可以将任意的32位浮点数表示为：

    而平方根倒数速算法中的第9行的目的就是将浮点数转化为32位整型数的表现形式。

    牛顿迭代法

            牛顿迭代法又称为牛顿-拉菲森法（Newton-Raphson method），这种算法的原理就是一个求近似解的方法，该算法正是采用该方法来迭代平方根倒数的。

            要求F(x)=0的解，首先选取一个接近函数F(x)零点的点(x0, F(x0))，过该点做切线求得其与X轴交点的x的值记为x1，该值通常会比x0更接近方程的解，然后不断使用新的点进行迭代至满足的精度为止。

            在(x0, F(x0))点的斜率为，过该点的切线方程为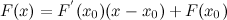，因此求得该切线与x轴的交点横坐标值，因此简化后的迭代公式为：

     以求该平方根倒数求值为例，通过该方法转化为求方程的解，申明，根据牛顿法，第一次迭代结果为：

    而这也正好是算法中的第12行代码对该算法的应用。

    Lomont的逆向数学推理

            对于该算法最让人难以理解的就是魔数0x5f3759df，对于这个问题，Purdue大学的数学家Chris Lomont在论坛上得知后觉得非常有趣，于是决定研究一下它的工作原理。

            Lomont在假设该算法成立的前提下（事实上已被广泛证实该算法的正确性），希望通过数学推理推导出该值。下面简要介绍一下Lomont的推导过程：

            由于是求平方根倒数，因此假设所有浮点数的标志位均为0，浮点数二进制科学计数公式简化为：

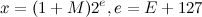    我们假设所求的魔数为R，那么第一次猜测值就可以表示为，其中i表示浮点数x的整数形式，R为整型，如下图：

    在对i进行按位右移的过程中，因为i的二进制指数位可能会被右移到尾数部分，所以必须按两种情况分类讨论：

    1. 当i的指数部分为偶数，那么指数部分的最低位为0，指数位将不会被右移到尾数部分中，而真正的指数e = E - 127就是奇数，令e = 2d + 1，那么在经过运算后，y0的指数部分的值为：

    由于我们所求的平方根倒数大于0，所以新的指数部分也必须大于0，且E的取值在[0, 254]之间，所以R1 ≥ 128；因为E是偶数，所以指数位并没有移动到尾数中，所以运算之后尾数y0的尾数部分为：，

    如果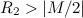，那么初始猜测值为：

    如果，二进制减法正如十进制中的减法运算，需向指数部分借位，此时，

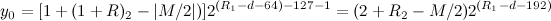
    定义

    那么

    因为e = 2d + 1，那么我们要求解的平方根倒数的近似值为：

    所以y和y0的相对误差则为：

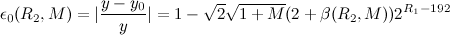
    那么根据要求相对误差需小于0.125，则可以推导出R2的取值范围(189.2, 190.7)，所以R2=190=0xbe；

    2. 当i的指数部分为奇数时，同理推导出：

    如果我们希望以上两种情况的相对误差均小于0.125， R1确定且与E的奇偶无关，那么R1=190=0xbe，此时重新定义以上两个误差函数：

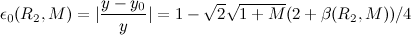
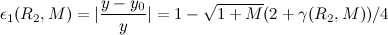
    最终通过当M=0，1，以及R2=M/2的几个临界点获取相对误差最大值函数，然后在所有函数中获取使得这些误差函数值都最小的R2的值，这个值便是我们要找的结果，分类讨论一共得到了9个关于R2(取值范围是[0, 1))的函数：

     

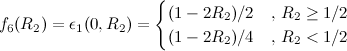
    最终这个求值过程交给Mathematica来完成，也不知为何我最后求得的结果和Lomont略有差异：

    r0 = 0.432744889959443195468521587014

    我求出的结果：

    r0 = 0.432744834277619894180588744347

    其他讨论

            Lomont求解魔数0x5f3759df的推导过程的前提是假设算法中

    i  = 0x5f3759df - ( i >> 1 );

    这行代码成立，通过反推来求解魔数的，但是这行代码最初是如何得出的，依据是什么，Lomont并没有给出更多的解释或猜测，好在其他的论坛也有相关的讨论。

            在一则slashdot.org关于Origin of Quake3's Fast InvSqrt()的讨论中，kent.dickey的回复令人印象深刻，而我个人也非常赞同他的思路，非常简单的推导，也许他的这种思路才是该算法的最初雏形。

            他在回复中说：对于浮点数平方根倒数的求解，指数部分的初始猜测值就是对指数部分减求反（暂时忽略尾数部分，因为对于2以内的求解，一步就可以得到结果），比如求16的平方根倒数：

    但是由于在内存中浮点数特殊的存储方式，因此在内存中指数的整型值为：

    NewExpIntValueInMemory=(ActualExp+127) << 23

    我们想要的指数结果是：

     NewActualExp=-ActualExp/2

    由于在内存中：Exp=ActualExp+127，那么ActualExp=Exp-127，所以：

    NewExp-127=-(Exp-127)/2

    那么：

    NewExp=127-(Exp-127)/2=(127×3)/2-Exp/2

    那 么指数在内存中指数的整型值为：

    所以在完全忽略尾数部分的前提下，初始猜测近似值为：

    i=0x5F400000-i≫1

    随后kent.dickey试图使用类似方法找到对于尾数部分的类似特定模式，遗憾的是没能找到，也许作者当初在有了这个思路（如果该思路真的就是原算法的雏形）之后，也采用了类似Lomont的暴力求解来获得更精确的初始猜测。

    参考文献

    作者：LukyW
    本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利.
  • 相关阅读:
    MySQL的数据库，数据表，数据的操作
    数组函数
    字符串函数，时间函数，数学函数，数组
    PHP函数
    php类型的相关函数，运算符，条件判断，循环
    PHP数据类型
    vector中erase用法注意事项
    C++11 右值引用&&
    vector中find和find_if的用法 以后再遍历剁手！
    在cocos2d中添加自己的shader教程
  • 原文地址：https://www.cnblogs.com/lukyw/p/FastInverseSqrt.html
Copyright © 2011-2022 走看看