线性系统的时域分析方法

第三章 线性系统的时域分析方法

3-1 系统时间响应的性能指标

1. 典型输入信号

2. 动态过程与稳态过程

动态过程：指系统在典型输入信号下，系统输出量从初始状态到最终状态的响应过程。根据系统结构和参数选择情况，动态过程表现为衰减、发散或等幅振荡形式。

稳态过程：系统在典型输入信号下，当时间t趋向于无穷时，系统输出量的表现形式。

3. 动态性能

1. 上升时间：响应从终值10%上升到90%所需的时间；对于有振荡的系统，亦定义为响应从零第一次上升到终值所需要的时间。上升时间越短，响应速度越快。
2. 峰值时间：响应超过其终值到达第一个峰值所需的时间
3. 调节时间：响应到达并保持在终值 $pm$5% 内所需的最短时间
4. 超调量 (sigma\%)：响应的最大偏离量 (c(t_p)) 与终值 (c(infty)) 的差与终值 (c(infty)) 比的百分数。若 (c(t_p)<c(infty))，则响应无超调。

3-2 一阶系统的时域分析

系统对输入信号导数的响应，等于系统对于输入信号响应的导数。

跟踪能力：

时间常数越小，响应速度u越快。

阶跃输入：无稳态误差；斜坡输入：稳态误差等于时间常数T

当传递函数为 (Phi(s) = frac1{Ts+1})时，一阶系统对典型输入信号的输出响应：

输入信号	输出响应
(1(t))	(1-e^{-t/T},quad tge0)
(delta(t))	(frac1Te^{-t/T}quad tge0)
(t)	(t-T+Te^{-t/T}quad tge0)
(frac12t^2)	(frac12t^2-Tt+T^2(1-e^{-t/T})quad tge 0)

3-3 二阶系统的时域分析

标准二阶系统微分方程

[ddot{c}(t)+2zetaomega_ndot c(t) + omega_n^2c(t) = omega_n^2r(t) ]

闭环传递函数

[Phi(s) = frac{omega_n^2}{s^2+2zetaomega_ns+omega_n^2} ]

(omega_n) —— 无阻尼自然振荡频率

(zeta) ——阻尼比（相对阻尼系数）

开环传递函数

[G(s) = frac{omega_n^2}{s(s+2zetaomega_n)} ]

标准二阶系统的特征方程和特征根

令闭环传递函数的分母等于0就得到了标准二阶系统的特征方程

[s^2+2zetaomega_ns+omega_n^2=0 \s_{1,2} = -zetaomega_npmomega_nsqrt{zeta^2-1} ]

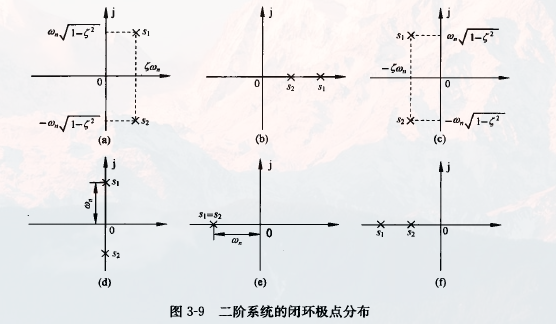
(zeta) 的取值决定特征根在 (s) 平面的位置。

称：

(0<zeta<1) —— 欠阻尼

(zeta = 1) —— 临界阻尼

(zeta > 1) —— 过阻尼

(zeta = 0) —— 无阻尼

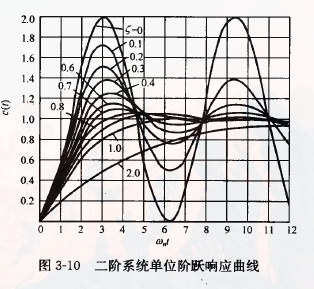
二阶系统单位阶跃响应

1. 欠阻尼的单位阶跃响应

[C(s) = frac{omega_n^2}{s^2+2zetaomega_ns+omega_n^2}cdotfrac1s\ c(t) = 1-frac1{sqrt{1-zeta^2}}e^{-zetaomega_nt}sin(omega_nt+ heta) ]

其中

[ heta = arccoszeta ]

是一个稳态值为1的振荡衰减过程。

2. 无阻尼

[h(t) = 1-cosomega_ntquad tge0 ]

为一个等幅振荡过程。

3. 临界阻尼

[c(t) = 1-e^{-omega_nt}(1+omega_nt)quad tge 0 ]

4. 过阻尼

[c(t) = 1+frac{e^{-t/T_1}}{T_2/T_1-1}+frac{e^{-t/T_2}}{T_1/T_2-1}quad tge0\ T_1=frac1{omega_n(zeta-sqrt{zeta^2-1})}\ T_2=frac1{omega_n(zeta+sqrt{zeta^2-1})} ]

欠阻尼二阶系统的性能分析

上升时间 (t_r)

令 (h(t) =1)得

[t_r = frac{pi- heta}{omega_nsqrt{1-zeta^2}} ]

其中 (omega_d=omega_nsqrt{1-zeta^2}) 被称为阻尼振荡频率。

( heta = arccoszeta) 称为阻尼角。

峰值时间 (t_p)

令 (frac{mathrm dh(t)}{mathrm dt} = 0)得

[t_p = fracpi{omega_nsqrt{1-zeta^2}} ]

超调量

[sigma_p = e^{-pizeta/sqrt{1-zeta^2}} imes100\% ]

调节时间（从振荡开始到回归到一定误差范围内的正常值）

[t_s = frac3{zetaomega_n}(5\%的误差带)\ t_s = frac4{zetaomega_n}(2\%的误差带) ]

延迟时间

[t_d = frac{1+0.7zeta}{omega_n} ]

振荡次数

[N = frac{t_somega_d}{2pi} ]

过阻尼系统的性能分析

上升时间

[t_r =frac{1+1.5zeta+zeta^2}{omega_n} ]

高阶系统的时域分析

当已知高阶系统的各个闭环极点后，可以将其化为以下形式：

[Phi(s) = sum_{j=1}^qfrac{A_j}{s+s_j}+sum_{k=1}^rfrac{B_ks+c_k}{s^2+2zeta_komega_{nk}s+omega_{nk}^2} ]

实部为负的极点

越靠近虚轴，衰减速度越慢，对过渡过程的影响越大。

闭环极点约靠近虚轴，超调量越大；

二阶系统的单位斜坡响应

欠阻尼

[c(t) = t-frac{2zeta}{omega_n}+frac1{omega_nsqrt{1-zeta^2}}e^{-zetaomega_nt}sin(omega_ntsqrt{1-zeta^2}+2arccoszeta) ]

临界阻尼

[c(t) = t-frac2{omega_n}+frac2{omega_n}(1+frac12omega_nt)e^{-omega_nt}quad tge0 ]

过阻尼

[egin{aligned} c(t) = t-frac{2zeta}{omega_n}&+frac{2zeta^2-1+2zetasqrt{zeta^2-1}}{2omega_nsqrt{1-zeta^2}}e^{-(zeta-sqrt{zeta^2-1})omega_nt}\ &-frac{2zeta^2-1-2zetasqrt{zeta^2-1}}{2omega_nsqrt{1-zeta^2}}e^{-(zeta+sqrt{zeta^2-1})omega_nt} end{aligned} ]

稳态分量恒为 (t-frac{2zeta}{omega_n})

二阶系统性能改善

（1）比例-微分控制

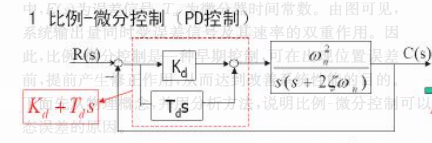
则闭环传递函数变为

[Phi(s) = frac{(T_ds+K_d)omega_n^2}{s^2+(2zetaomega_n+T_domega_n^2)s+omega_n^2} ]

使用比例-微分控制后，既可以减小系统在斜坡输入时的稳态误差，又可以使系统在阶跃输入时有满意的动态性能。

（2）测速反馈控制

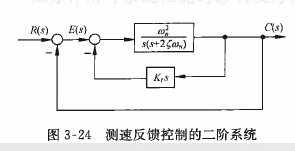
通过将输出的速度信号反馈到输入端，并与误差信号比较，可以增大系统阻尼，改善系统性能。

与微分-控制系统不同的是，测速反馈会降低系统的开环增益，从而加大系统在斜坡输入时的稳态误差。

3-5 线性系统的稳定性分析

稳定性是指系统在受到扰动下偏离原始状态，在扰动消失后恢复到原平衡状态的性能。

如果系统受到扰动后，无论初始偏差有多大，都能恢复到原始平衡状态，则这种系统称为大范围稳定的系统；如果初始偏差只在小于某一范围时才能恢复到初始平衡状态，则称这种系统为小范围平衡的系统。

稳定的充要条件

当且仅当系统的特征根全部具有负实部时，系统才具有稳定性；若有一个正实部根，不稳定；若有一个或一个以上零实部，则具有临界稳定性。

赫尔韦斯判定

劳斯判定

劳斯表的计算：对于上面的那个四元素矩阵：负对角线减去主对角线除以左下角的值。

劳斯判定的特殊情况

1. 劳斯表中的某行的第一列项为零，而其余各项不为零，或不全为零

   可以用因子 ((s+a)) 乘以原特征方程，其中 (a) 为任意正数。

2. 劳斯表中出现全零行

   根据上一行的系数构建一个辅助方程，求导后作为系数写入。

3-6 线性系统的稳态误差计算

[E(s) = R(s) - H(s)C(s) ]

误差的時域表达式为

[e(t) = mathcal{L}^{-1}[E(s)] = mathcal{L}^{-1}[Phi(s)R(s)] ]

如果 (sE(s)) 的极点均位于 (s) 左半平面（包括坐标原点），根据拉氏变换的终值定理，可方便地求出稳态误差

[e_{ss}(infty) = lim_{s ightarrow0}sE(s) = lim_{s ightarrow0}frac{sR(s)}{1+G(s)H(s)} ]

这里要注意拉普拉斯变换终值定理的应用条件：(sE(s)) 的全部极点位于 (s) 平面的左半平面。

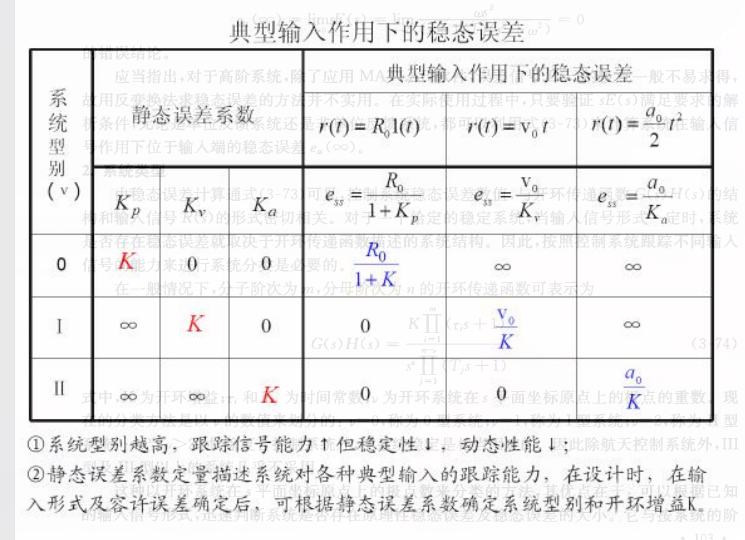
系统类型

在一般情况下，分子阶次为 m, 分母阶次为 n的开环传递函数为

[G(s)H(s) = frac{Kprod_{i=1}^m( au_Is+1)}{s^vprod_{j=1}^{n-v}(T_{jS}+1)} ]

其中 (K) 为开环增益

我们通过 (v) 的数值来称呼相应系统的类型，比如 (v = 0) 就是零型系统，(v=1)就是I型系统。

3-7 扰动作用下的稳态误差

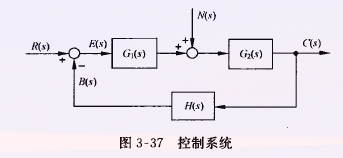
如图为有扰动作用下的信号流图

令输入 (R(s)=0)，得扰动的传递函数

[Phi_n(s) = -frac{G_2}{1+G_1G_2H} ]

扰动输入的稳态误差

[e_{nss} = lim_{s ightarrow0}scdot E_n(s)=lim_{s ightarrow0}scdotPhi_n(s)cdot N(s) ]