一、希尔排序思路

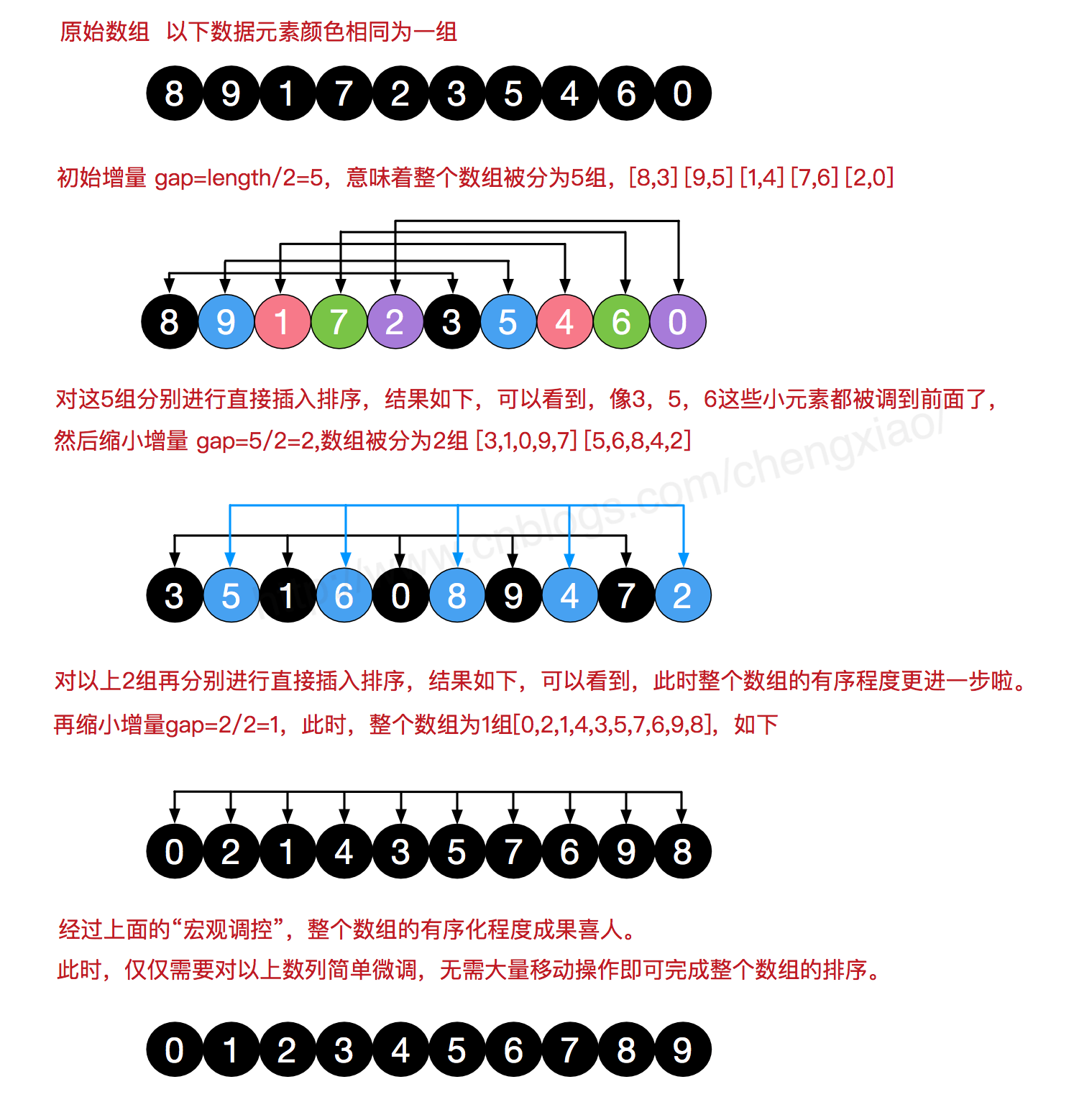
二、图解希尔算法
三、希尔排序代码
def insert_sort(li): for i in range(1, len(li)): #i 表示无序区第一个数 tmp = li[i] #摸到的牌 j = i -1 #j 指向有序区最后位置 while li[j] > tmp and j >= 0: #循环终止条件:1、li[j] <= tmp;2. j== -1 li[j+1] = li[j] j-= 1 li[j+1] = tmp def shell_sort(li): d = len(li) // 2 while d > 0: for i in range(d,len(li)): tmp = li[i] j = i - d while li[j] > tmp and j >=0: li[j + d] = li[j] j -= d li[j + d] = tmp d = d >> 1
四、希尔排序性能分析
1、算法复杂度
会根据增量的不同而不同,一般来说:
时间复杂度:
1. 最好情况:O(n^1.3)
2. 最坏情况:O(n^2)
空间复杂度:O(1)
2、稳定性
稳定性:不稳定(相同元素的相对位置会改变)
希尔排序的时间复杂度讨论比较复杂,并且和选取的gap序列有关
详见官方文档:https://en.wikipedia.org/wiki/Shellsort
五、应用场景
用于大型的数组,希尔排序比插入排序和选择排序要快的多,并且数组越大,优势越大。
六、排序小结
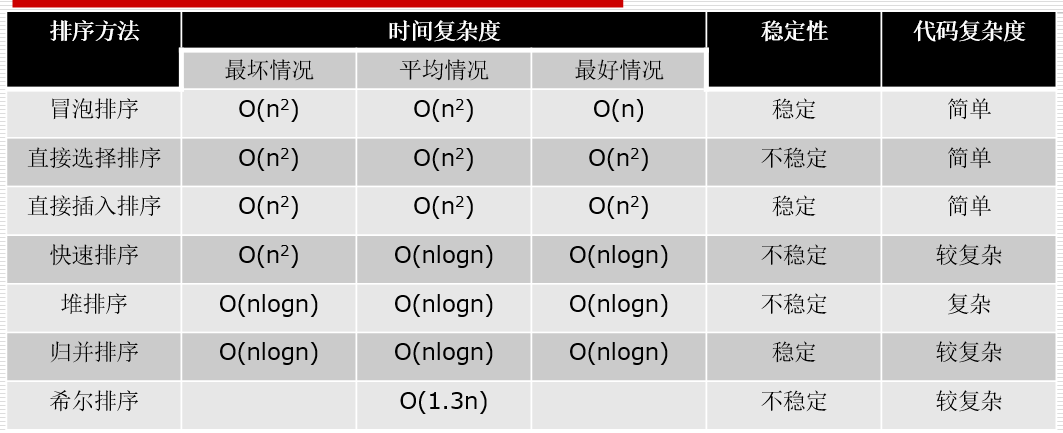
1、小结表
2、什么是算法的稳定性
稳定性是指如果存在多个具有相同排序码的记录,经过排序后,这些记录的相对次序仍然保持不变,则这种排序算法称为稳定的。
比如工资相同的按照年龄排序
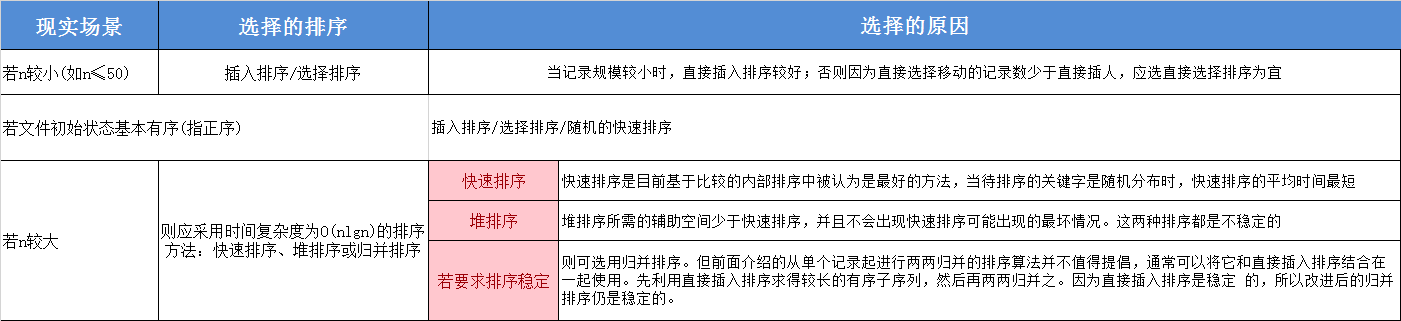
3、应用场景选择