python 为直方图绘制拟合曲线

    def normfun(self, x, mu, sigma):
        """
        正态分布的概率密度函数
        :param x: 数据集中的某一具体测量值
        :param mu: 数据集的平均值，反映测量值分布的集中趋势
        :param sigma: 数据集的标准差，反映测量值分布的分散程度
        :return:
        """
        pdf = np.exp(-((x - mu) ** 2) / (2 * sigma ** 2)) / (sigma * np.sqrt(2 * np.pi))
        return pdf

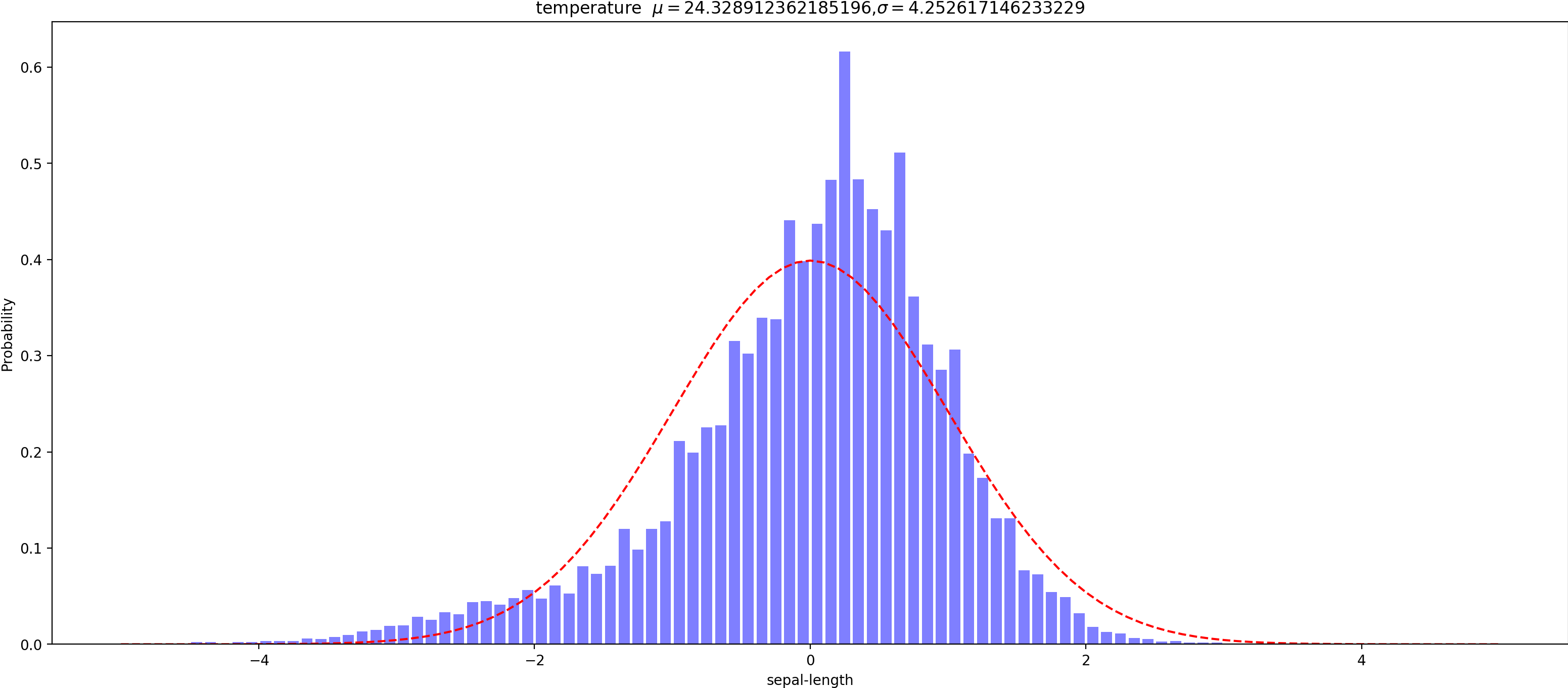
    def draw(self, name, data):
        mean = np.mean(data)  # 计算均值
        std = np.std(data)  # 计算方差
        data1 = [(x-mean)/std for x in data]  # z-score标准化方法(数据标准化)
        num_bins = 100  # 直方图柱子的数量
        plt.figure(figsize=(20, 8))
                            # data数据  num_bins柱子个数 range取值范围[-3.3] rwidth柱子宽度
        n, bins, patches = plt.hist(data1, num_bins, range=[-5, 5], rwidth=0.8, density=0.9, facecolor='blue', alpha=0.5)
        # 直方图函数，x为x轴的值，density=1表示为概率密度，即和为一，绿色方块，色深参数0.5.返回n个概率，直方块左边线的x值，及各个方块对象
        # print(bins)
        y = self.normfun(bins, np.mean(data1), np.std(data1))  # 拟合一条最佳正态分布曲线（方程）y  代替品 ——>>> from scipy.stats import norm  y = norm.pdf(bins, mu, sigma)
        plt.plot(bins, y, 'r--')  # 绘制y的曲线
        plt.xlabel('sepal-length')  # 绘制x轴
        plt.ylabel('Probability')  # 绘制y轴
        plt.title(r'{}  $mu={}$,$sigma={}$'.format(name, mean, std))  # 标题
        plt.subplots_adjust(left=0.15)  # 左边距

        out_file = 'out_pic/%s.png' % name
        plt.savefig(out_file, transparent=True, bbox_inches='tight', dpi=200, pad_inches=0.0, set_visiable=False,
                    format='png')
        print('画图完成 %s' % out_file)
        # plt.show()

 

属性	说明	类型
x	数据	数值类型
bins	条形数	int
color	颜色	"r","g","y","c"
density	是否以密度的形式显示	bool
range	x轴的范围	数值元组（起，终）
bottom	y轴的起始位置	数值类型
histtype	线条的类型	"bar":方形，"barstacked":柱形, "step":"未填充线条" "stepfilled":"填充线条"
align	对齐方式	"left":左，"mid":中间，"right":右
orientation	orientation	"horizontal":水平，"vertical":垂直
log	单位是否以科学计术法	bool

          



参考：计算标准化   https://www.cnblogs.com/yahengwang/p/10634010.html