一 尺度函数与小波函数
基本尺度函数定义为: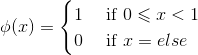 ,对其向右平移任意 k 个单位,构成函数族
,对其向右平移任意 k 个单位,构成函数族 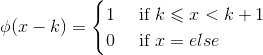 , 该函数族在
, 该函数族在 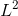 空间中正交,证明如下:
空间中正交,证明如下:
1 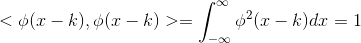 ;
;
2 当 m 不等于 k 时,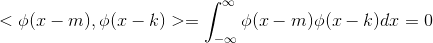
函数族 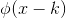 构成一组正交基,并形成
构成一组正交基,并形成  子空间。在
子空间。在  子空间中,任意函数均可表示为
子空间中,任意函数均可表示为  的线性组合,
的线性组合,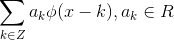 。
。
将函数族  构造宽度缩小一半,则可形成宽度为
构造宽度缩小一半,则可形成宽度为  的一组正交基,
的一组正交基,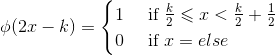 ,同样,该函数族在
,同样,该函数族在 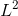 空间中正交,并形成
空间中正交,并形成 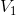 子空间。在
子空间。在 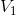 子空间中,任意函数均可表示为
子空间中,任意函数均可表示为 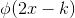 的线性组合,
的线性组合,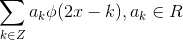 。
。
通过以上举例可得:设 j 为非负整数,j 级函数子空间可表示为 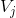 ,其对应正交基包括:
,其对应正交基包括:
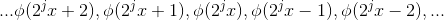 ,观察
,观察 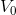 中
中 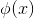 可有
可有 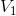 中
中  线性组合(
线性组合(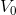 中任意函数均可用
中任意函数均可用 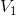 中函数线性组合表达),则
中函数线性组合表达),则 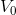 为
为 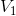 得子空间。各个子空间之间存在如下关系:
得子空间。各个子空间之间存在如下关系: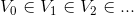 。
。
使用不同子空间 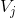 中尺度函数得线性组合,可以阶梯近似任意连续函数。在噪声滤除应用中,需要提取一些属于
中尺度函数得线性组合,可以阶梯近似任意连续函数。在噪声滤除应用中,需要提取一些属于 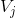 (高频信息)但不属于
(高频信息)但不属于 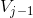 (低频信息)的方法,小波函数即描述了这部分信息,也即小波函数描述
(低频信息)的方法,小波函数即描述了这部分信息,也即小波函数描述  相对于
相对于 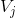 的正交补空间。根据以上描述,小波函数应该满足一些特性:
的正交补空间。根据以上描述,小波函数应该满足一些特性:
1 小波函数仍然位于 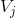 空间中,则他应该是
空间中,则他应该是 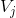 空间基函数的线性组合;
空间基函数的线性组合;
2 小波函数位于 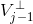 子空间中,则它应于
子空间中,则它应于 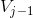 正交。
正交。
 空间的基本小波函数表示为:
空间的基本小波函数表示为: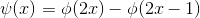 ,该函数位于
,该函数位于 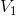 空间,且与
空间,且与 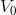 正交。同样对小波函数向右平移 k 个单位,构成函数族:
正交。同样对小波函数向右平移 k 个单位,构成函数族:
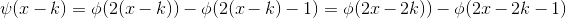 ,该函数族在
,该函数族在 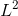 空间中正交。
空间中正交。
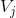 空间的基本小波函数表示为:
空间的基本小波函数表示为: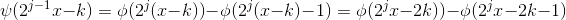 ,该函数族在
,该函数族在 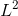 空间中正交。
空间中正交。
使用尺度函数与小波函数,可以将 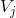 空间中函数进行分解:
空间中函数进行分解: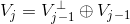 ,其中
,其中 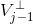 为
为 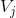 空间中的小波函数,继续以上分解,可得:
空间中的小波函数,继续以上分解,可得:
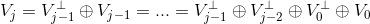
二 Haar分解
1 将函数离散化为 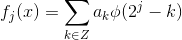 ,该函数位于
,该函数位于 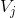 空间中;
空间中;
2 由于 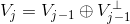 ,可以将
,可以将 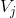 空间中该函数分解为
空间中该函数分解为 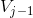 (更平滑尺度函数) 与
(更平滑尺度函数) 与 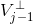 (小波函数),根据尺度函数与小波函数定义,有如下关系:
(小波函数),根据尺度函数与小波函数定义,有如下关系:
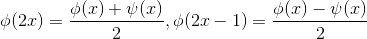 (根据图形可验证结论正确),进一步有:
(根据图形可验证结论正确),进一步有:
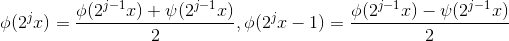 ;
;
3 观察到 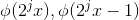 分解方式不一致,需要将原函数改写为:
分解方式不一致,需要将原函数改写为: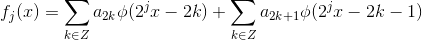 ;
;
4 对改写后的 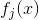 分别使用更平滑尺度函数与对应小波函数再次改写,有:
分别使用更平滑尺度函数与对应小波函数再次改写,有:
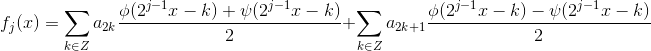 ,整理得:
,整理得:
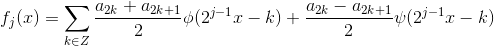 ;
;
5 令 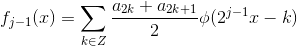 ,继续分解直到
,继续分解直到 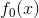 ,可得:
,可得:
 ,其中,
,其中,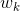 为相应的小波分量。
为相应的小波分量。
三 Haar重构
1 函数被分解为  , 其中,
, 其中,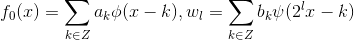 ;
;
2 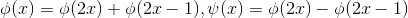 (根据图形可验证结论正确),进一步有:
(根据图形可验证结论正确),进一步有:
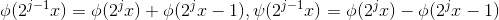
3 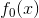 重构为
重构为 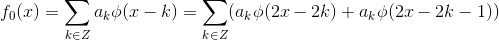 ;
;
4 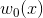 重构为
重构为 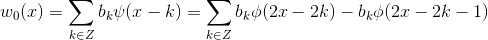 ;
;
5 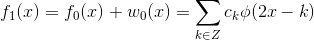 , 其中,
, 其中, 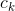 由
由 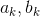 组合;
组合;
6 继续重构 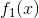 与
与  ,直到重构
,直到重构  。
。
参考资料 小波与傅里叶分析基础 Albert Boggess & Francis J. Narcowich