一 定点整数与定点小数
定点数表示小数点位置固定的数,当小数点放置在最尾部时表示定点整数,当小数点放在在符号位右边时位定点小数。
二进制 0111. 表示定点整数,其十进制值为 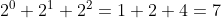 ;
;
二进制 1111. 表示定点整数,其十进制值为 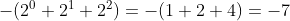 ;
;
二进制 0.111 表示定点小数,其十进制值为 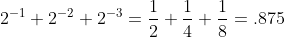 ;
;
二进制 1.111 表示定点小数,其十进制值为 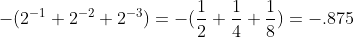 ;
;
以上使用原码表示定点数,在计算机系统中,使用补码表示定点数,这样将减法运算转换为加法运算,具体如下:
原码 0111. 的补码仍然为 0111.,原码 1111. 的补码为 10000. - 0111. = 1001.;
如求十进制数 -7 的补码表示,其步骤如下:
1)求对应正数的补码表示为 0111;
2)对 0111 取反得 1000;
3)对 1000 加 1 得到 -7 的补码表示为 1000 + 1 = 1001;
应用以上规则,可以推导出 7 的补码,其结果与正数补码定义保持一致,如下:
1)对 -7 的补码 1001 取反得 0110;
2)对 0110 加 1 得 0111,结果与正数补码定义保持一致;
针对定点小数,其补码求解方式与定点整数一致,如下:
1)原码1.111 其补码为:0.111 取反得 1.000 加 1 得 1.001;
2)1.001 取反得 0.110 加 1 得 0.111,结果与正数补码保持一致;
当对定点数(定点整数或定点小数)进行加法运算时,如果两个运算数符号不一致(最高位符号),其运算结果不会溢出;如果两个运算数符号一致,当运算结果符号发生改变,则溢出。可以通过比较运算前后符号变化来判断是否溢出,示例如下:
7 + 7 = 0111 + 0111 = 1110,最高位符号发生改变,则溢出。
一个更方便得方法是使用两位符号判断是否溢出,当两位符号不同时,表示溢出;当两位符号相同时,表示无溢出。
二 浮点数表示
浮点数使用科学计数法,将特定长度得连续字节(32位 或者 64位)分割成不同区域,分别表示符号,指数,尾数三个部分,具体如下:
单精度(float) 符号位(1位)+ 指数(8位)+ 尾数(23位)
双精度 (double) 符号位(1位)+ 指数(11位)+ 尾数(52位)
1)符号位使用 0 表示数据为正,使用 1 表示数据为负;
2)尾数一般情况下取值范围为 [1.0, 2),由于整数部分始终为 1 ,故省略掉;
3)指数部分取值范围为 [-126, 127](针对单精度),使用偏置量表示负数,如指数 -1 表示为 -1 + 127 = 126;
下面使用单精度浮点表示 -158.4:
1)正整数部分 158 表示为二进制 1001 1110;
2)小数部分 .4 可表示为 0110 0110 0110 0110...,方法如下:
.4 * 2 = .8 0
.8 * 2 = 1.6 1
.6 * 2 = 1.2 1
.2 * 2 = .4 0
.4 * 2 = .8 0
... ...
3)连接正整数部分与小数部分得 1001 1110. 0110 0110 0110 0110...;
4)规格化尾数得 1.001 1110 0110 0110 0110 0110...,其指数为 0111(十进制数 7);
5)对指数使用偏置得 127 + 7 = 0111 1111 + 0111 = 1000 0110;
7)整合符号位,规格化尾数,偏置后指数得到单精度浮点表示为:1,1000 0110,001 1110 0110 0110 0110 0110;
将单精度浮点数 1,1000 0110,001 1110 0110 0110 0110 0110 转换为10进制得 -158.39990234375,这是浮点运算中误差来源之一。通过使用双精度浮点,可以减小表示误差,但同样无法消除表示误差。计算机表示得浮点数实际上是整个实数集得一个有限子集,双精度只是比单精度能够表示得浮点数更加多一些而已。
三 浮点数误差
浮点数误差来源包括:
1)浮点表示时与真实值之间存在误差,双精度浮点误差小于单精度浮点;
2)浮点数计算时,小阶浮点需要与大阶浮点对阶,右移小阶尾数可能产生舍入误差;
在程序中,应该避免浮点数误差所产生得负面影响。一般策略包括:
1)控制两相加数得阶差,避免舍入误差;
2)必要时使用双精度浮点以减少表示误差;
3)避免双精度浮点转换到单精度浮点所产生的表示误差;
在 float.h 中定义了
#define FLT_EPSILON 1.192092896e-07F // smallest such that 1.0+FLT_EPSILON != 1.0
#define DBL_EPSILON 2.2204460492503131e-016 // smallest such that 1.0+DBL_EPSILON != 1.0
当某个浮点数小于 FLT_EPSILON 或者 DBL_EPSILON 时,该浮点数无法对相加结果产生影响,因此,可以使用该方法来判断浮点相等,如:
if(fabs(num - .1) < FLT_EPSILON) 表示浮点变量 num 与 .1 相等;
当然,由于任意实数被最终转换为一个计算机可表示的浮点值,对于相同转换规则,直接使用 == 判断浮点相等是可行的;在不同硬件体系结构中,是否存在差异,可能需要进一步讨论。