通用的 Blob 检测方法包括:Laplacian of Gaussian(LoG), Difference of Gaussian(DoG), Derterminant of Hessian(DoH)。
opencv 提供了一种简单的方法实现 Blob 检测:SimpleBlobDetector。所谓 Blob,其实就是图像上一些或亮或暗的小连通区域,该连通区域可以使用特定阈值提取出来。
当分析场景相对简单,使用 SimpleBlobDetector 可以比较准确且高效的定位 Blob 区域,基本思路如下:
1 使用连续阈值对图像进行阈值操作,其阈值参数范围为  ,步长为 s;
,步长为 s;
2 使用 suzuki 算法(findContours)提取每个阈值下形成的区域,findContours 得到的每个边界围成的区域被认为是候选 Blob;
使用 findContours 检测连通区域要比连通区域分析算法更加高效,同时,一次 findContours 可以区分内外边界,外边界对应亮区域,内边界对应暗区域,但 opencv 2.4.10 源码中并未对内外边界区分对待;
3 对 Blob 区域进行筛查,筛查条件包括:
1 CV_PROP_RW bool filterByColor; 2 CV_PROP_RW uchar blobColor; 3 4 CV_PROP_RW bool filterByArea; 5 CV_PROP_RW float minArea, maxArea; 6 7 CV_PROP_RW bool filterByCircularity; 8 CV_PROP_RW float minCircularity, maxCircularity; 9 10 CV_PROP_RW bool filterByInertia; 11 CV_PROP_RW float minInertiaRatio, maxInertiaRatio; 12 13 CV_PROP_RW bool filterByConvexity; 14 CV_PROP_RW float minConvexity, maxConvexity;
1)filterByColor 表示提取亮区域或者暗区域。当 blobColor = 255 时,提取亮区域;当 blobColor = 0 时,提取暗区域;
2)filterByArea 表示是否限制 Blob 面积,其面积范围为一个半开半闭区间 [minArea, maxArea);
3)filterByCircularity 表示是否限制 Blob 圆形度,圆形度公式为  。
。
当 Blob 为圆形时,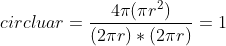 。当 Blob 为一个无限长的椭圆,
。当 Blob 为一个无限长的椭圆, 。故圆形度范围取值范围为 (0, 1];
。故圆形度范围取值范围为 (0, 1];
4)filterByConvexity 表示 Blob 面积与其凸包面积比,取值范围为 (0, 1);
5)filterByInertia 表示 Blob 区域转动惯量最小值与最大值比值,在 “二值图像的几何性质” 博客中,转动惯量表示为:
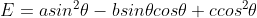 ,
,
 ,
,
 ,
,
 ,
,
由于 转动惯量 E 为一个二次型函数,使用系数矩阵  的特征值与特征向量可描述转动惯量特性,其最小值与最大值比为
的特征值与特征向量可描述转动惯量特性,其最小值与最大值比为 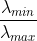 。
。
通过以上分析可知,当 Blob 区域为圆形时,比值接近 1。当 Blob 区域为无限长椭圆时,比值接近 0,故取值范围为 (0,1);
4 对于符合筛查条件的 Blob 区域,使用区域边界到中心点距离中值点作为该 Blob 区域半径;
5 将不同阈值下符合条件的候选 Blob 区域组合到一起,使用 minRepeatability 与 minDistBetweenBlobs 筛查出最终有效 Blob 区域;
以下给出 opencv 对候选 Blob 筛查的部分源码:
1 for (size_t contourIdx = 0; contourIdx < contours.size(); contourIdx++) 2 { 3 4 Center center; 5 center.confidence = 1; // 将可信度置1 6 7 // 求轮廓所围成区域零阶矩,一阶矩,二阶矩,用于筛查条件计算 8 Moments moms = moments(Mat(contours[contourIdx])); 9 10 if (params.filterByArea) 11 { 12 // 零阶矩表示区域面积 13 double area = moms.m00; 14 if (area < params.minArea || area >= params.maxArea) 15 continue; 16 } 17 18 if (params.filterByCircularity) 19 { 20 // 求区域面积与区域周长,并使用圆形度公式计算圆形度 21 double area = moms.m00; 22 double perimeter = arcLength(Mat(contours[contourIdx]), true); 23 double ratio = 4 * CV_PI * area / (perimeter * perimeter); 24 if (ratio < params.minCircularity || ratio >= params.maxCircularity) 25 continue; 26 } 27 28 if (params.filterByInertia) 29 { 30 // 使用二阶矩求区域形状 31 double denominator = sqrt(pow(2 * moms.mu11, 2) + pow(moms.mu20 - moms.mu02, 2)); 32 const double eps = 1e-2; 33 double ratio; 34 if (denominator > eps) 35 { 36 double cosmin = (moms.mu20 - moms.mu02) / denominator; 37 double sinmin = 2 * moms.mu11 / denominator; 38 double cosmax = -cosmin; 39 double sinmax = -sinmin; 40 41 double imin = 0.5 * (moms.mu20 + moms.mu02) - 0.5 * (moms.mu20 - moms.mu02) * cosmin - moms.mu11 * sinmin; 42 double imax = 0.5 * (moms.mu20 + moms.mu02) - 0.5 * (moms.mu20 - moms.mu02) * cosmax - moms.mu11 * sinmax; 43 ratio = imin / imax; 44 } 45 else 46 { 47 ratio = 1; 48 } 49 50 if (ratio < params.minInertiaRatio || ratio >= params.maxInertiaRatio) 51 continue; 52 53 center.confidence = ratio * ratio; 54 } 55 56 if (params.filterByConvexity) 57 { 58 // 求区域面积与凸包面积之比 59 vector < Point > hull; 60 convexHull(Mat(contours[contourIdx]), hull); 61 double area = contourArea(Mat(contours[contourIdx])); 62 double hullArea = contourArea(Mat(hull)); 63 double ratio = area / hullArea; 64 if (ratio < params.minConvexity || ratio >= params.maxConvexity) 65 continue; 66 } 67 68 center.location = Point2d(moms.m10 / moms.m00, moms.m01 / moms.m00); 69 70 if (params.filterByColor) 71 { 72 // 提取亮区域或者暗区域 73 if (binaryImage.at<uchar> (cvRound(center.location.y), cvRound(center.location.x)) != params.blobColor) 74 continue; 75 } 76 77 // 计算 Blob 半径 78 { 79 vector<double> dists; 80 for (size_t pointIdx = 0; pointIdx < contours[contourIdx].size(); pointIdx++) 81 { 82 Point2d pt = contours[contourIdx][pointIdx]; 83 dists.push_back(norm(center.location - pt)); 84 } 85 std::sort(dists.begin(), dists.end()); 86 center.radius = (dists[(dists.size() - 1) / 2] + dists[dists.size() / 2]) / 2.; 87 } 88 89 centers.push_back(center); 90 91 }
参考资料 Learning OpenCV 3 Adrian Kaehler & Gary Bradski