编译原理听课笔记_1
帐户 维唯为为_博客园
正规方法、正规集、正规式
定理1:
1.α+β=β+α
2.α+(β+γ)=α+β+γ
α(βγ)=(αβ)γ
3.α(β+γ)=(αβ)+(αγ)
(α+β)γ=(αγ)+(βγ)
4.εα=αε+α
5.(α*)*=α*
6.α*=α++ε
α+=αα*=α*α
7.(α+β)*=(α*+β*)*=(α*β*)*
定理2:若αβγ是字母表A上的正规式,且ε∈L(γ),则
α=β|αγ,当且仅当α=βγ*
α=β|γα,当且仅当α=γ*β
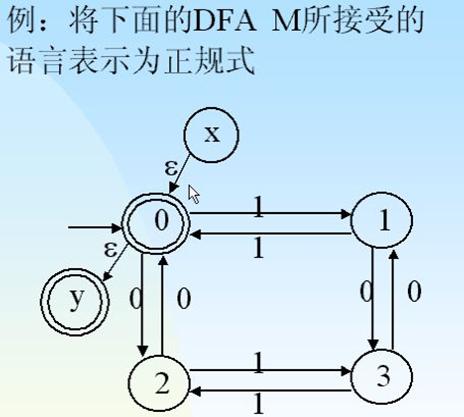
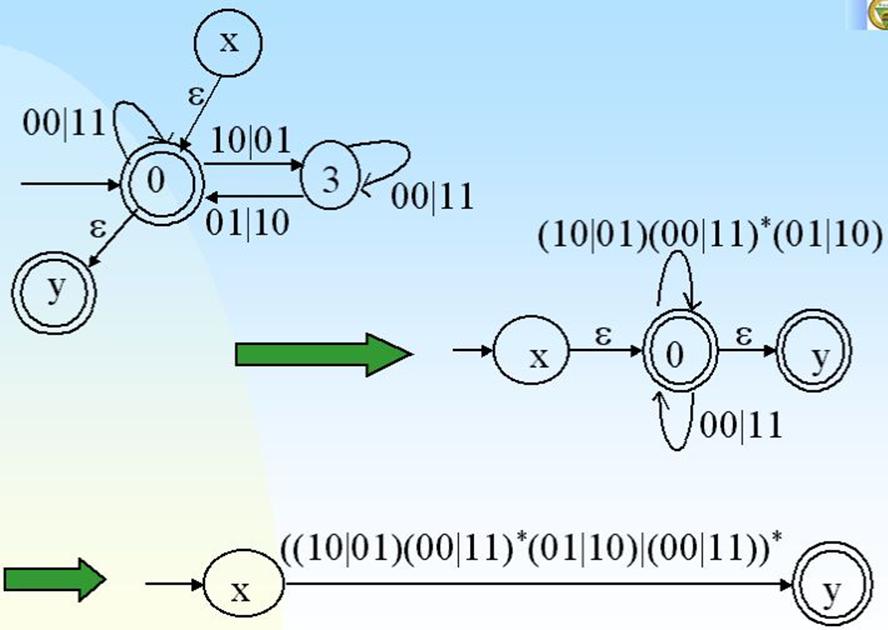
例:已知正规方法G1的产生式,求出它所定义的正规式。
产生式为:
S —> aS|aB
B—> bB|bA
A—> cA|c
解:由产生式写出对应的联立方程组:
S = aS|aB (1)
B= bB|bA (2)
A= cA|c (3) (3)
由(1)式,S(α)=aS(γα) |aB(β) 得:S=a*aB(α=γ*β)=a+B
同理(2) B=bB|bA => B=b+A(=b*bA)
同理(3) A=cA|c => A=c*c=c+
所以,S=a+b+c+
有限自动机(FA finite automata)
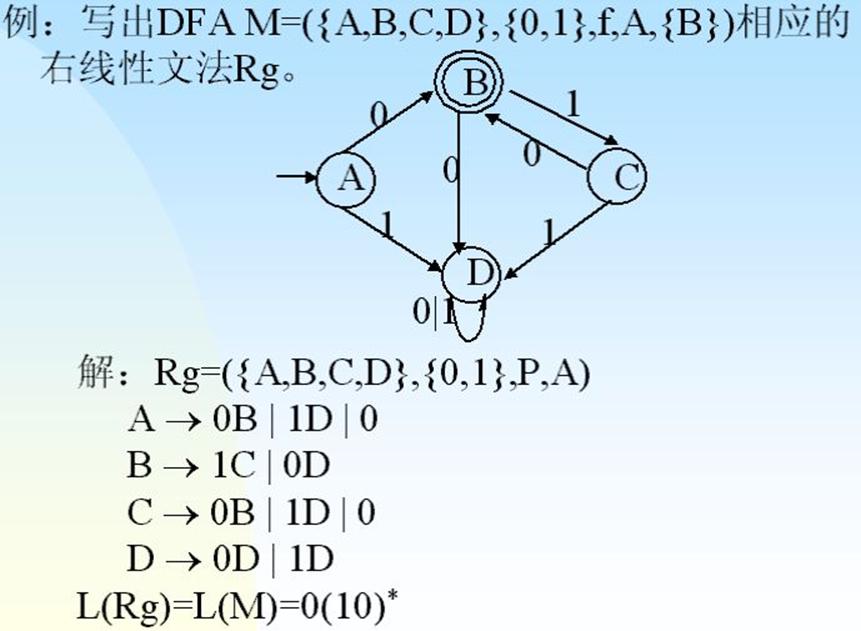
1.确定有限自动机DFA(Determinisic FA)
①它是一个五元式,M(S, Σ, f, S0, Z)
其中S:有限状态集
f:S×Σ—> S上的单值映射,f(S,a)=S'
S0:唯一的初态,S0∈S
Z:终止状态,Z⊆S
②状态转换关系表示:
1.状态转换图矩阵:DFA的映射关系由一个矩阵来表示。
2.状态转换图:
③一步动作
每读入一个字符,状态就向前进至下一状态 ;
记为:"⊦"
⊦k表示自动机做了k步动作。
⊦*表示自动机做了0步动作或0步以上动作。
⊦+表示自动机做了1步动作或1步以上动作。
④DFA对字符串的识别
定义:串 α∈Σ*为DFA M=(S, Σ, f, S0, Z)所识别,当且仅当(S, α) ⊦*(S0, ε),且s∈z
能够被DFA M所接受的字符串的集合,称为自动机M 所能识别的语言,记为L(M)。
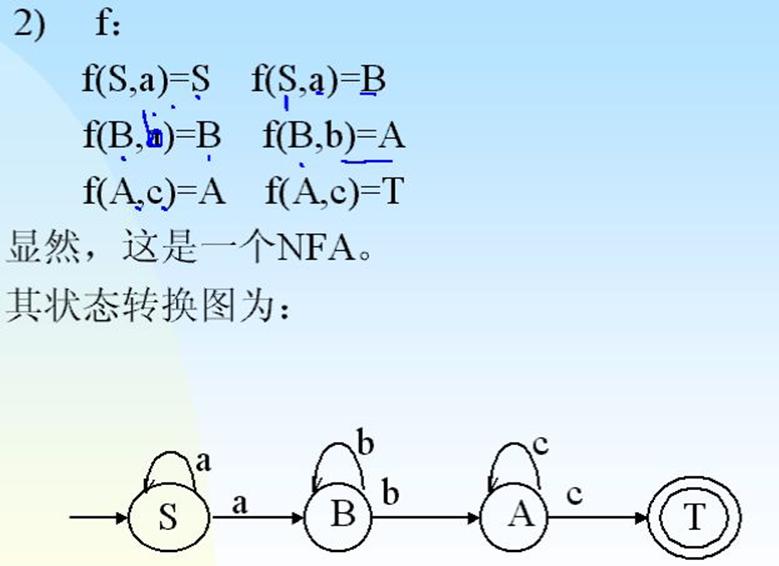
2.不确定的有限自动机NFA(Non-deterministic FA)
①定义:不确定有限自动机是一个五元式, M(S, Σ, f, S0, Z)
其中S:有限状态集
Σ:有限字母表
f:S×Σ—> 2S(S的子集)上的单值映射,f(S,a)=S'
Z:终止状态,Z⊆S,可为空集
②两自动机等价:
对于每个NFA M,存在一个DFA M',使得L(M)=L(M'),即,设L是一NFA接受的正规集,则存在一个DFA接受L 。
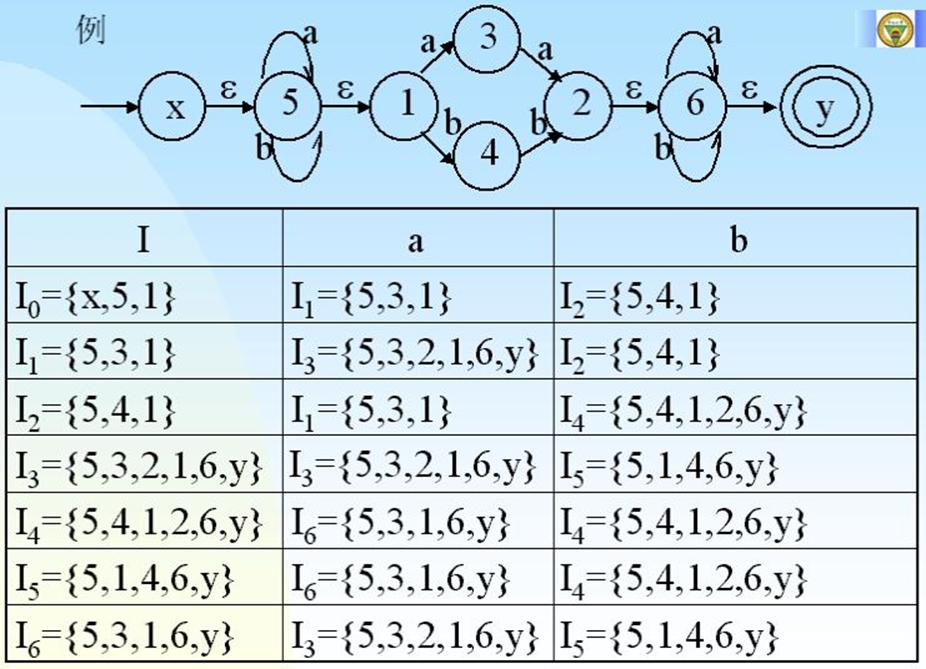
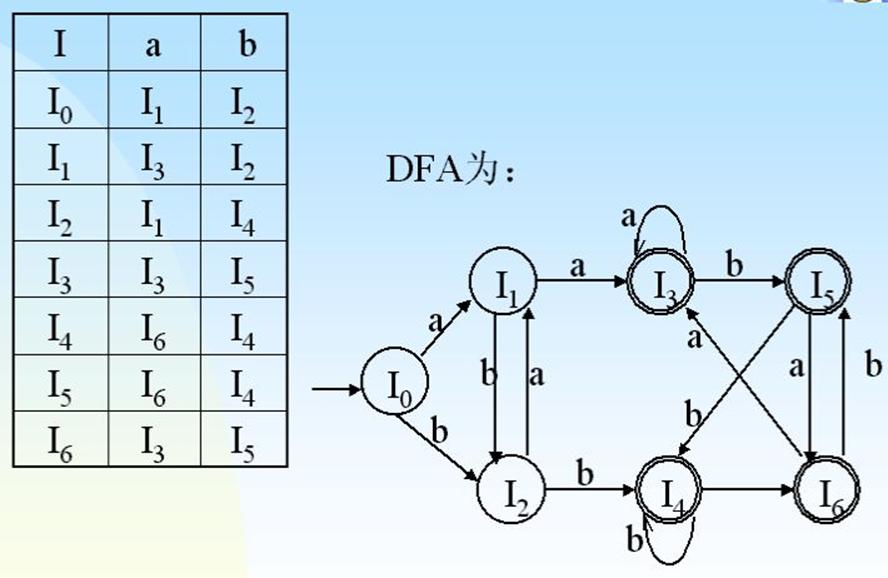
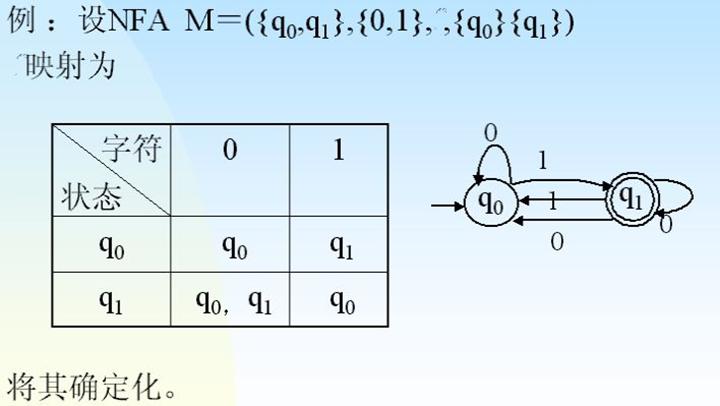
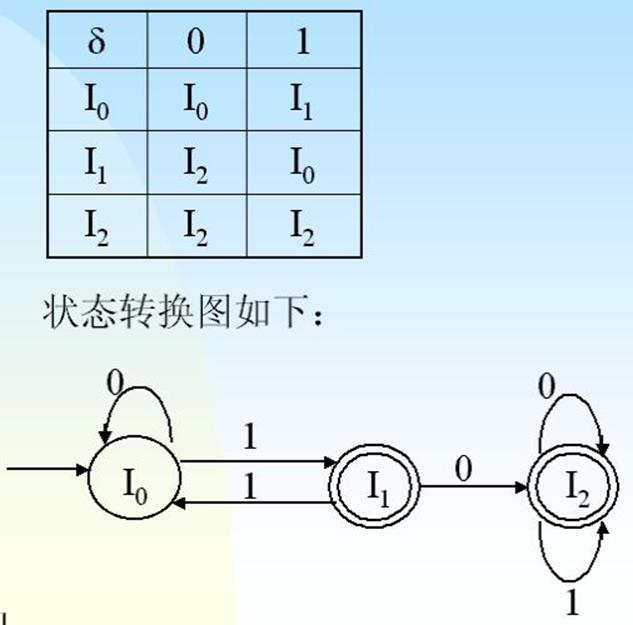
③NFA确定化











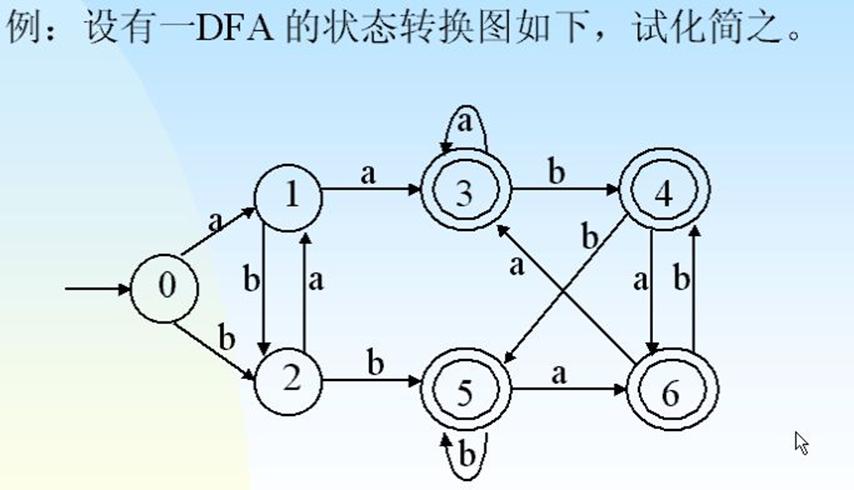


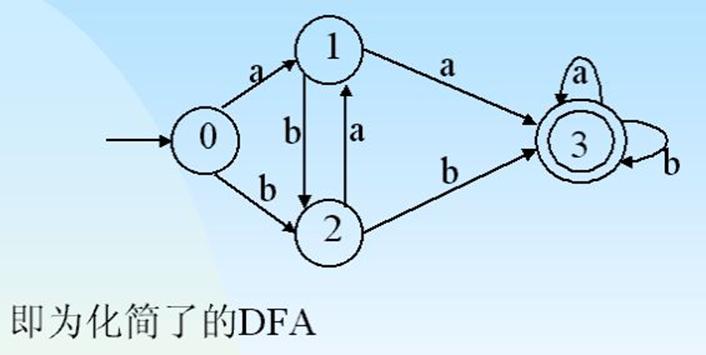
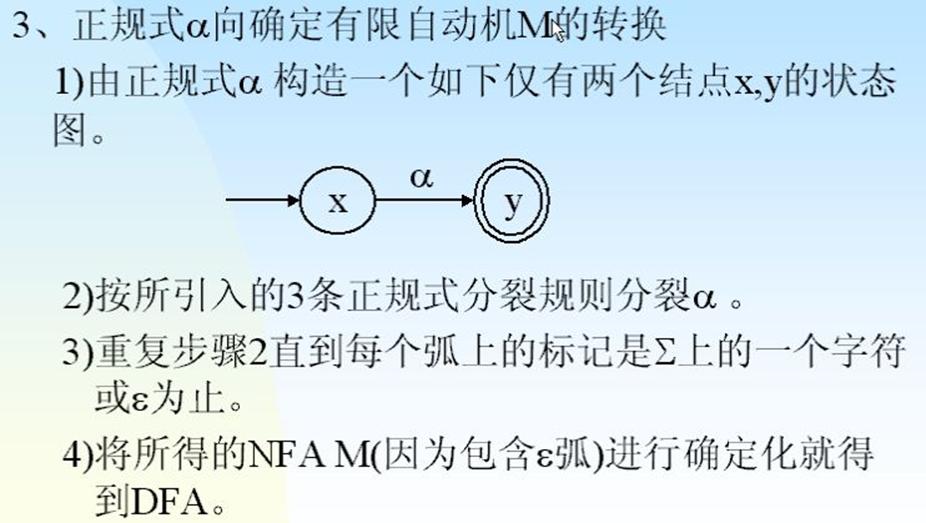
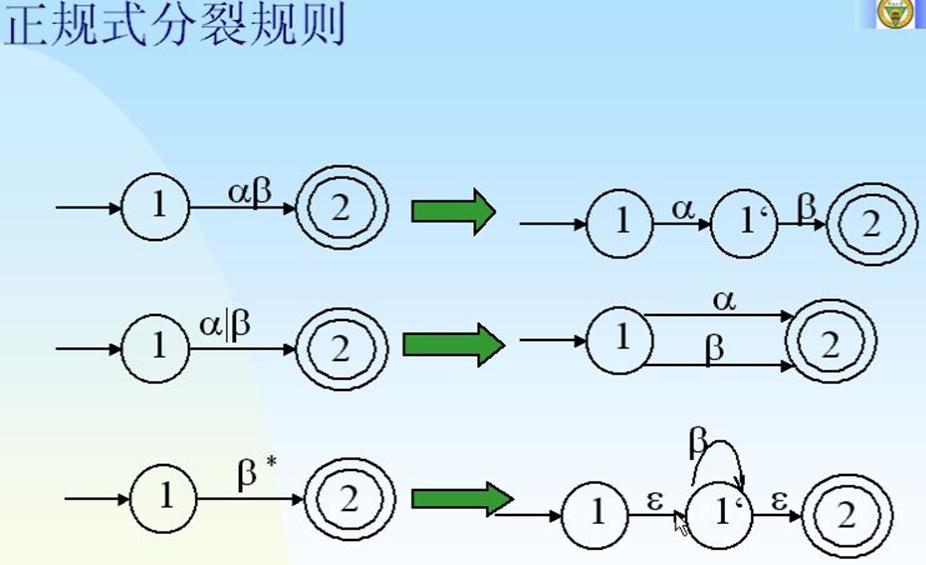
3.正规式与有限自动机之间的关系