本系列文章将于2021年整理出版。前驱教材:《算法竞赛入门到进阶》 清华大学出版社
网购:京东 当当 作者签名书:点我
有建议请加QQ 群:567554289
@
树链剖分是对树的一种巧妙分割。它按一定规则把树“剖分”成一条条线性的不相交的链,并通过DFS序对这些链上的结点重新编号,这些编号具有美妙的特征,能够使用线段树来处理,从而高效地解决一些树上的修改和查询问题。
1. 树链剖分求LCA
首先通过求LCA介绍树链剖分的基本概念。树链剖分的题目也需要用到LCA。
求LCA的各种算法,都是快速往上“跳”到祖先结点。回顾上一节求LCA的两种方法,其思想可以概况为:(1)倍增法,用二进制递增直接往祖先“跳”;(2)Tarjan算法,用并查集合并子树,子树内的结点都指向子树的根,查LCA时,可以从结点直接跳到它所在的子树的根,从而实现了快速跳的目的。
树链剖分也是“跳”到祖先结点,它的跳法比较巧妙。它把树“剖”为从根到叶子的一条条链路,链路之间不相交;每条链上的任意两个相邻结点都是父子关系;每条链路内的结点可以看成一个集合,并以“链头”为集;链路上的结点找LCA时,都指向链头,从而实现快速跳的目的。特别关键的是,从根到叶子只需要经过O(logn)个链,那么从一个结点跳到它的LCA,只需要跳O(logn)个链。
如何把树剖成链,使得从根到叶子经过的链更少?注意每个结点只能属于一个链。很自然的思路是观察树上结点的分布情况,如果选择那些有更多结点的分支建链,链会更长一些,从而使得链的数量更少。
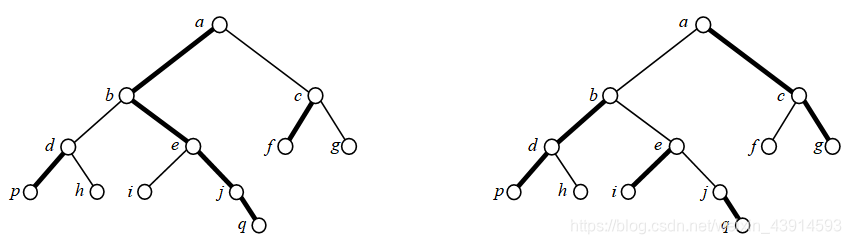
图1(1)从根结点a开始,每次选择有更多子结点的分支建链,最后形成了粗线条所示的3条链。从叶子结点到根,最多经过2条链。例如从h到a,先经过d为头的链,然后就到了a为头的链。
图(2)随意建链,最后得到4条链。从叶子节点到根,最多经过了4条链。例如从q到a,经过了j链、e链、b链、a链。
下面详细解释剖链的过程。图(1)是剖好的链的例子。首先定义以下概念。
重儿子:对一个非叶子结点,它最大的儿子是重儿子。所谓“最大”,是指以这个儿子为根的子树上的结点数量最多(包括这个儿子)。例如,a的重儿子是b,因为以b为根的子树有8个结点,比另一个儿子c大,以c为根的子树只有3个结点。又例如,e的重儿子是j。
轻儿子:除了重儿子以外的儿子。例如a的轻儿子是c,b的轻儿子是d。
重边:连接两个重儿子的边,例如边(a, b)、(b, e)等。定义重边的目的是得到重链。
重链:连续的重边连接而成的链,或者说连续的重儿子形成的链。重链上的任意两个相邻结点都是父子关系。例如a、b、e、j、q形成了一条重链。每一条重链以轻儿子为起点。可以把单独的叶子结点看成一条重链,例如h。
轻边:除重边以外的边。任意两个重链之间由一条轻边连接。
链头:一条重链上深度最小的点。链头是一个轻儿子。如果把一条重链看成一个集合,链头就是这个集合的集。设top[x]是结点x所在重链的链头,图(1)中例如:top[e] = top[j] = a,top[f] = top[c] = c。
利用以上定义剖好的链,最关键的一个性质是:从任意一个点出发,到根结点的路径上经过的重链不会超过 logn条。由于每两条重链之间是一个轻边,也可以这样说:经过的轻边不会超过logn条。
下面证明经过的轻边不会超过logn条。以二叉树为例,x的一个轻儿子y,y 的子树大小必然小于x的子树大小的一半。从根结点往任意一个结点走,设size为当前结点的子树大小,那么每经过一条轻边,size至少除以2。所以最后到达叶子结点时,最多经过了 logn 条轻边。如果是多叉树,每经过一条轻边,size减少得更快,经过的轻边也少于logn个。
经过剖分得到重链之后,如何求两个结点x、y的LCA(x, y)?分析两种情况:
(1)x、y位于同一条重链上。重链上的结点都是祖先和后代的关系,设y的深度比x浅,那么LCA(x, y) = y。
(2)x、y位于不同的重链上。让x和y沿着重链往上跳,直到位于同一条重链为止。重链的定义可以保证x、y最后能到达同一条重链。
例如图(1)中,求p、q的LCA(p, q)。先从p开始跳,跳到链头top[p] = d,然后穿过轻边(b, d)到达上一个重链的结点b,此时发现top[b] = top[q] = a,说明b、q在同一跳重链上,由于b的深度比q浅,得LCA[b, q] = b。注意不能先从q开始跳,请分析原因。
仍然以上一篇的模板题“洛谷P3379”为例给出树链剖分求LCA的代码,代码的主体是三个函数。
(1)dfs1()。在树上做一次DFS求以下数组。
deep[]:deep[x]是结点x的深度。
fa[]:fa[x]是结点x的父结点。当需要穿过一条轻边时,跳到链头的父结点即可。
siz[]:siz[x]是结点x为根的的子树上结点的数量;
son[]:son[x]是非叶子结点x的重儿子。
(2)dfs2()。在树上做一次DFS计算top[],top[x]是结点x所在重链的链头
(3)LCA()。
复杂度:dfs1()和dfs2()都只遍历树的每个结点1次,是O(n)的;LCA()查询一次是O(logn)的,m次查询为O(mlogn)。树链剖分的复杂度和倍增法的复杂度差不多,略好一点。
//洛谷P3379 的树链剖分代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=500005;
struct Edge{int to, next;}edge[2*maxn]; //链式前向星
int head[2*maxn], cnt;
void init(){ //链式前向星:初始化
for(int i=0;i<2*maxn;++i){ edge[i].next = -1; head[i] = -1; }
cnt = 0;
}
void addedge(int u,int v){ //链式前向星:加边
edge[cnt].to = v; edge[cnt].next = head[u]; head[u] = cnt++;
}//以上是链式前向星
int deep[maxn],siz[maxn],son[maxn],top[maxn],fa[maxn];
void dfs1(int x, int father){
deep[x]=deep[father]+1; //深度:比父结点深度多1
fa[x]=father; //标记x的父亲
siz[x]=1; //标记每个结点的子树大小(包括自己)
for(int i=head[x];~i;i=edge[i].next){
int y=edge[i].to;
if(y!=father){ //邻居:除了父亲,都是孩子
fa[y]=x;
dfs1(y,x);
siz[x] += siz[y]; //回溯后,把x的儿子数加到x身上
if(!son[x] || siz[son[x]]<siz[y]) //标记每个非叶子结点的重儿子
son[x]=y; //x的重儿子是y
}
}
}
void dfs2(int x,int topx){
//id[x] = ++num; //对每个结点新编号,在下一小节用到
top[x]=topx; //x所在链的链头
if(!son[x]) return; //x是叶子,没有儿子,返回
dfs2(son[x],topx); //先dfs重儿子,所有重儿子的链头都是topx
for(int i=head[x];~i;i=edge[i].next){ //再dfs轻儿子
int y=edge[i].to;
if(y!=fa[x] && y!=son[x])
dfs2(y,y); //每一个轻儿子都有一条以它为链头的重链
}
}
int LCA(int x, int y){
while(top[x]!=top[y]){ //持续往上跳,直到若x和y属于同一条重链
if(deep[top[x]] < deep[top[y]])
swap(x,y); //让x是链头更深的重链
x = fa[top[x]]; //x穿过轻边,跳到上一条重链
}
return deep[x]<deep[y]?x:y;
}
int main(){
init();
int n,m,root; scanf("%d%d%d",&n,&m,&root);
for(int i=1;i<n;i++){
int u,v; scanf("%d%d",&u,&v);
addedge(u,v); addedge(v,u);
}
dfs1(root,0);
dfs2(root,root);
while(m--){
int a,b; scanf("%d%d",&a,&b);
printf("%d
", LCA(a,b));
}
}
2. 树链剖分的典型应用
上面介绍了树链剖分的概念和简单应用。
关于重链,还有一个重要特征没有提到:一条重链内部结点的DFS序是连续的。这个特征使得可以用数据结构(一般是线段树)来维护重链,从而高效率地解决一些树上的问题,例如以下问题:
(1)修改点x到点y的路径上各点的权值。
(2)查询点x到点y的路径上结点权值之和。
(3)修改点x子树上各点的权值。
(4)查询点x子树上所有结点的权值之和。
其中的(1)是“树上差分”问题,见前一节的“倍增+差分”的解法。树上差分只能解决简单的修改问题,对(3)这样的修改整棵子树问题,树上差分就行不通了。
1、重链的DFS序
前面给出的函数dfs2(),是先DFS重儿子,再DFS轻儿子。如果在dfs2()的第一句用编号id[x]记录结点x的DFS序:
id[x] = ++num;
对每个结点重新编号的结果,例如下图:
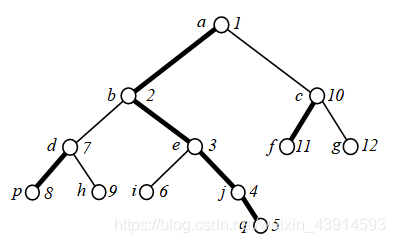
容易观察到:
(1)每一条重链内部结点的编号是有序的。重链{a, b, e, j, q}的DFS序是{1, 2, 3, 4, 5};重链{d, p}的DFS序是{7, 8};重链{c, f}的DFS序是{10, 11}。
(2)每棵子树上的所有结点的DFS序也是连续的。例如以e为根的子树{e, i, j, q},它们的DFS序是{3, 4, 5, 6}。
下面是关键内容:用线段树处理重链。由于每条重链内部的结点是有序的,可以按DFS序,把它们安排在一个线段树上。把每条重链看成一个连续的区间,对一条重链内部的修改和查询,用线段树来处理;若x到y的路径跨越了多个重链,简单地跳过即可。
概况地说:“重链内部用线段树,重链之间跳过”。
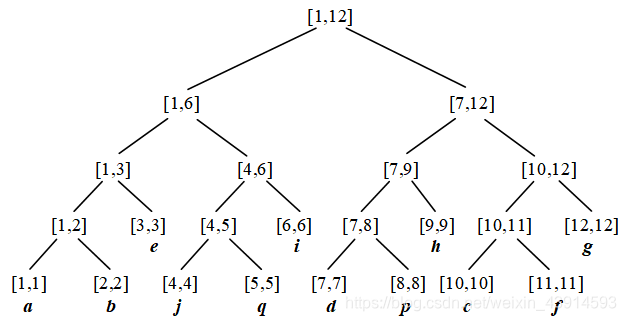
上图把树链的结点重新安排在一个线段树上。同一个重链的结点,在线段树上是连续的。
2、修改从结点x到y的最短路径上结点权值
x、y的最短路径经过LCA(x, y),这实际上是一个查找LCA(x, y)的过程。借助重链来修改路径上的结点的权值:
(1)令x的链头的深度更深,即top[x] ≥ top[y]。从x开始往上走,先沿着x所在的重链往上走,修改这一段的结点;
(2)到达x的链头后,跳过1个轻边,到达上一个重链;
(3)继续执行(1)、(2),直到x和y位于同一条重链上,再修改此时两个点之间的结点权值。结束。
例如修改从p到q的路径上所有结点权值之和:
(1)从p走到它的链头top[p] = d,修改p和d的权值;
(2)跳到b;
(3)b和q在同一条重链上,修改从b到q的权值;结束。
用线段树处理上述过程,仍以修改从p到q的路径上结点之和为例:
(1)从p跳到链头d,p和d属于同一条重链,用线段树修改对应的[7, 8]区间;
(2)从d穿过轻边(b, d),到达b所在的重链;
(3)查b到q,它们属于同一个重链,用线段树修改对应区间[2, 5],结束。
3、查询从x到y的路径上所有结点权值之和
查询与修改的过程几乎是一样的,以查询从p到q的路径上结点之和为例:
(1)从p跳到链头d,p和d属于同一条重链,用线段树查询对应的[7, 8]区间;
(2)从d穿过轻边(b, d),到达b所在的重链;
(3)查b到q,它们属于同一个重链,用线段树查询对应区间[2, 5],结束。
4、修改结点x的子树上各点的权值、查询结点x的子树上结点权值之和
每棵子树上的所有结点的DFS序是连续的,也就是说,每棵子树对应了一个连续的区间。那么修改和查询子树,和线段树对区间的修改和查询操作完全一样。
下面用一个模板题给出代码。
轻重链剖分 洛谷 P3384
题目描述:已知一棵包含n个结点的树(连通且无环),每个结点上包含一个数值,有以下4种操作:
1 x y z 修改:将树从x到y结点最短路径上所有结点的值都加上z。
2 x y 查询:求树从x到 y 结点最短路径上所有结点的值之和。
3 x z 修改:将以x为根节点的子树内所有结点值都加上z。
4 x 查询:求以x为根节点的子树内所有结点值之和。
输入格式:
第一行包含4个正整数n、m、r、p,分别表示树的结点个数、操作个数、根结点点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含n个非负整数,分别依次表示各个结点上初始的数值。
接下来n−1行每行包含两个整数x,y,表示点x和点y之间连有一条边(保证无环且连通)。
接下来m行每行包含若干个正整数,每行表示一个操作。
输出格式:输出包含若干行,分别依次表示每个操作2或操作4所得的结果(对P取模)。
数据规模:1≤n≤105,1≤m≤105,1≤r≤N,1≤p≤231-1
首先用链式前向星存树,然后用dfs1()、dfs2()剖链。这部分内容和前一小节“树链剖分求LCA”的内容几乎一样。唯一不同的地方在dfs2()中,加了id[x],对结点重新编号,这些编号是重链的DFS序,准备用线段树处理它们。
接下来是线段树。建线段树build()、打lazy标记addtag()、上传标记push_up()、下传标记push_down()、更新线段树update()、查询线段树query(),这些代码直接套用了第4章的“线段树”这一节的模板,内容几乎一样,只是把线段树内的结点看成重链的DFS序。
最后是本题的4个操作:
(1)update_range(),操作1,把从x到y的最短路径上的所有结点值加z。与求LCA(x, y)的过程差不多:让x和y沿着各自的重链往上跳,直到最后x和y处于同一个重链上。当x或者y在重链内部时,把这条重链看成线段树的一个区间,用线段树的update()处理;在重链之间的轻边上,简单地穿过轻边即可。
(2)query_range(),操作2,查询从x到 y 结点最短路径上所有结点的值之和。与操作1的步骤差不多,不同的地方是用线段树的查询函数query()。
(3)update_tree(),操作3,把以x为根节点的子树内所有结点值都加上z。就是线段树的update()。
(4)query_tree(),操作4,查询以x为根节点的子树内所有结点值之和。就是线段树的query()。
下面给出代码,基本上是“链式前向星+线段树+树剖”的简单组合,编码虽然有点长,但是不难。
#include<bits/stdc++.h>
using namespace std;
const int maxn=100000+10;
int n,m,r,mod;
//以下是链式前向星
struct Edge{int to, next;}edge[2*maxn];
int head[2*maxn], cnt;
void init(); //与前一小节“洛谷P3379树链剖分”的init()一样
void addedge(int u,int v); //与前一小节“洛谷P3379树链剖分”的addedge()一样
//以下是线段树
int ls(int x){ return x<<1; } //定位左儿子:x*2
int rs(int x){ return x<<1|1;} //定位右儿子:x*2 + 1
int w[maxn],w_new[maxn]; //w[]、w_new[]初始点权
int tree[maxn<<2], tag[maxn<<2]; //线段树数组、lazy-tag操作
void addtag(int p,int pl,int pr,int d){ //给结点p打tag标记,并更新tree
tag[p] += d; //打上tag标记
tree[p] += d*(pr-pl+1); tree[p] %= mod; //计算新的tree
}
void push_up(int p){ //从下往上传递区间值
tree[p] = tree[ls(p)] + tree[rs(p)]; tree[p] %= mod;
}
void push_down(int p,int pl, int pr){
if(tag[p]){
int mid = (pl+pr)>>1;
addtag(ls(p),pl,mid,tag[p]); //把tag标记传给左子树
addtag(rs(p),mid+1,pr,tag[p]); //把tag标记传给右子树
tag[p] = 0;
}
}
void build(int p,int pl,int pr){ //建线段树
tag[p] = 0;
if(pl==pr){
tree[p] = w_new[pl]; tree[p] %= mod;
return;
}
int mid = (pl+pr) >> 1;
build(ls(p),pl,mid);
build(rs(p),mid+1,pr);
push_up(p);
}
void update(int L,int R,int p,int pl,int pr,int d){
if(L<=pl && pr<=R){
addtag(p, pl, pr,d);
return;
}
push_down(p,pl,pr);
int mid = (pl+pr) >> 1;
if(L<=mid) update(L,R,ls(p),pl,mid,d);
if(R> mid) update(L,R,rs(p),mid+1,pr,d);
push_up(p);
}
int query(int L,int R,int p,int pl,int pr){
if(pl>=L && R >= pr)
return tree[p] %= mod;
push_down(p,pl,pr);
int res =0;
int mid = (pl+pr) >> 1;
if(L<=mid) res += query(L,R,ls(p),pl,mid);
if(R> mid) res += query(L,R,rs(p),mid+1,pr);
return res;
}
//以下是树链剖分
int son[maxn],id[maxn],fa[maxn],deep[maxn],siz[maxn],top[maxn];
void dfs1(int x, int father); //与前一小节“洛谷P3379树链剖分”dfs1()一样
int num = 0;
void dfs2(int x,int topx){ //x当前节点,topx当前链的最顶端的节点
id[x] = ++num; //对每个结点新编号
w_new[num] = w[x]; //把每个点的初始值赋给新编号
top[x]=topx; //记录x的链头
if(!son[x]) return; //x是叶子,没有儿子,返回
dfs2(son[x],topx); //先dfs重儿子
for(int i=head[x];~i;i=edge[i].next){ //再dfs轻儿子
int y=edge[i].to;
if(y!=fa[x] && y!=son[x])
dfs2(y,y); //每一个轻儿子都有一条从它自己开始的链
}
}
void update_range(int x,int y,int z){ //和求LCA(x, y)的过程差不多
while(top[x]!=top[y]){
if(deep[top[x]]<deep[top[y]])
swap(x,y);
update(id[top[x]],id[x],1,1,n,z); //修改一条重链的内部
x = fa[top[x]];
}
if(deep[x]>deep[y]) swap(x,y);
update(id[x],id[y],1,1,n,z); //修改一条重链的内部
}
int query_range(int x,int y){ //和求LCA(x,y)的过程差不多
int ans=0;
while(top[x]!=top[y]){ //持续往上跳,直到若x和y属于同一条重链
if(deep[top[x]]<deep[top[y]])
swap(x,y); //让x是链头更深的重链
ans += query(id[top[x]],id[x],1,1,n); //加上x到x的链头这一段区间
ans %= mod;
x = fa[top[x]]; //x穿过轻边,跳到上一条重链
}
if(deep[x]>deep[y]) //若LCA(x, y) = y,交换x, y
swap(x,y); //让x更浅,使得id[x] <= id[y]
ans += query(id[x],id[y],1,1,n); //再加上x, y的区间和
return ans % mod;
}
void update_tree(int x,int k){ update(id[x],id[x]+siz[x]-1,1,1,n,k); }
int query_tree(int x){ return query(id[x],id[x]+siz[x]-1,1,1,n) % mod; }
int main(){
init(); //链式前向星初始化
scanf("%d%d%d%d",&n,&m,&r,&mod);
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
for(int i=1;i<n;i++){
int u,v; scanf("%d%d",&u,&v);
addedge(u,v); addedge(v,u);
}
dfs1(r,0);
dfs2(r,r);
build(1,1,n); //建线段树
while(m--){
int k,x,y,z; scanf("%d",&k);
switch(k){
case 1: scanf("%d%d%d",&x,&y,&z);update_range(x,y,z); break;
case 2: scanf("%d%d",&x,&y); printf("%d
",query_range(x,y));break;
case 3: scanf("%d%d",&x,&y); update_tree(x,y); break;
case 4: scanf("%d",&x); printf("%d
",query_tree(x)); break;
}
}
}
5、把边权转为点权
上面的例题处理的是结点权值问题,有的树是边权问题,例如:一棵树有n个结点,由n-1条边连接,给出边的权值,做两种操作,(1)查询两个结点之间的路径长度;(2)修改第i条路径的权值。
如果把边权转为点权,就能按前面给出的“树链剖分 + 线段树”来解决。
例如下图(1),若把边权转为点权,显然只能把每条边上的边权赋给这条边下层的结点,得到图(2)。编程操作是:比较边(u, v)的两点的deep[u]、deep[v],把边权赋给更深的那个结点。

转换为点权后,树剖的操作基本上一样。但是,区间求和和区间更新操作都有一点问题。
(1)区间求和。例如图(1)求从d到e的路径,d-b-e的长度是7 + 3 = 10;但是图(2)变成了7 + 2 + 3 = 12,多算了b点的权值。
(2)区间修改。例如图(1)中把从d到e的路径上的边d-b、b-e都减1,此时边b-a并没有被影响到;但是在图(2)中,把d、b、e三个结点的值都减了1,而b点的值是不该被减的。
观察到b = LCA(d, e),所以解决方法是不要处理LCA:
(1)区间[L, R]求和时,不计算LCA(L, R)的值;
(2)区间[L, R]更新时,不更新LCA(L, R)的值。
【树链剖分习题】
洛谷:P2486、P2146、P2590、P3178、P3038
Hdu: 3966、4897、5029、6547
Poj: 2763、3237