什么是算法
算法是用于解决特定问题的一系列的执行步骤,使用不同算法,解决同一个问题,效率可能相差非常大
比如:求第 n 个斐波那契数(fibonacci number)
/** * 斐波那契数列 Fibonacci sequence * 斐波那契数列(Fibonacci sequence),又称黄金分割数列、 * 因数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”, * 指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、…… * 在数学上,斐波那契数列以如下被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*) */ public static int fibonacciSequence_01(int i){ if(i<=1){ return i; } return fibonacciSequence_01(i-1)+fibonacciSequence_01(i-2); } public static int fibonacciSequence_02(int n){ if(n<=1){ return n; } int first=0; int second=1; for (int i=0;i<n-1;i++){ int sum=first+second; first=second; second=sum; } return second; }
如何评判一个算法的好坏?
如果单从执行效率上进行评估,可能会想到这么一种方案 : 比较不同算法对同一组输入的执行处理时间 .这种方案也叫做:事后统计法
此方案有比较明显的缺点 1.执行时间严重依赖硬件以及运行时各种不确定的环境因素 2.必须编写相应的测算代码 3.测试数据的选择比较难保证公正性
还可以从以下维度来评估算法的优劣
- 正确性、可读性、健壮性(对不合理输入的反应能力和处理能力)
- 时间复杂度(time complexity):估算程序指令的执行次数(执行时间)
- 空间复杂度(space complexity):估算所需占用的存储空间
大O表示法(Big O)
一般用大O表示法来描述复杂度,它表示的是数据规模 n 对应的复杂度,此方法忽略常数、系数、和低阶
◼ 注意:大O表示法仅仅是一种粗略的分析模型,是一种估算,能帮助我们短时间内了解一个算法的执行效率
对数阶的细节
log2n = log29 ∗ log9n
所以 log2n 、log9n 统称为 logn
常见的复杂度
下图来自维基百科

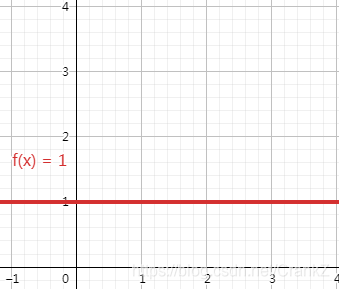
常数级别O(1)
O(1):算法复杂度和问题规模无关。换句话说,哪怕你拿出几个PB的数据,我也能一步到位找到答案。
理论上哈希表就是O(1)。因为哈希表是通过哈希函数来映射的,所以拿到一个关键字,用哈希函数转换一下,就可以直接从表中取出对应的值。和现存数据有多少毫无关系,故而每次执行该操作只需要恒定的时间
(当然,实际操作中存在冲突和冲突解决的机制,不能保证每次取值的时间是完全一样的)
对数级别O(logN)
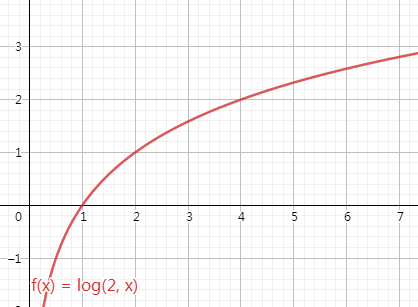
O(logN):算法复杂度和问题规模是对数关系。换句话说,数据量大幅增加时,消耗时间/空间只有少量增加(比如,当数据量从2增加到2^64时,消耗时间/空间只增加64倍,常见于二分法
int number = 1; // 语句执行一次 while (number < n) { // 语句执行logn次 // 这里的2是log的底数 // 底数在大O符号中是省去的 number *= 2; // 语句执行logn次 }
线性级别O(N)
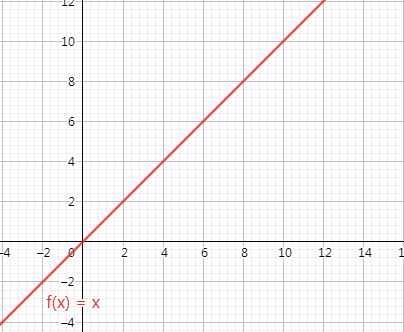
O(n):算法复杂度和问题规模是线性关系。换句话说,随着样本数量的增加,复杂度也随之线性增加
int i =0; // 语句执行一次 while (i < n) { // 语句执行n次 print(i); //语句执行n次 i++; // 语句执行n次 }
线性对数级别O(NlogN)

public static void test6(int n) { // log5(n) // O(logn) while ((n = n / 5) > 0) { System.out.println("test"); } }
平方级别O(N^2)
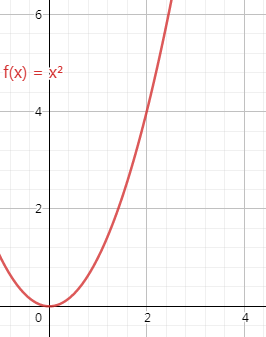
O(n^2)计算的复杂度随着样本个数的平方数增长。这个例子在算法里面,就是那一群比较挫的排序,比如冒泡等等
for (int i = 0; i < n; i++) { // 语句执行n次 for (int j = 0; j < n; j++) { // 语句执行n^2次 print('I am here!'); // 语句执行n^2 } }
指数级别O(2^N)
如果一个算法的运行时间是指数级的(exponential),一般它很难在实践中使用
斐波那契数的例子的第一个算法就是O(2^N)
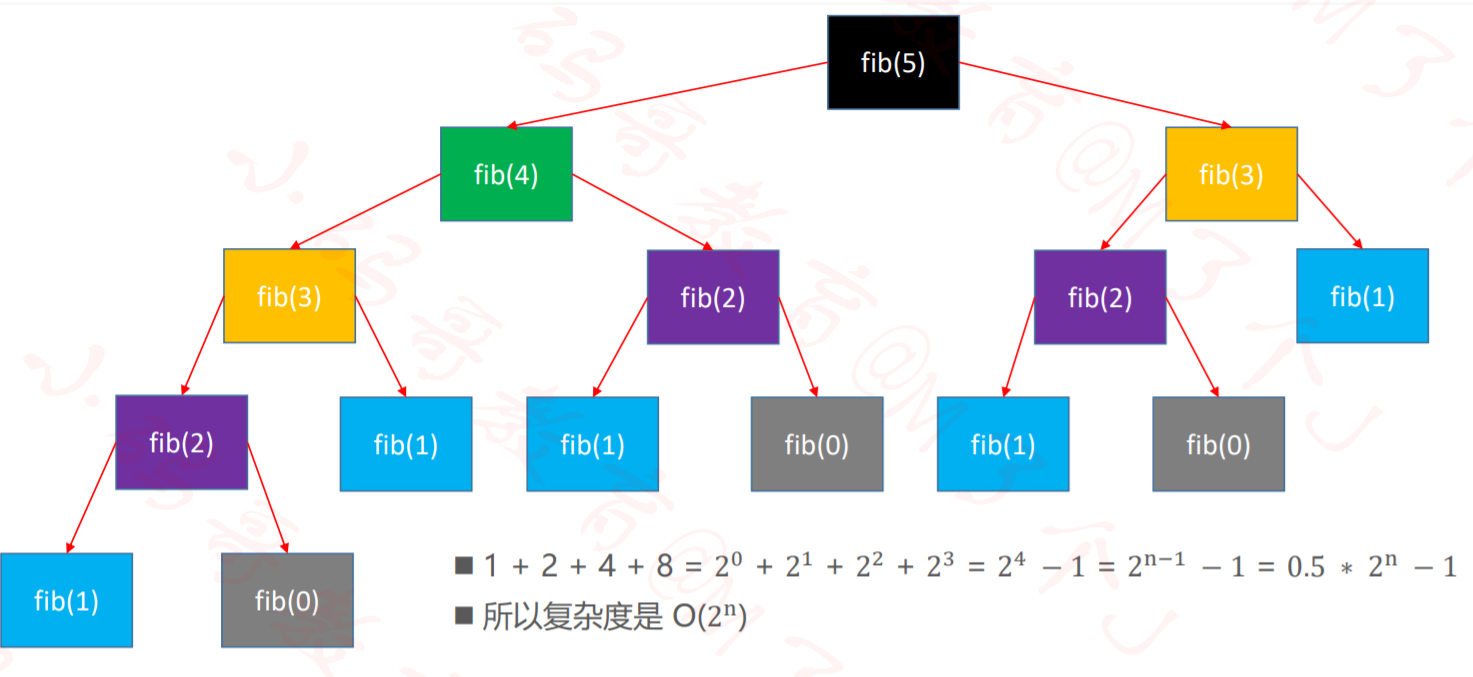
有时候算法之间的差距,往往比硬件方面的差距还要大
算法的优化方向
1.用尽量少的存储空间
2.用尽量少的执行步骤(执行时间)
3.根据情况,可以
- 空间换时间
- 时间换空间