2020牛客寒假算法基础集训营1

F maki和tree

 

思路：

用到并查集的思想

如图：

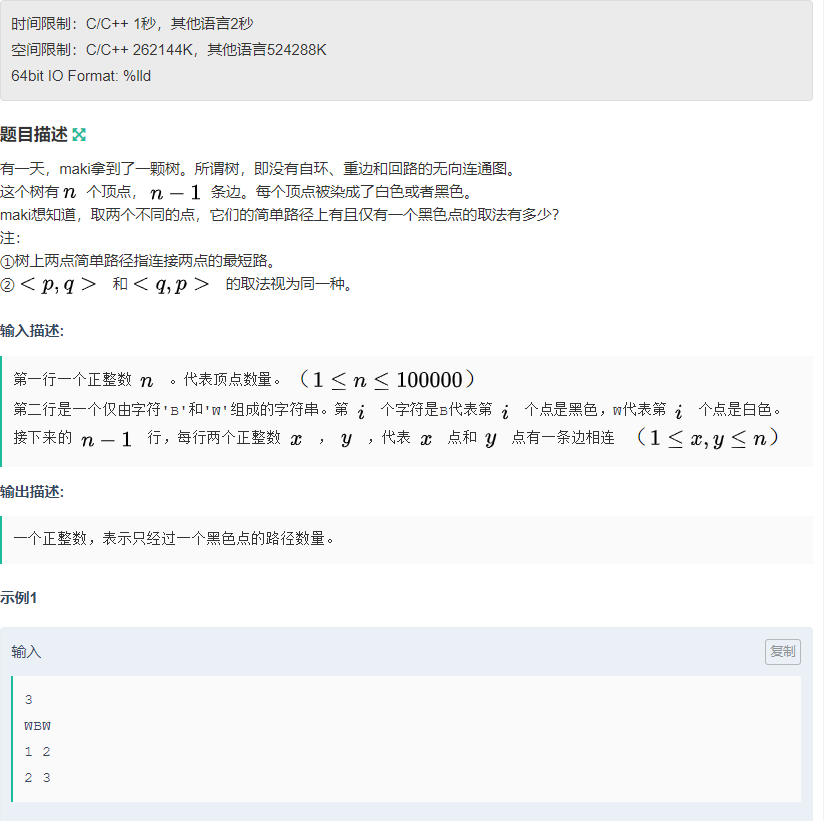
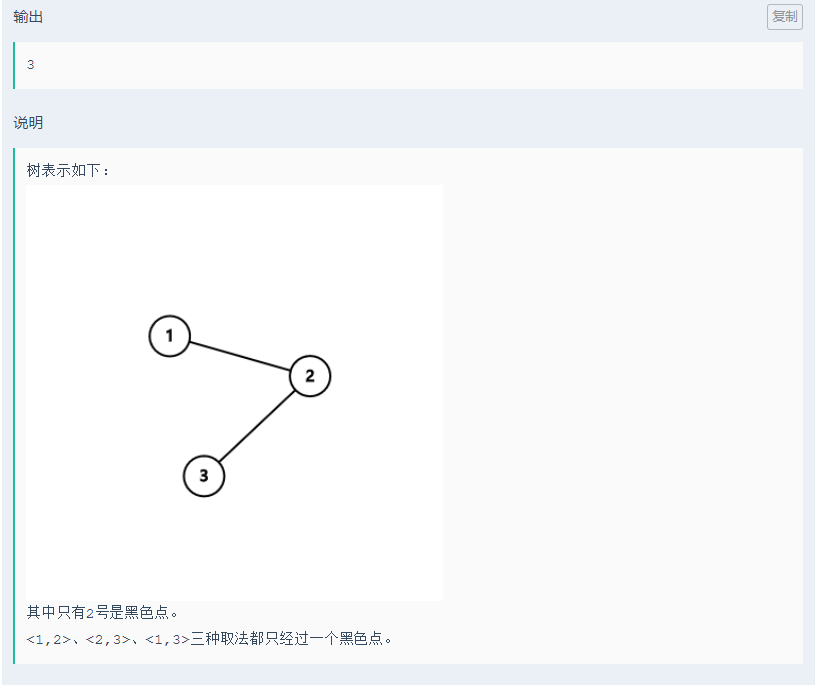
简单路径上只有一个黑色点的方案：第一种端点有一个为黑色点，第二种两端点均为白色点，端点连接的线路中有一个黑色点

ans = (1+2+3)+1*2+2*3+1*3 = （1+2+3）+1*（2+3）+2*3

 代码：

#include<iostream>
#include<stdio.h>
#include<vector>
using namespace std;
typedef long long ll;
const int maxn = 1e5+10;
vector<int>e[maxn];
int f[maxn],size[maxn];
char s[maxn];

int find(int x){
    if(f[x]==x)
        return x;
     return f[x] = find(f[x]);
    
}
void merge(int x,int y){
    int t1 = find(x);
    int t2 = find(y);
    if(t1!=t2){
        f[t2] = t1;
        size[t1]+=size[t2];
    }
}
int main(){
    int n;
    cin>>n;
    cin>>s+1;
    for(int i=1;i<=n;i++){
        if(s[i]=='W')
            size[i]++;
        f[i]=i;
    }
    for(int i=1;i<=n-1;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        e[x].push_back(y);
        e[y].push_back(x);
        if(s[x]==s[y]&&s[x]=='W'){
            merge(x,y);
        }
    }
    ll ans = 0;
    for(int i=1;i<=n;i++){
        if(s[i]=='B'){
            ll sum=0;
            for(auto v:e[i]){
                sum+=size[find(v)];
            }
            ans+=sum;
            for(auto v:e[i]){
                sum-=size[find(v)];
                ans+=sum*size[find(v)];
            } 
        }
    }
    cout<<ans<<endl;
    return 0;
}

J u's的影响

思路：

f(1) = x;

f(2）= y;

f(3)=x*y*(a^b);

f(4)=x*(y^2)*(a^b)^2;

f(5) = (x^2)*(y^3)*(a^b)^4;

f(6) = (x^3)*(y^5)*(a^b)^7;

f:                f(1)    f(2)   f(3)   f(4)   f(5)   f(6)   f(7)    f(8）

x的系数  ：  1       0       1      1      2       3       5     8

y的系数 ：   0       1       1      2      3       5      8     13

a^b的系数：0       0       1      2      4       7      12    20

红色数字：斐波拉契数列 

a^b的系数 = x的系数+y的系数-1

这道题用到了费马小定理：例子 （3^100)%13 = (3^(12*8+4))%13 = (3^4)%13

   p为质数 a,b均为非负 (a^b)%p   = (a%p)^(b%(p-1))%p

 代码：

#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
struct mat{
    ll a[2][2];
};
 
mat mat_mul(mat x,mat y){
    mat res;
    memset(res.a,0,sizeof(res.a));
    for(ll i=0;i<2;i++){
        for(ll j=0;j<2;j++){
            for(ll k=0;k<2;k++){
                res.a[i][j] = (res.a[i][j]+(x.a[i][k]*y.a[k][j])%(mod-1))%(mod-1);
            }
        }
    }
    return res;
}
 
mat quM(mat t,ll b){
    mat ans;
    memset(ans.a,0,sizeof(ans.a));
    ans.a[0][0]=1;
    ans.a[1][1]=1;
    while(b){
        if(b&1) ans = mat_mul(t,ans);
        t = mat_mul(t,t);
        b>>=1;
    }
    return ans;
}
  
ll qui(ll a,ll b){
    a=a%mod;
    ll t = 1;
    while(b){
        if(b&1) t = t*a%mod;
        a = a*a%mod;
        b>>=1;
    }
    return t;
}
int main(){
    ll n,x,y,a,b;
    cin>>n>>x>>y>>a>>b;
    mat ans;
    ans.a[0][0]=1;
    ans.a[0][1]=1;
    ans.a[1][0]=1;
    ans.a[1][1]=0;
    ll cx=0,cy=0,c=0;
    if(n==1){
        cx=1;cy=0;c=0;
    }
    else{
        ans = quM(ans,n-1);
      　cx = ans.a[1][1]%(mod-1)+mod-1;
      　cy = ans.a[1][0]%(mod-1)+mod-1;
        c = cx+cy-1;//避免c为mod 貌似是这样
    }
    cout<<((qui(x,cx)%mod*qui(y,cy))%mod*qui(qui(a,b),c%(mod-1)))%mod<<endl;
    return 0;
}