min cost max flow算法示例

问题描述

给定g个group，n个id，n<=g.我们将为每个group分配一个id(各个group的id不同)。但是每个group分配id需要付出不同的代价cost，需要求解最优的id分配方案，使得整体cost之和最小。

例子

例如以下4个group，三个id，value矩阵A：

value	id1	id2	id3
H1	4	3	0
H2	1	0	0
H3	2	0	2
H4	3	1	0

id_i分配给H_j的代价(changing cost[i, j]=sum(A[j,:])-A[j,i])。
例如，如果给H1指定id1，则value=4被保留，但是需要付出changing cost为3.

我们需要为H1-H4分别指定一个id1-id3,id4(新建的id)，目标是是的总体的changing cost最小。
例子中最优的分配结果是：
H1 <- id2,
H2 <- New ID,
H3 <- id3,
H4 <- id1,
对应的changing cost=8 (4 + 1 + 2 + 1)。

Min-cost Max flow算法

Use min-cost max flow here
Connect source to all ids with capacity 1, connect each id to each h with capacity 1 and cost= -a[id[i], h[j]] (as you need to find maximums actually), and then connect all hs with sink with capacity 1.
After applying min-cost max flow, you will have flow in those (i, j) where you should assign i-th id to j-th h. New ids for other hs.

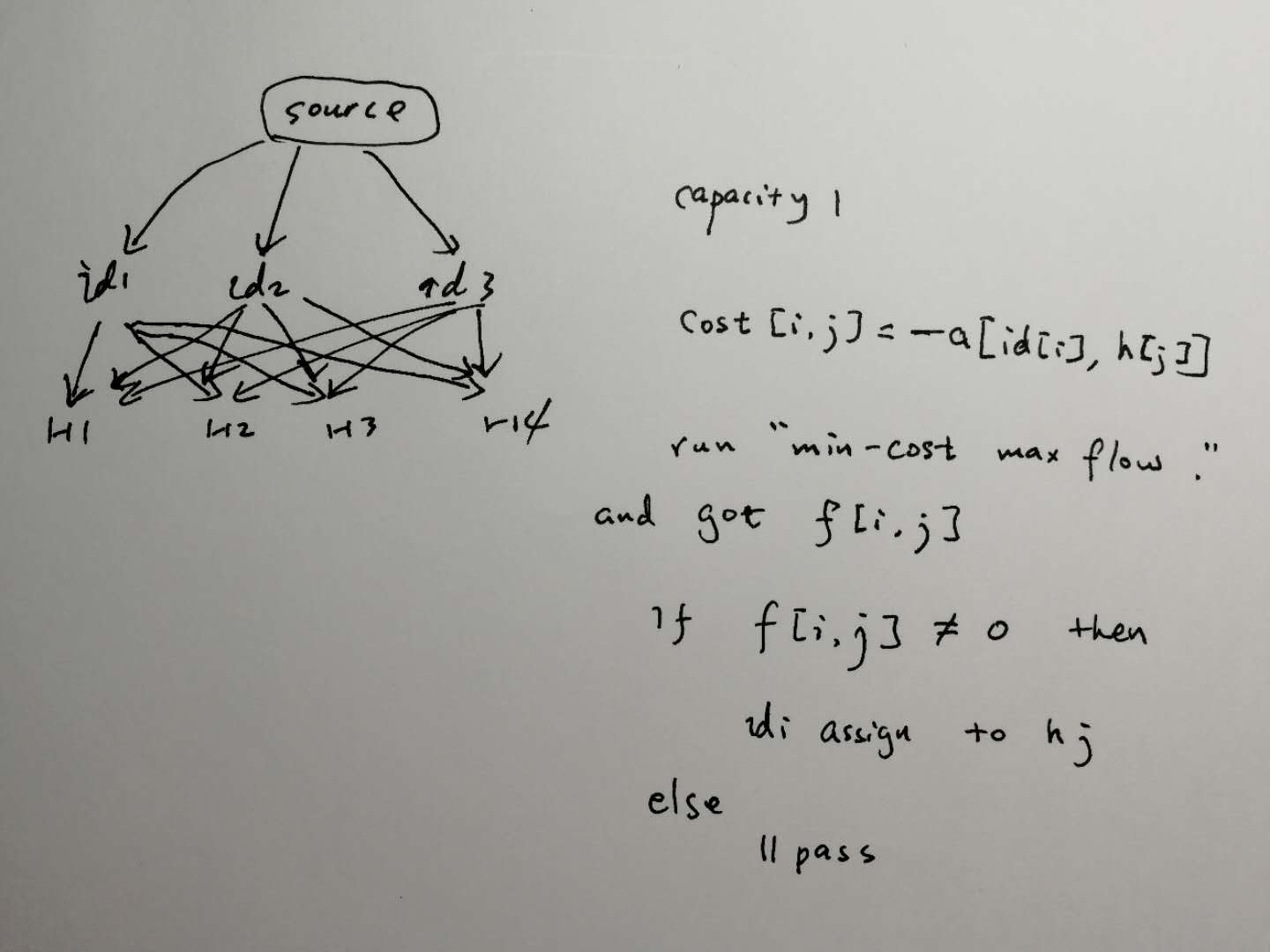
因为capacity=1，算法最终结果f[i,j]只可能取值0/1。所以，如果f[i,j]=1，则id_i被分配给h_j.

---

Here is a possible solution of the problem with some help of [min cost max flow algorithm:
http://web.mit.edu/~ecprice/acm/acm08/MinCostMaxFlow.java https://en.wikipedia.org/wiki/Minimum-cost_flow_problem.

The basic idea is to translate consumer id, group id to vertex of graph, translate our constrains to constrains of MinCostMaxFlow problem.

As for POC, I used the source code from website (web.mit.edu), did some change and checked in the algorithm to trunk.
I added unit test RuleBasedOptimizerTest.test6() to test the 66x 4 case, which runs successfully in milliseconds.
Also, test was done on the data which caused time out before, and this time it is fast.

Steps of the algorithm:

Create the flow network:

1. Introduce a source vertex, a sink vertex;
2. Each consumerid is a vertex, each groupid is a vertex;
3. Connect source to each consumerId, each edge has capacity 1;
4. Connect each consumerId to groupId, each edge has capacity 1;
5. Connect each groupId to sink, each edge has capacity 1;
6. The cost of a(u, v) is from the cost table, but we need to take -1 x frequency.

Calculate max flow of the network, and get the flow matrix.

• If there is flow from cid_i to gid_k then we assign the cid_i to the gid_k;
• If there is no flow to gid_k, then we assign a new id to gid_k.

Algorithm complex

is O(min(|V|^2 * totflow, |V|^3 * totcost)), where |V|=(#groupid + #consumerId + 2).