Voting classifier
多种分类器分别训练,然后分别对输入(新数据)预测/分类,各个分类器的结果视为投票,投出最终结果:
训练:
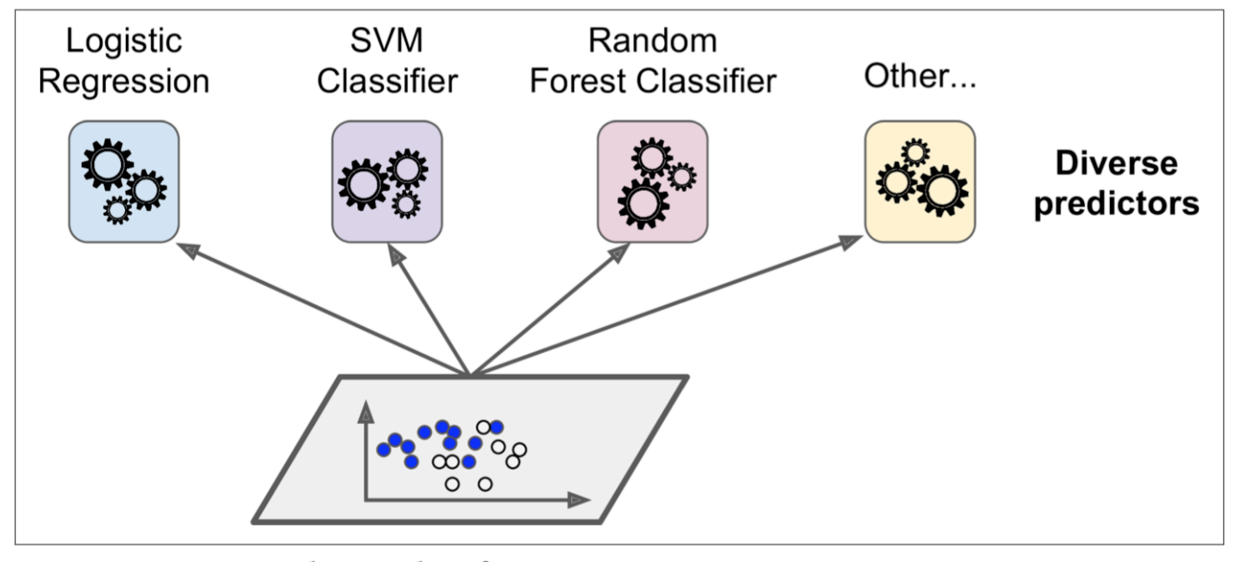
投票:

为什么三个臭皮匠顶一个诸葛亮。通过大数定律直观地解释:
一个硬币P(H)=0.51。大数定律保证抛硬币很多次之后,平均得到的正面频数接近(0.51 imes N),并且N越大,越接近。那么换个角度,N表示同时掷硬币的人数,即为这边的N个臭皮匠,他们的结果合到一起就得到的是接近真实结果的值。
进一步根据中心极限定理,即二项分布以正态分布为其极限分布定律,可以计算“N次抛硬币后,header占大多数的概率”
例如P(H)=0.51,N=1000,则(Pr( ext{Header 占大多数}) = 1-Phi (frac{n/2 - np}{sqrt{np(1-p)}})=Phi(0.63)=0.74),当N=10000,(Pr=Phi(2)=0.98)
Bagging and Pasting
跟投票的思路不同,Bagging(boost aggregating)的思路是同一算法训练多个模型,每个模型训练时只使用部分数据。预测时,每个模型分别给出自己的预测结果,再将这些结果聚合起来。
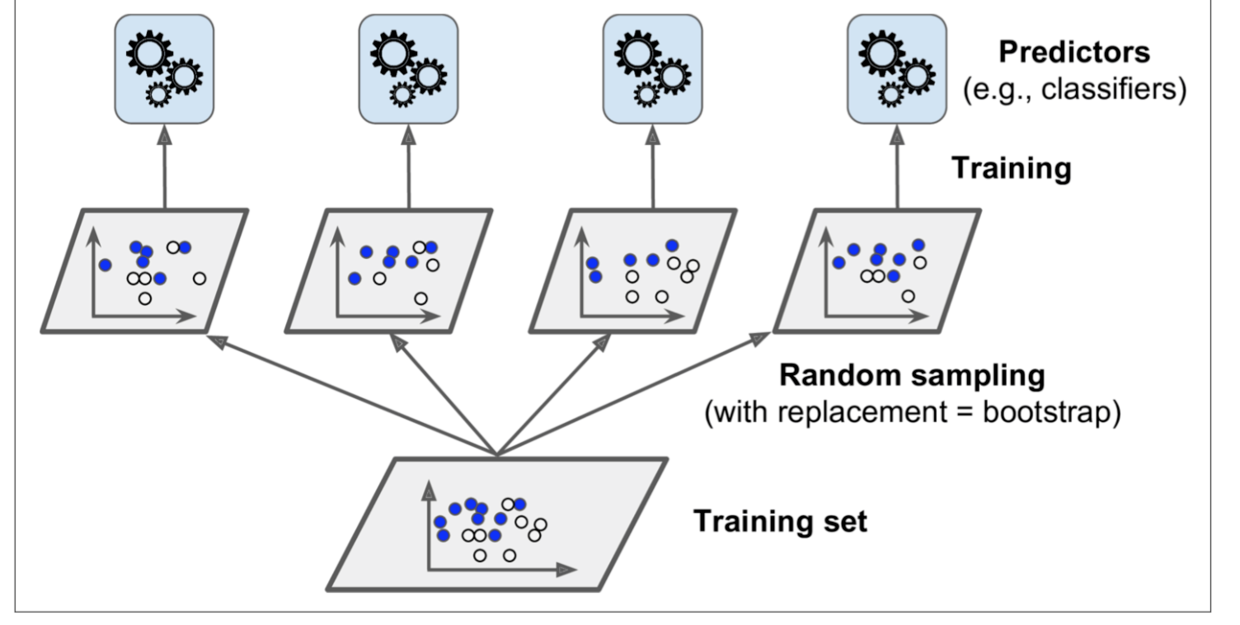
Out Of Bag
因为每个模型训练时随机选择每个训练sample数据,那么,对于某个sample而言,有可能被选中0次或多次。如果一个sample没有被选中,那么它很自然地可以被用做交叉验证。
某个sample至少被一个模型训练用到的概率,(Pr( ext{sample被选中})=1-left( 1- frac{1}{N}
ight)^k)
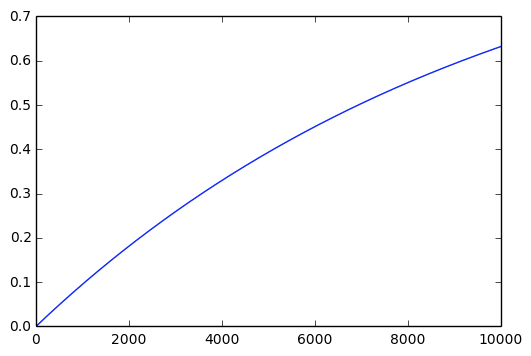
(k=N), (lim_{N oinfty}1-left(1-frac{1}{N} ight)^N=1-e^{-1} =0.63)
parallel training pattern
bagging算法需要训练多个模型,每个模型的训练过程相同,只是算法使用的数据不同。联想到并行训练的问题,两种思路:
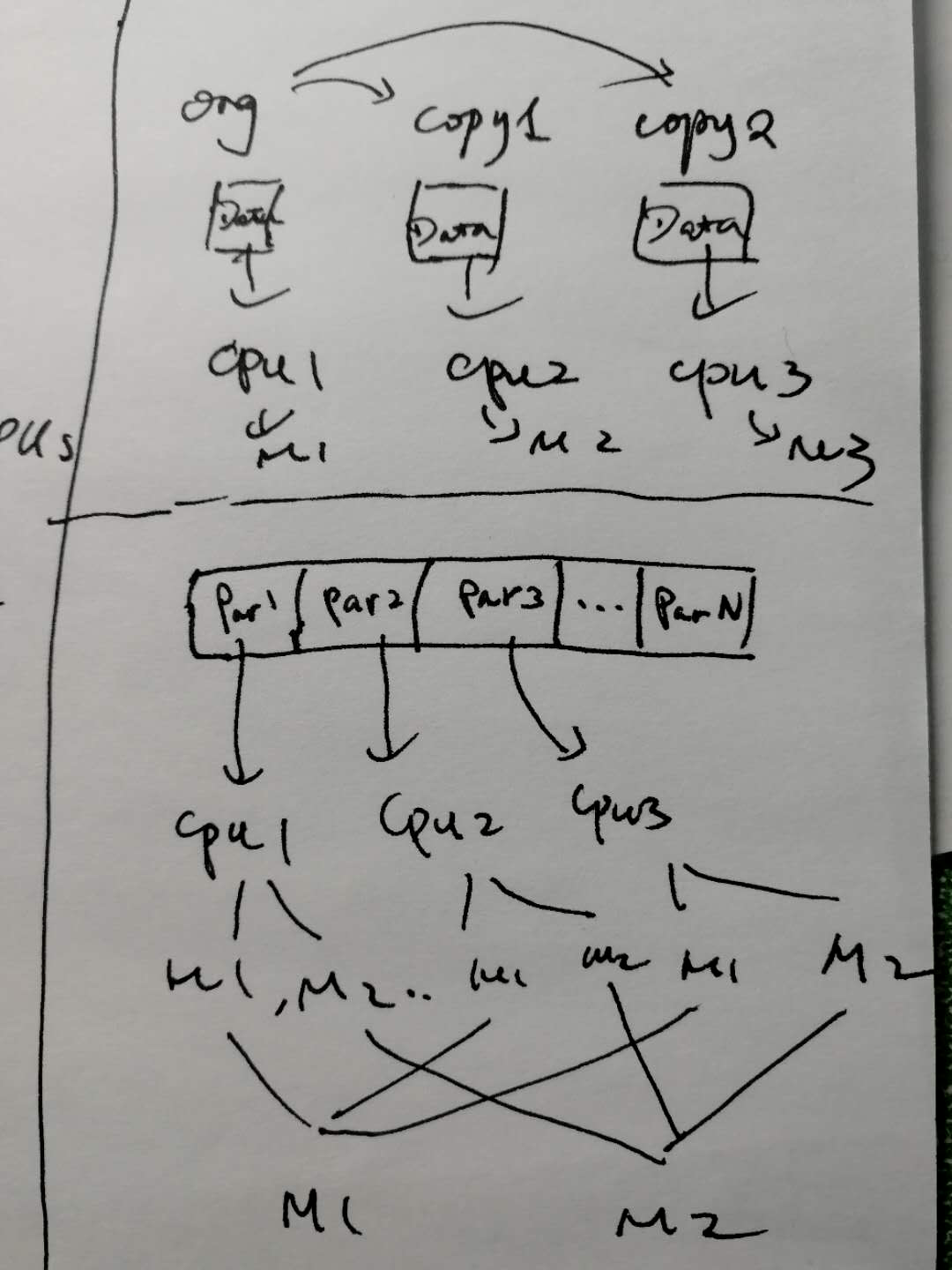
- 如果训练样本数比较小,每个模型能够承受所有数据,那么使用上面的模式。
- 如果训练样本很大,需要分区到多个cpu/节点上,那么每个节点只消费部分训练样本,但是每个节点可以同时训练多个模型,最终再把各个模型的半成品结合到一起形成完整的模型。
随机森林
随机森林一般采用bagging算法训练模型。
rnd_clf = RandomForestClassifier(n_estimators=500, max_leaf_nodes=16, n_jobs=-1)
bag_clf = BaggingClassifier(
DecisionTreeClassifier(splitter="random", max_leaf_nodes=16),
n_estimators=500, max_samples=1.0, bootstrap=True, n_jobs=-1
)
Feature Importance
Lastly, if you look at a single Decision Tree, important features are likely to appear closer to the root of the tree, while unimportant features will often appear closer to the leaves (or not at all). It is therefore possible to get an estimate of a feature’s importance by computing the average depth at which it appears across all trees in the forest.
Boosting
定义:any Ensemble method that can combine several weak learners into a strong learner. The general idea of most boosting methods is to train predictors sequentially, each trying to correct its predecessor.
AdaBoosting
如果各一个样本被predecessor分类器误分类了,那么下一个分类器将会更重视这个样本(boost/提升这个样本)。
所以在顺序训练模型时,每个样本的重要性在变化:

Gradient Boosting
Gradient Boosting也是通过不断增加predictor来修正之前的predictor。不同于adaboost的地方是,gradient boosting调整每个样本的权重,后面的predictor直接去拟合前面的predictor的残差(residual error).
Stacking (stacked generalisation)
多层训练模型的雏形。