如何判断一个点是否在多边形内部?
(1)面积和判别法:判断目标点与多边形的每条边组成的三角形面积和是否等于该多边形,相等则在多边形内部。
(2)夹角和判别法:判断目标点与所有边的夹角和是否为360度,为360度则在多边形内部。
(3)引射线法:从目标点出发引一条射线,看这条射线和多边形所有边的交点数目。如果有奇数个交点,则说明在内部,如果有偶数个交点,则说明在外部。
具体做法:将测试点的Y坐标与多边形的每一个点进行比较,会得到一个测试点所在的行与多边形边的交点的列表。在下图的这个例子中有8条边与测试点所在的行相交,而有6条边没有相交。如果测试点的两边点的个数都是奇数个则该测试点在多边形内,否则在多边形外。在这个例子中测试点的左边有5个交点,右边有三个交点,它们都是奇数,所以点在多边形内。
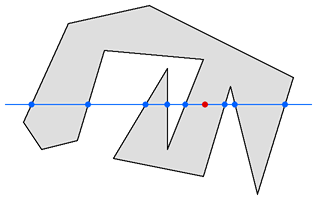
算法图解:

关于这个算法的具体的更多图形例子:http://alienryderflex.com/polygon/
参考代码:
int pnpoly(int nvert, float *vertx, float *verty, float testx, float testy) { int i, j, c = 0; for (i = 0, j = nvert-1; i < nvert; j = i++) { if ( ((verty[i]>testy) != (verty[j]>testy)) && (testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) ) c = !c; } return c; }
来自一个polygon的内部实现:
public bool IsInside(PointLatLng p) { int count = Points.Count; if(count < 3) { return false; } bool result = false; for(int i = 0, j = count - 1; i < count; i++) { var p1 = Points[i]; var p2 = Points[j]; if(p1.Lat < p.Lat && p2.Lat >= p.Lat || p2.Lat < p.Lat && p1.Lat >= p.Lat) { if(p1.Lng + (p.Lat - p1.Lat) / (p2.Lat - p1.Lat) * (p2.Lng - p1.Lng) < p.Lng) { result = !result; } } j = i; } return result; }
特殊情况:要检测的点在多变形的一条边上,射线法判断的结果是不确定的,需要特殊处理(If the test point is on the border of the polygon, this algorithm will deliver unpredictable results)。
计算一个多边形的面积(area of a polygon):
private static double SignedPolygonArea(List<PointLatLng> points) { // Add the first point to the end. int pointsCount = points.Count; PointLatLng[] pts = new PointLatLng[pointsCount + 1]; points.CopyTo(pts, 0); pts[pointsCount] = points[0]; for (int i = 0; i < pointsCount + 1; ++i) { pts[i].Lat = pts[i].Lat * (System.Math.PI * 6378137 / 180); pts[i].Lng = pts[i].Lng * (System.Math.PI * 6378137 / 180); } // Get the areas. double area = 0; for (int i = 0; i < pointsCount; i++) { area += (pts[i + 1].Lat - pts[i].Lat) * (pts[i + 1].Lng + pts[i].Lng) / 2; } // Return the result. return area; } /// <summary> /// Get the area of a polygon /// </summary> /// <param name="points"></param> /// <returns></returns> public static double GetPolygonArea(List<PointLatLng> points) { // Return the absolute value of the signed area. // The signed area is negative if the polygon is oriented clockwise. return Math.Abs(SignedPolygonArea(points)); }
参考资料:
http://alienryderflex.com/polygon/
http://en.wikipedia.org/wiki/Point_in_polygon
http://www.codeproject.com/Tips/84226/Is-a-Point-inside-a-Polygon