写在前面
本文学习内容来自《算法图解》一书及百度百科内容
算法是一组完成任务的指令。任何代码片段都可视为算法。 —— 摘自《算法图解》1
快速排序
以下内容摘自百度百科
快速排序(Quicksort)是对冒泡排序的一种改进。
快速排序由C. A. R. Hoare在1962年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
实现思路
分而治之(divide and conquer, D&C)一种著名的递归式问题解决方法。
这里有个问题,请读者思考一下
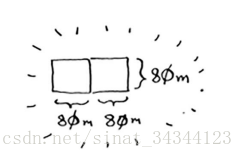
假如你是一个农场主,现在你有一块土地,想要给它均匀的分成大小相同的方块。
如果要你来均匀的分开成一个个小方块你会怎么做? 像下面这样?
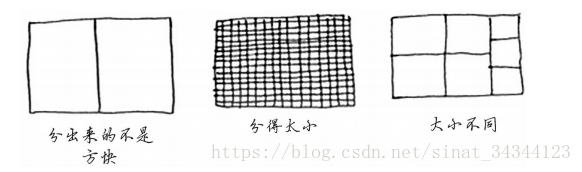
显然这是愚蠢的,也是不可能的。那我们应该怎么样去做呢?
这里就用到了我们上面提到的D&C策略 ,D&C策略是使用递归的,解决这个分成两个步骤:
- 找到基准条件,这个条件,必须尽可能的简单。
- 竟可能的缩短范围找到基准,将给定条件不断缩小范围。
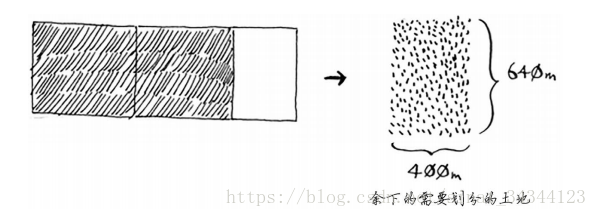
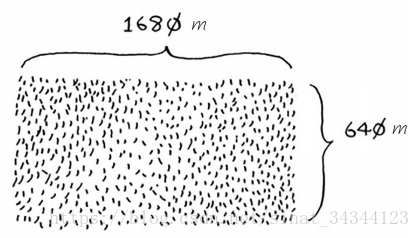
1、我们先按照给定的宽度 640m 将长切成 ( 640m + 640m + 400m ) × 640m 大小的三块方块
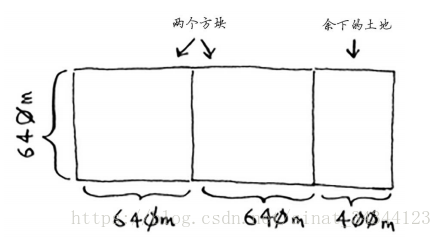
这样我们就得到了一个 400m × 640m 的小方块
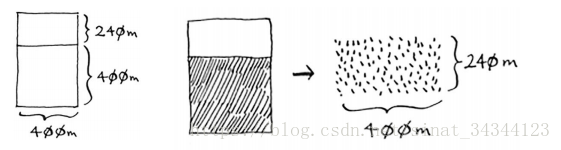
2、再按照 400m × 400m 分成 2 块
640 m × 400 m的土地,可从中划出的最大方块为400 m × 400 m。 这样就会余下一个 400m × 240m 的一个方块。
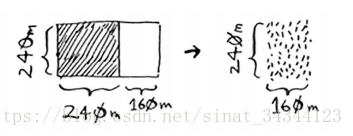
3、我们在把余出的 400m × 240m 切成 240m × 240m + 240m × 160m
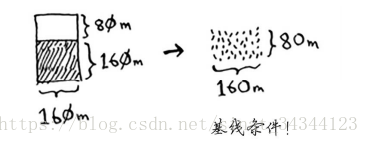
4、以此类推
最终我们找到了想要的小方块 80m × 80m 这样我们就把最初的 1680m × 640m 分成了 1680 个 80m × 80m 的小方块
以上讲述的只是一种解决问题的思路,也是D&C策略的具体体现,那我们现在回顾一下解决问题的过程。
- 我们拿到问题之后,是想要找到问题的基准条件。
- 紧接着我们把适应问题条件的范围不断的缩小。
- 在更小的范围去寻找我们想要的答案。
其实我们在解决这个问题的时候,已经用到了一个算法,那就是《欧几里德算法》,具体大家可以查看百度百科即可
实际例子
说了这么多,那如果是实际的问题我们该如何解决呢?
- 快速排序说的是怎么去给一个数组,或者列表进行一个有序的排列。
// 如果我们有这样一个数组
int[] ints = {1};
// 那我们说,这是不需要排序的,直接返回结果就可以
[1]// 如果是有两个值呢
int[] ints = {1, 2};
// 这个也很简单,只需要比较两个数值的大小即可
[1, 2]// 如果是有三个值呢
int[] ints = {1, 2, 0};
[?, ?, ?]
// 如果是有多个值呢
int[] ints = {1, 23, 12, 34, 87, 45, 68, 15};
[?, ?, ?, ?, ?, ?, ?, ?]同样我们使用的也是D&C策略来解决这个问题,首先要找到一个基准条件。那我们说这个条件怎么去找?
先别急,我们来看最后一个数组
int[] ints = {1, 23, 12, 34, 87, 45, 68, 15};首先我们要做的事情很简单,找到一个基准条件,缩小我们的排序范围。无论多少个值,我们只进行两个值得比较。
int temp = ints[0]那我们说,temp 就是我们要的小范围的一个基准条件,所有的数字和这个基准条件去比较。那就变成了两个值得比较。
ints [1] = 23; // 大于temp
ints [2] = 12; // 大于temp
ints [3] = 34; // 大于temp
...
...比较的之后的值怎么办 ,我们把比较的值分成两组,要么大于基准值,要么小于等于基准值。大于的,我们放到基准值的右侧,小于等于的,我们放到基准值的左侧。并且,如果出现位置转换的时候,我们的基准值得位置是在跟着变动的。我们比较的顺序是从数组的第一个和数组最后一个进行比较。依次像中间靠拢。
/*
* 我们如果拿数组的第一个数字进行比较,那数组将会被分成两个部分
* 要么大于1,要么小于等于1
* 结果数组会变成这个样子
* [1, 23, 12, 34, 87, 45, 68, 15]
* /看过之后你可能会有疑虑,这什么啊?怎么没有变化呢?是的,因为我们选取的基准值1,大于它的放到右侧,因为其它的数字全部大于1,所以我们放到了右侧。接下来再看。
现在我们可以理解为,原来数组被拆成了两个数组
由原来的[1, 23, 12, 34, 87, 45, 68, 15]
变成了现在的[]和[23, 12, 34, 87, 45, 68, 15]
其实看似没有变化,实则我们已经缩小了排序的范围,再一次我们需要对两个数组进行之前的方法进行计算
数组 [23, 12, 34, 87, 45, 68, 15]进行我们接下来的选取基准值,进行比较分开大小。因为我们的基准值选取的是23,所以 12 15 在 23 的左侧,其余的在 23 右侧,那具体的结果是什么样子的呢?
同样的我们的数组被
[23]分隔成了两部分
分成了[15, 12][87, 45, 68, 34]
快速排序实现原理
可能有的同学看到这里会有疑问,为什么 15 在 12 的左侧,这就是上面我们提到的比较之后改变数字位置的问题,我们开始比较的时候是 23 和 15 去比较,显然 15 比 23 小,所以它要放到 23 的左侧,那此时的 23 将会和 15 的位置互换,这样就达到了小的数字在基准值的左侧,当我们在拿基准值 23 和 左侧的数字比较的时候,23 比 12 大,保持不变,依次 23 比 34 小,此时由要进行位置互调。23 出现在了 34 的位置上,34 则在了 23 的位置上。重点来了,基准条件在做完一次基准值之后,不会再次参与后续排序。
此时我们又要对拆分出的数组进行比较
[15, 12]用同样的基准值办法进行比较显然变成了[12, 15]
而[87, 45, 68, 34]则变成了[34, 45, 68, 87]
以此类推,我们的数组对应的变化如下:
[1, 23, 12, 34, 87, 45, 68, 15]
[1, 15, 12, 23, 87, 45, 68, 34]
[1, 12, 15, 23, 87, 45, 68, 34]
[1, 12, 15, 23, 34, 45, 68, 87]
[1, 12, 15, 23, 34, 45, 68, 87]
[1, 12, 15, 23, 34, 45, 68, 87]相信看到现在,多多少少大家已经掌握了快速排序法的原理。
- 找到一个基准值
- 将其与数字与该基准值进行比较
- 比较成功后按大小,改变数字位置,基准值被隔离开来,用来连接数组。(这里比较抽象,需要一定的自行脑补)
- 对重新组成的数组再次进行 1 2 3 步骤
为了大家学习和调试方便,下面提供了快速排序的 java 和 python 的代码
Java
public static void main(String args[]) {
int[] ints = {1, 23, 12, 34, 87, 45, 68, 15};
quickSort(ints, 0, ints.length - 1);
}
private static void quickSort(int[] ints, int low, int high) {
int h = high;
int l = low;
if (l < h) {
int temp = ints[l];
while (l < h) {
while (l < h && ints[h] > temp) {
h--;
}
ints[l] = ints[h];
while (l < h && ints[l] <= temp) {
l++;
}
ints[h] = ints[l];
}
ints[l] = temp;
System.out.println(Arrays.toString(ints));
quickSort(ints, low, h - 1);
quickSort(ints, l+ 1, high);
}
}[1, 23, 12, 34, 87, 45, 68, 15]
[1, 15, 12, 23, 87, 45, 68, 34]
[1, 12, 15, 23, 87, 45, 68, 34]
[1, 12, 15, 23, 34, 45, 68, 87]
[1, 12, 15, 23, 34, 45, 68, 87]
[1, 12, 15, 23, 34, 45, 68, 87]python
def quickSort(array):
if len(array) < 2:
return array
else:
pivot = array[0]
less = [i for i in array[1:] if i <= pivot]
greater = [i for i in array[1:] if i > pivot]
return quickSort(less) + [pivot] + quickSort(greater)
print(quickSort([1, 23, 12, 34, 87, 45, 68, 15]))