2 出色的物理引擎
卡罗拉最近沉迷于ark游戏,游戏中的地图上有n个浮空的石头围成了一圈,在优秀的物理引擎支持下,这些石头会自动落下。她发现石头落下的顺序是有规律的。一共有n个石头,从第一块石头开始数,数到第m个石头,那块就是第一个落下的石头;之后从第一个落下的石头后一个重新从1开始数,同样数到第m个石头,那个就是第二个落下的石头;以此类推。为了方便,对这些石头从1开始编号。卡罗拉现在想知道最后落下的是那一块石头?
输入格式
输入包含两个整数n和m (1<=m,n<=1000)。
输出格式
输出一 个整数,代表最后落下的石头的编号。
输入样例
10 3
输出样例
4
Accepted
这一题一开始我想用链表的方法解决,因为在链表中,我们删去其中一个石子的操作会显得很便捷,那么具体方法可以见下方的链接。
最后也是我觉得这题我应该学到的东西,那就是使用约瑟夫环解决问题。但是说真的,在理解的时候还是费了好一番功夫。这里截取了一些,上述原文的分析过程。不得不说这是一篇宝藏文章,分析的很透彻。老规矩还是先上代码:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int main()
{
int n;
int m;
int i;
int ans=0;
cin >> n >> m;
for(i=1;i<=n;i++){
ans=(ans+m)%i;//约瑟夫环
}
cout << ans+1;//注意这里的输出
return 0;
}
真的,比上面两种方法所需要写的代码量少了超级多,直接一个公式就解决了问题。
下面开始进行分析:
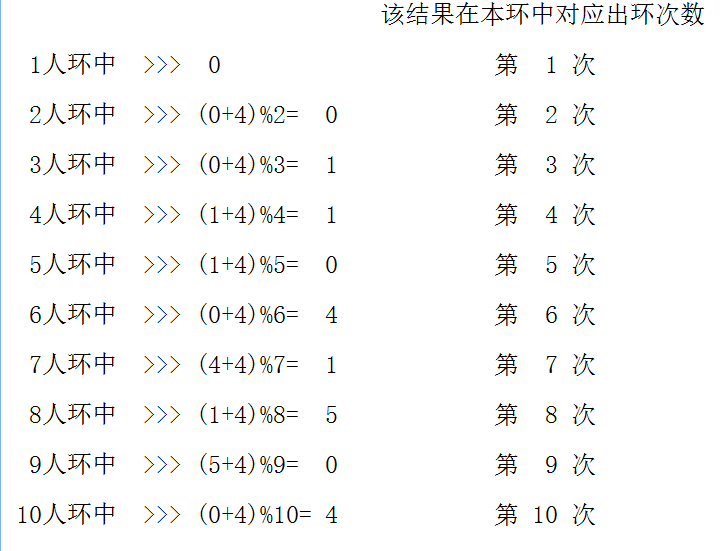
例如有十个石子,编号0~9(为什么?理由是由于m是可能大于n的,而当m大于等于n时,那么第一个出列的人编号是m%n,而m%n是可能等于0的,这样编号的话能够简化后续出列的过程)
注意 以下图示中的环数字排列都是顺序的,且从编号0开始。
由图知,10人环中最后入海的是4号,现由其在1人环中的对应编号0来求解。
3 开机方案
h学长有个机器用来完成任务。现在有n个任务,第i个任务(1<= i <= n)在ti时刻开始,并在ti + 1时刻结束。同一时刻不会有多个任务。 h学长可以在任何时刻开启机器,不过每一次开启机器都会消耗1点能量。h学长只有k点能量可以用于开启机器。但是机器开着的时候需要消耗燃料,显然让机器一直开着并不一定是最好的选择。现在h学长想利用自己具备的k点能量,有效的控制机器的开启,使得机器完成n个任务消耗的燃料尽可能的少。那么对应给出的n个任务以及h学长拥有的能量数,你能帮帮他吗? 提示:消耗的燃料要尽可能的少,即机器工作的时间尽可能的短。
输入格式
第一行包括两个整数 n和k(1<= n <= 1e5, 1<= k <=n) ,表示有 n个任务和h学长拥有k点能量。
接下来 n行,每行一个整数ti(1<= ti <=1e9),表示第 i 个任务在ti 时刻开始,并在ti + 1时刻结束 。
输出格式
输出一行包含一个整数,表示机器工作的最少时间。
输入样例1
3 2
1
3
6
输出样例1
4
样例1说明:
h学长有2点能量,可以用于两次机器的开启。 h学长会在时刻1 即第一个任务开始时开启机器,并在第二个任务结束时关闭机器; h学长会在时刻6 即第三个任务开始时开启机器,并在第三个任务结束时关闭机器。 机器总工作时间为 (4-1)+(7-6)=4 。
输入样例2
10 5
1
2
5
6
8
11
13
15
16
20
输出样例2
12
样例2说明: h学长有5点能量,可以用于5次机器的开启。 h学长会在时刻1 即第1个任务开始时开启机器,并在第2个任务结束时刻3关闭机器; h学长会在时刻5 即第3个任务开始时开启机器,并在第4个任务结束时刻7关闭机器; h学长会在时刻8 即第5个任务开始时开启机器,并在第5个任务结束时刻9关闭机器; h学长会在时刻11 即第6个任务开始时开启机器,并在第9个任务结束时刻17关闭机器; h学长会在时刻20 即第10个任务开始时开启机器,并在第10个任务结束时刻21关闭机器; 机器总工作时间为 (3-1)+(7-5)+(9-8)+(17-11)+(21-20)=12 。 开机、关机时刻不唯一。
Accepted
做到这题的时候,我其实想到了我们第一次上机练习的兼容任务那一题,那么那一题的思想是我把结束时间根据大小从小到大进行排序,然后在一定的时间内完成多个任务。那我这题也使用类似的思想,假设现在我从第一个任务开始的时间打开机器(k--),并且保持开机状态直到最后一个任务结束,算出总共需要的时间。然后在k仍然还大于0的情况下,我根据前后任务时间间隔大小由大到小排序,然后在k还有剩余的情况下,依次扣除这些间隔,这样答案就得到了。这题的思想主要是逆序扣除的思想,因为如果从头开始算的话,并不是特别好算,但是我现在倒一头来算的话,反而是问题简单化。代码如下:
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <string.h>
using namespace std;
struct machine{
int begin;
int end;
int diff;
}t[1000005];
bool cmp1(machine a,machine b){
return a.begin <b.begin;
}
bool cmp2(machine a,machine b){
return a.diff > b.diff;
}
int main(){
int n;
int k;
int i=1;
int ans=0;
cin >> n >> k;
for(i=1;i<=n;i++){
cin >> t[i].begin;
t[i].end=t[i].begin+1;
}
sort(t+1,t+1+n,cmp1);
ans=t[n].end-t[1].begin;
k--;
for(i=1;i<n;i++){
t[i].diff=t[i+1].begin-t[i].end;
}
t[n].diff=0;
sort(t+1,t+1+n,cmp2);
for(i=1;i<=n&&k!=0;i++){
ans-=t[i].diff;
k--;
}
cout << ans;
return 0;
}
4 特殊的翻译
小明的工作是对一串英语字符进行特殊的翻译:当出现连续且相同的小写字母时,须替换成该字母的大写形式,在大写字母的后面紧跟该小写字母此次连续出现的个数;与此同时,把连续的小写字母串的左侧和右侧的字符串交换位置;重复该操作,直至没有出现连续相同的小写字母为止。现在小明想请你帮他完成这种特殊的翻译。
输入格式
输入一串由小写字母构成的字符串。(字符串长度不大于250)
输出格式
输出翻译后的字符串。
输入样例1
dilhhhhope
输出样例1
在这里给出相应的输出。例如:
opeH4dil
输入样例2
lodnkmgggggggoplerre
输出样例2
在这里给出相应的输出。例如:
eG7lodnkmR2ople
Accepted
对于这一题的处理,让我再一次感觉到
string在处理字符串的方便性。但是特别要注意的是,在处理字符串的时候,不要忽略连续字母个数可能超过10,这也是我一开始错的地方。
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <string.h>
using namespace std;
int main(){
string s;
char str[10];
cin >> s;
int i,j,k,t;
int flag=0;
int num=0,temp;//num出现次数
for(i=0;i<s.size();i++){
string s1;
t=0;
if(s[i]==s[i+1]&&s[i]>='a'&&s[i]<='z'){//出现连续相同的小写字母
num=1;
for(j=i+1;j<s.size();j++){
if(s[j]==s[i]) num++;
else break;
}
s[i]-=32;//小写->大写
if(num<10)s[i+1]=num+'0'; //如果num值小于10
else{//如果num值大于10
temp=num;
while(temp){
str[t]=temp%10+'0';
temp/=10;
t++;
}
}
for(;j<s.size();j++){
s1+=s[j];
// cout << j << endl;
}
s1+=s[i];
if(num<10)s1+=s[i+1];
else
for(t--;t>=0;t--)
s1+=str[t];
for(k=0;k<i;k++)
s1+=s[k];
s=s1;
flag=1; //发现字符串做了改变,所以从头开始重新扫
}
if(flag==1){
flag=0;
i=-1;
}
}
cout << s << endl;
return 0;
}
5 好吃的巧克力
超市正在特价售卖巧克力,正好被贪吃的Lucky_dog看见了。巧克力从左到右排成一排,一共有N个,M种。超市有一个很奇怪的规定,就是你在购买巧克力时必须提供两个数字a和b,代表你要购买第 a 个至第 b 个巧克力(包含 a 和 b)之间的所有巧克力。假设所有巧克力的单价均为1元。Lucky_dog想吃所有种类的巧克力,但又想省钱。作为Lucky_dog的朋友,他请你来帮他决定如何选择购买巧克力时的 a 和 b。
输入格式
第一行包含两个正整数 N 和 M(M<=N, N<=10^6 , M<=2000),分别代表巧克力的总数及种类数。
第二行包含 N 个整数,这些整数均在1 至 M 之间,代表对应的巧克力所属的种类。
输出格式
输出仅一行,包含两个整数a和 b(a<=b) ,由一个空格隔开,表示花费最少且包含所有种类巧克力的购买区间。
数据保证有解,如果存在多个符合条件的购买区间,输出a最小的那个。
输入样例
12 5
2 5 3 1 3 2 4 1 1 5 4 3
输出样例
在这里给出相应的输出。例如:
2 7
Accepted
这一题刚开始就觉得直接用暴力遍历去寻找最优解就可以了,但是后面会发现有的点运行超时了,所以很显然暴力求解法是行不通的。那么这里要引入一种方法尺取法
这里引用原文部分解释,来进行一个大概的介绍:
尺取法:顾名思义,像尺子一样取一段,借用挑战书上面的话说,尺取法通常是对数组保存一对下标,即所选取的区间的左右端点,然后根据实际情况不断地推进区间左右端点以得出答案。之所以需要掌握这个技巧,是因为尺取法比直接暴力枚举区间效率高很多,尤其是数据量大的时候,所以尺取法是一种高效的枚举区间的方法,一般用于求取有一定限制的区间个数或最短的区间等等。当然任何技巧都存在其不足的地方,有些情况下尺取法不可行,无法得出正确答案。
使用尺取法时应清楚以下四点:
1、 什么情况下能使用尺取法? 2、何时推进区间的端点? 3、如何推进区间的端点? 3、何时结束区间的枚举?
尺取法通常适用于选取区间有一定规律,或者说所选取的区间有一定的变化趋势的情况,通俗地说,在对所选取区间进行判断之后,我们可以明确如何进一步有方向地推进区间端点以求解满足条件的区间,如果已经判断了目前所选取的区间,但却无法确定所要求解的区间如何进一步得到根据其端点得到,那么尺取法便是不可行的。首先,明确题目所需要求解的量之后,区间左右端点一般从最整个数组的起点开始,之后判断区间是否符合条件在根据实际情况变化区间的端点求解答案。
很显然对于这一题来说,我们就是先找到包括m种巧克力的区间的右端点,然后有左端点逐步逼近右端点,答案就可以解出来了,注意在我们比较是否为最少的时候,我们需要引用到区间长度,此时是否加1或减1这些小细节会影响结果,所以一定要细心思考。
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <string.h>
using namespace std;
int ch[1000005]={0};
int q[10000005]={0};
int main(){
int n,m; //巧克力的总数,种类数
int i,l=1,r=0;
int num=0;
cin >> n >> m;
for(i=1;i<=n;i++) cin >> ch[i];
int a,b,len=n;
while(l<=n&&r<=n){
while(num<m){
r++;
q[ch[r]]++;
if(q[ch[r]]==1) num++;
} //r值固定不变,接下来找出l的位置
if(num<m) break;
if(len>r-l+1&&num==m){
len=r-l+1;
a=l;
b=r;
}
q[ch[l]]--;
if(q[ch[l]]==0) {num--;}
l++;
}
cout << a <<" "<< b <<endl;
return 0;
}
6 下次一定(续)
你是一个bilibili的六级号,由于经常一键三连,所以一个硬币都没有,现在你又做了个梦,在梦中你制定了一个硬币增加规则:
第一天登陆后硬币总数1个,第二天登陆后硬币总数112个,第三天登陆硬币总数112123个......,以此类推,梦中不知日月,你瞬间拥有了11212312341234512345612345671234567812345678912345678910123456789101112345678910......无穷多个硬币。
常年维护B站秩序的百漂怪看不下去了,决定随机挑一个数x,作为这个无穷数的第x位,如果你能正确答对这第x位上的数是什么,就赠送给你与这个数等量的硬币。
百漂怪总共会挑t次。
你决定编程模拟一下,搏一搏,单车变摩托。
输入格式
第一行包含一个正整数t(1≤t≤10),表示百漂怪挑了t次。 接下来t行,每行一个正整数x (1 ≤ x≤ 2^31-1),表示第i次,百漂怪挑的是第x位。
输出格式
输出共t行,每行输出对应第x位上的数。
输入样例1
2
3
8
输出样例1
2
2
输入样例2
6
222
66666
99999999
66656565
22222
2
输出样例2
6
4
9
4
1
1
Accepted
我做这一题的主要思路是,将硬币数变化的规则分为i组,然后我们要找到x的位置对应的组数,然后根据这组所对应的字符串,寻找x对应的字符。
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <string.h>
using namespace std;
long long digi[100000]={0};//digi存位数
int main(){
int i,t,j=1;
long long sum=0;
char ans;
long long x;
int pos;
for(i=1;i<=32000;i++) //统计位数,由已知x≤2^31-1,可知最多可分31268组,即i的范围;
digi[i]=digi[i-1]+(int)(log10(i)+1);
cin >> t;
for(i=1;i<=t;i++){
cin >> x;
j=0;
sum=0;
while(1){
j++;
sum+=digi[j];
if(sum>=x) break;
}
string str;
for(int k=1;k<=j;k++){
char st[100000];
sprintf(st,"%d",k);
str+=st;
}
pos=(int)((digi[j]-1)-(sum-x));
ans=str[pos];
cout << ans << endl;
}
return 0;
}
7 小明选蛋糕
小明舍友生日快到了,他决定背着舍友偷偷为他准备一个蛋糕,但是蛋糕款式众多,他也很难选择,于是他决定根据蛋糕摆放的位置来缩小蛋糕选择的范围。
已知小明从第a个蛋糕开始选择,他规定一个比a大的数m(1<=a<m<=10^10),小明只对满足下式的x(0<=x<m)位置上的蛋糕感兴趣,gcd(a,m)=gcd(a+x,m)经过这样的筛选后,可供小明选择的蛋糕款式还剩多少呢?
输入格式
第一行包含一个整数T(1<=T<=50),表示输入数据共T组;
接下来共有T行,每行包含两个整数a和m (1<=a<m<=10^10)。
输出格式
输出共T行,每行一个整数k,表示经过筛选后可供小明选择的蛋糕款式的数量。
输入样例
3
4 9
5 10
42 9999999967
输出样例
6
1
9999999966
Wrong Answer
一开始我拿到题目,以为这一题非常简单,只不过就是写一个gcd函数就可以解决问题。但是当我提交代码的时候有四个点显示运行超时,然后我注意到题目m范围<=10^10,所以只能另外找一个方法,简化循环次数。
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <string.h>
using namespace std;
long long gcd(long long m,long long n)
{
if(m%n==0) return n;
else return gcd(n,m%n);
}
int main(){
long long m,a,j,b;
int i,t;
cin >> t;
for(i=1;i<=t;i++){
cin >> a >> m;
long long num=0;
b=gcd(a,m);
for(j=0;j<m;j++){
if(b==gcd(a+j,m))num++;
}
cout << num << endl;
}
return 0;
}
Accepted
既然模拟这条路走不通,那么显然,我们需要把角度放在另一种思路,我们注意到这一题很特别的条件就是
gcd(a,m)=gcd(a+x,m),那么我们如何利用这个关系来解决问题呢?通过搜索资料,我们了解到在解决求最大公约数的方法中,有一种简单且快捷的方法,那就是使用欧拉函数。这里简要介绍一下欧拉函数。(思路来源:yjs)
欧拉函数:就是对于一个正整数n,小于n且和n互质的正整数(包括1)的个数,记作(varphi(n))。
欧拉函数的通式:(varphi(n)=n(1-frac{1}{p_1})(1- frac{1}{p_2} )(1-frac{1}{p_3})(1-frac{1}{p_4})cdots(1-frac{1}{p_n})=ndisplaystyle prod^{n}_{i=1}(1-frac{1}{p_i}))
但我们注意到欧拉函数的使用要求是a和m互质,但是在本题中a与m不一定存在互质关系,因此需要我们进行进一步的转化,将a与m转化为互质数。也就是当我们用gcd函数求出这两个数之间的最大公约数n后,就可以得出(gcd(frac{a}{n},frac{m}{n})=gcd(frac{a+x}{n},frac{m}{n})=1)那么,现在(frac{a+x}{n},frac{m}{n})互质。但是,我们需要注意的是(frac{a+x}{n})的值有可能大于(frac{m}{n}),那么大于(frac{m}{n})的部分就不能使用欧拉函数求出了,并且小于(frac{a}{n})的部分会被记录。由gcd函数概念我们可以知道(gcd(frac{a+x}{n},frac{m}{n})=gcd((frac{a+x}{n})\%frac{m}{n},frac{m}{n})),可以知道超出的部分恰好由小于的部分所记录,因此我们只需求解(varphi(frac{m}{n})).
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <string.h>
using namespace std;
long long gcd(long long m,long long n)
{
if(m%n==0) return n;
else return gcd(n,m%n);
}
long long calculate(long long m){
long long ans=m;
for(long long i=2;i*i<=m;i++){
if(m%i==0){
ans=ans/i*(i-1);
while(m%i==0)m/=i;
}
}
if(m>1) ans=ans/m*(m-1); //因为数据范围为longlong,若先乘后除可能会导致数据溢出,故采用先除后乘
return ans;
}
int main(){
long long m,a,j,b;
int i,t;
cin >> t;
for(i=1;i<=t;i++){
cin >> a >> m;
long long num=0;
b=gcd(a,m);
/*for(j=0;j<m;j++){
if(b==gcd(a+j,m))num++;
}
num=calculate(m , a);*/
m/=b;
num=calculate(m);
cout << num << endl;
}
return 0;
}
8 走迷宫
你正在玩一个迷宫游戏,迷宫有n×n格,每一格有一个数字0或1,可以从某一格移动到相邻四格中的一格上。为了消磨时间,你改变了玩法,只许从0走到1或者从1走到0。
现在给你一个起点,请你计算从这个格子出发最多能移动多少个格子(包含自身)。
输入格式
第1行包含两个正整数n和m(1≤n≤1000,1≤m≤10000)。
接下来n行,对应迷宫中的n行,每行n个字符,字符为0或者1,字符之间没有空格。
接下来m行,表示m次询问。每行2个正整数i,j,表示从迷宫中第i行第j列的格子开始走。
输出格式
输出共m行,每行一个整数,分别对应于输入数据中的m次询问,给出最多能移动的格子数。
输入样例
2 2
01
10
1 1
2 2
输出样例
4
4
Accepted
(来源:洛谷)
这一题题目很好理解,但是做的时候确实一脸懵,不知道从何入手,这时候看到网上有一种叫DFS的做法也是第一次接触到这种算法,让我简略的码一下它的概念:
深度优先搜索算法(Depth First Search,简称DFS):一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件,搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为(O(n!))。
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <string.h>
using namespace std;
char a[1005][1005];
int ans[100005],pos[1005][1005],n,m,x,y;
void DFS(int x,int y,int z,int i){
if(x<0||x>=n||y<0||y>=n||pos[x][y]!=-1||a[x][y]-'0'!=z) return ;
pos[x][y]=i; //越界,已被搜索过,不满足01关系
ans[i]++;
DFS(x-1,y,!z,i);
DFS(x+1,y,!z,i);
DFS(x,y-1,!z,i);
DFS(x,y+1,!z,i);
}
int main(){
int i;
cin >> n >>m;
for(i=0;i<n;i++){
cin >> a[i];
}
memset(pos,-1,sizeof(pos));
for(i=0;i<m;i++){
cin>> x >> y;
x--;
y--;
if(pos[x][y]==-1){
DFS(x,y,a[x][y]-'0',i);
}
else ans[i]=ans[pos[x][y]];
}
for(i=0;i<m;i++){
cout << ans[i]<< endl;
}
return 0;
}