题意:棋盘上有n个棋子 每个棋子都有收益
现在给定1e5条线 有横着的 竖着的
规定只能在线的一侧选最多ki个棋子
问最大收益
题解:写自闭的一道题 很容易想到是网络流 但是建图有点难
第一道最大费用流 居然是边权取反 跑最小费用最大流!
先离散化坐标 然后可以用点代替一条横线 一条竖线
如果x,y有一个棋子 就将x所在的横线 向y所在的竖线连一个权值为1 收益为花费的边
这里要跑最大收益 所以收益要取反
同时从小到大的每相邻两个横线之间连一条收益为0 边权为x较小的点所受限制条件
竖线之间也连一条收益为0 边权为y较大的点所受限制条件
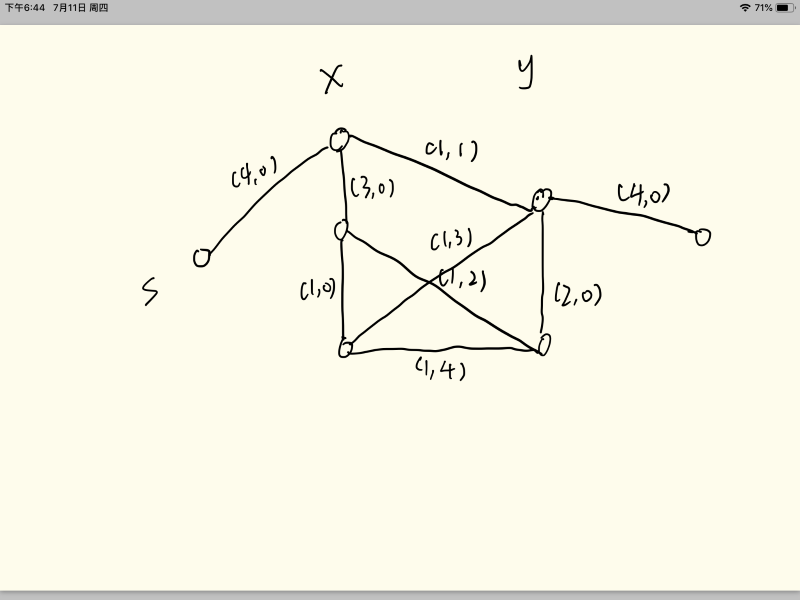
好像越扯越复杂了... 总之就是直接上图吧
左边表示x = 1, x = 2, x = 3三条线 右边表示y = 1, y = 2 两条线

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int INF = 0x3f3f3f3f; int n, m, s, t, cnt, maxflow; ll mincost; int cntx, cnty; int xid[505]; int yid[505]; int kx[505]; int ky[505]; struct po { int x, y, id; int tx, ty; }q[505]; bool cmp1(po A, po B) {return A.x < B.x;} bool cmp2(po A, po B) {return A.y < B.y;} bool cmp3(po A, po B) {return A.id < B.id;} int findx(int x) { if(x <= xid[1]) return 1; if(x > xid[cntx]) return -1; int l = 2, r = cntx; int mid = l + r >> 1; while(l + 1 < r) { mid = l + r >> 1; if(x >= xid[mid]) l = mid; else r = mid; } if(x <= xid[l]) return l; else return r; } int findy(int y) { if(y <= yid[1]) return 1; if(y > yid[cnty]) return -1; int l = 2, r = cnty; int mid = l + r >> 1; while(l + 1 < r) { mid = l + r >> 1; if(y >= yid[mid]) l = mid; else r = mid; } if(y <= yid[l]) return l; else return r; } struct node { int to, nex, val, cost; }E[100005]; int head[1005]; int cur[1005]; void addedge(int x, int y, int va, int cos) { E[++cnt].to = y; E[cnt].nex = head[x]; head[x] = cnt; E[cnt].val = va; E[cnt].cost = cos; E[++cnt].to = x; E[cnt].nex = head[y]; head[y] = cnt; E[cnt].val = 0; E[cnt].cost = -cos; } int inque[1005]; int dis[1005]; int vis[1005]; bool spfa() { for(int i = 1; i <= cntx + cnty + 2; i++) inque[i] = 0, dis[i] = INF, cur[i] = head[i]; queue<int> que; que.push(s); dis[s] = 0, inque[s] = 1; while(!que.empty()) { int u = que.front(); que.pop(); inque[u] = 0; for(int i = head[u]; i; i = E[i].nex) { int v = E[i].to; if(E[i].val > 0 && dis[v] > dis[u] + E[i].cost) { dis[v] = dis[u] + E[i].cost; if(!inque[v]) { inque[v] = 1; que.push(v); } } } } return dis[t] != INF; } int dfs(int x, int flow) { if(x == t) { vis[t] = 1; maxflow += flow; return flow; } vis[x] = 1; int used = 0; int rflow = 0; for(int i = cur[x]; i; i = E[i].nex) { cur[x] = i; int v = E[i].to; if(E[i].val > 0 && (!vis[v] || v == t) && dis[v] == dis[x] + E[i].cost) { if(rflow = dfs(v, min(flow - used, E[i].val))) { used += rflow; E[i].val -= rflow; E[i ^ 1].val += rflow; mincost += 1LL * E[i].cost * rflow; if(used == flow) break; } } } return used; } void dinic() { maxflow = mincost = 0; while(spfa()) { vis[t] = 1; while(vis[t]) { memset(vis, 0, sizeof(vis)); dfs(s, INF); } } } int main() { while(~scanf("%d", &n)) { cnt = 1; memset(kx, 0, sizeof(kx)); memset(ky, 0, sizeof(ky)); memset(head, 0, sizeof(head)); cntx = cnty = 0; for(int i = 1; i <= n; i++) scanf("%d%d", &q[i].x, &q[i].y), q[i].id = i; q[0].x = q[0].y = 0; sort(q + 1, q + 1 + n, cmp1); for(int i = 1; i <= n; i++) { if(q[i].x != q[i - 1].x) xid[++cntx] = q[i].x; q[i].tx = cntx; } sort(q + 1, q + 1 + n, cmp2); for(int i = 1; i <= n; i++) { if(q[i].y != q[i - 1].y) yid[++cnty] = q[i].y; q[i].ty = cnty; } sort(q + 1, q + 1 + n, cmp3); scanf("%d", &m); for(int i = 1; i <= m; i++) { getchar(); char a; int b, c; scanf("%c %d %d", &a, &b, &c); if(a == 'R') { int tmp = findx(b); if(tmp == -1) continue; if(kx[tmp] == 0) kx[tmp] = c; else kx[tmp] = min(kx[tmp], c); } else if(a == 'C') { int tmp = findy(b); if(tmp == -1) continue; if(ky[tmp] == 0) ky[tmp] = c; else ky[tmp] = min(ky[tmp], c); } } s = cntx + cnty + 1; t = s + 1; int lasx = n; for(int i = 1; i <= cntx; i++) { if(kx[i]) lasx = min(lasx, kx[i]); if(i == 1) addedge(s, i, lasx, 0); else addedge(i - 1, i, lasx, 0); } int lasy = n; for(int i = 1; i <= cnty; i++) { if(ky[i]) lasy = min(lasy, ky[i]); if(i == 1) addedge(cntx + i, t, lasy, 0); else addedge(cntx + i, cntx + i - 1, lasy, 0); } for(int i = 1; i <= n; i++) { addedge(q[i].tx, q[i].ty + cntx, 1, -q[i].id); } dinic(); printf("%lld ", -mincost); } return 0; }
