深入 聚集索引与非聚集索引(一)

有很多人写了聚集索引和非聚集索引的文章，但我觉得在很多文章中表达的概念并不清楚，因此自己也写一篇，能够让自己想清楚。我的最初目的是要写到NO SQL，因此这系列的文章主要是关注在 1.数据库索引结构、2.表联接、3.递归查询这几个点上。

一、基本概念

1.数据的读取

页(page)是SQL SERVER可以读写的最小I/O单位。即使只需访问一行,也要把整个页加载到缓存之中，再从缓存中读取数据。物理读取是从磁盘上读取，逻辑读取是从缓存中读取。物理读取一页的开销要比逻辑读取一页的要大得多。

2.表的组织方式

表有两种组织方式，B树(Balance Tree)或者堆(Heap)。当在表上创建了一个聚集索引的时候，整个表数据就以B数的结构排列。否则就是按照堆的结构排列。无论表是怎么组织的，都可以在表上面创建多个非聚集索引。非聚集索引都是以B树的结构排列。

2.1 堆（Heap）

之所以这个结构称为堆，是因为它不以任何人为指定的逻辑顺序进行排列。而是按照分区组队数据进行组织。也就是说，是按照磁盘的物理顺序。只要需要读取的数据文件没有文件系统碎片（注意和下面提到的索引的碎片区分），这个读取过程在磁盘中就可以连续的进行，没有多余的磁盘臂移动。而磁盘臂移动是I/O操作中开销最大的操作。

堆使用一个bitmap结构来管理数据的分配。也就是它会告诉你两个结果，这个区是分配了，还是没有分配。每一个区中的物理顺序如下图。

对于新插入的数据，堆只管在最后一条数据的后面的一个空闲位置保存新插入的数据，不保持任何的逻辑顺序。比如拿order表举例，如果先插入orderid 4,5,6, 假设在位置1:176、 1:177、1:178这三个位置。这时再插入1，这时保存的数据就变味4,5,6,1,  1保存在 1:179的位置。

2.2聚集索引（Clustered Index）

聚集索引以B树的方式保存数据。由于在另一篇文章中已经详细的分析了B树，这里就不再详细说明。

继续拿Order表举例，Order表中的全部数据都保存在B树中的叶层（leaf level）中，其他层只是起到一个索引的作用，并不包含任何数据。叶层是一个双向链表结构，并按照聚集索引的主键的逻辑顺序排列。因此逻辑顺序是用指针来维护。

我们在图中页层所见到是逻辑顺序，和上图堆中所展示的物理顺序要区分开来。

为什么我一再强调逻辑顺序和物理顺序？因为理解这很重要。

如图所示，聚集索引中除了B树之外，仍然维护了一个IAM结构，而这个结构就能保证在需要的时候，我们能按照物理顺序而不是逻辑顺序去在叶层中读取数据。

那么什么时候才需要呢？先看什么是索引碎片。

2.2.1 索引碎片

数据库中之所以会出现碎片，是因为B树的页拆分造成的。具体页拆分请参考数据结构，这里要说的是由于拆分所产生的新页不保证一定就会在被拆分的页的后面，而是可能出于文件的任何位置。这就是“无序页”。换句话说，也就是在列表中处于后面位置的元素，在物理文件中却排在前面。如果你明白指针的定义的话，这句话并不难理解。因为叶层的双向列表就是以指针来维护逻辑顺序。

因此在按逻辑顺序读取的时候，由于无序页的存在，可能造成磁臂频繁的摆动。别忘记，磁盘摆动是I/O中开销最大的操作。而I/O往往是一个系统的瓶颈所在。

如果按照物理顺序来读取，也就是unordered读取，就会避免上面所产生的问题。再次强调，unordered是指不按逻辑顺序读取，所以叫unordered。

2.2.2 索引的层数

索引的层数，也就是B树的高度，直接表明了一次查找操作在页面读取方面的开销。一些执行计划如Nested loop联接会多次调用查找操作。因此理解这个概念很重要。

树的高度主要和以下几个因素相关

1. 表的总行数。
2. 平均一行保存数据的大小。
3. 页的平均密度。因为不是每一页都应该填充满数据，这样可以减少页拆分的次数。
4. 一页所能容纳的行数。

具体公式也很简单，3级索引大概能容纳4百万行，4级索引大概能容纳4亿行数据。因此通常一张表的索引层数通常为3到4级。

2.3非聚集索引(NonClustered Index)

非聚集索引也是以B树组织的。和聚集索引的区别就在于它的叶层并不包含所有的数据。在默认情况下它只包含了键列的数据，并包含了一个行定位符(row locator)。这个行定位符的具体内容取决于它建立在以堆形式的表还是以B树组织的表，换句话说也就是这张表是否建立了聚集索引会影响到非聚集索引的行定位符。如果是建立了聚集索引，那么这个行定位符就是一个聚集键，我们通过这个聚集键再次查找聚集索引上的数据。

 聚集索引上的非聚集索引

如果表是堆组织结构的，那么它就是一个直接指向数据所在行的物理指针。

下图是建立在堆上的非聚集索引

 

2.3.1 如果非聚集索引包含了我们需要查找的所有数据

这种情况我们通常叫做索引覆盖。

正因为非聚集索引有着和索引一样的结构，并且由于非聚集索引所包含的列少，因此数据量就小，使得叶层的一页能包含更多的行，因此进行一次I/O页读取的动作的时候，就能读取进更多的行。因此查找效率是最高的。

举个不恰当的例子，美女征婚，应征人员的个人信息表有 “姓名、 德、 智、 体 、美、 劳、 高、 富、 帅”这几列，按姓名排序。美女只关注“高、 富、 帅”这三列的内容，为了更快的筛选，我们帮美女按照个人信息表的内容重新制作了一张表，这张表忽略了其他信息，只保留了高、富、帅和姓名，筛选效率当然就比原来关注更多内容时要高。

2.3.2 如果非聚集索引不包含我们需要查找的所有数据

通俗的说这时我们就需要从非聚集索引中所包含的线索去包含所有数据的表中去找。

按照我们之前的定义换句话来说，就是通过非聚集索引中的行定位符去聚集索引或者堆中去查找所需的数据。

二、通过实例来说明上述概念

我们创建一张Order表，表上建立了几个索引

1.为orderdate列创建了聚集索引

2.为orderid列创建了非聚集索引

1.1.1 只为获取整张表的数据,对数据顺序不关心

SELECT [orderid]

      ,[custid]

      ,[empid]

      ,[shipperid]

      ,[orderdate]

      ,[filler]

  FROM [Performance].[dbo].[Orders]

分析：由于我们需要获取整张表的数据，因此不需要任何筛选也不需要任何排序。因此我们按照磁盘物理顺序读取出所有数据无疑是最快的选择。 所以已排序为False. 再次说明这里的顺序是聚集键的逻辑顺序，和物理顺序不同。

通过IAM在聚集索引的叶层扫描。在这种情况下无论表是以堆或者B树的形式组织情况都类似。

(1000000 行受影响)

表'Orders'。扫描计数1，逻辑读取25081 次，物理读取5 次，预读23545 次，lob 逻辑读取0 次，lob 物理读取0 次，lob 预读0 次。

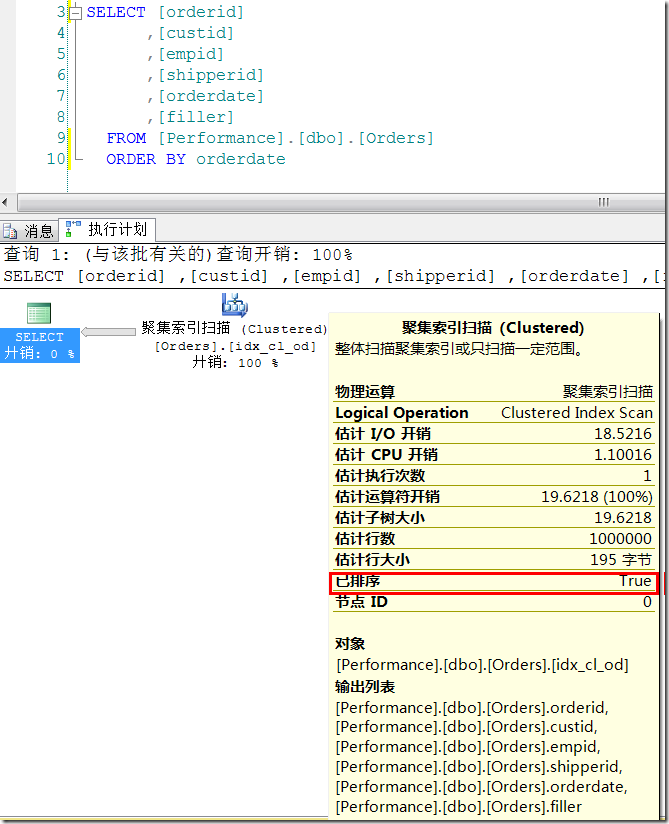
1.1.2 按聚集键顺序获取整张表的数据

对于Orders表，以orderdate为聚集键,因此如果我们使用顺序查询，就可以直接获取所需要的数据。

这是我们就不再通过IAM来对叶层进行扫描，而是通过叶节点的指针来进行扫描。

 

1.1.3 如果不按照聚集键，而是按照其他列的顺序来获取整张表

我们并没有把orderid设置成聚集索引的键，而是把它设成了非聚集索引的键。因此在返回整张表的内容时：

1.非聚集索引键列orderid对我们没有意义，因为我们期望返回的是整张表的内容，而非聚集索引只包含键列的内容。

2.聚集键列orderdate的顺序在这里对我们是没有什么用的。

由上面的推论可以知道，这时我们所创建的索引对我们都没有任何帮助。因此，与其按照逻辑顺序返回，不如按照最快速的无序返回，再把返回的结果集排序。而计划证明了我们的猜想。

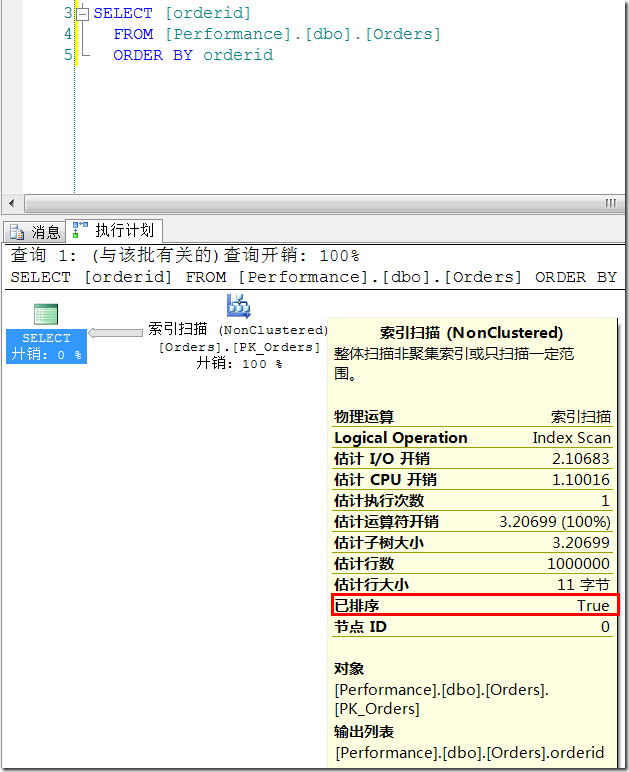
1.1.4 如果我们要查询的内容，正好在非聚集索引里面就已经包含了

和上面查询基本类似，区别在于我们在查询结果中把非聚集索引中不包含的列全部删除了，这时非聚集索引就形成了覆盖。我们就可以利用非聚集索引进行查询。

一些索引建议：
1.对于长字符串，比如VARCHAR(80)这种类型的索引要比更为紧凑数据类型的索引大很多。同样地，你也不太可能对长字符串列进行全匹配查找。

本来想一次写完，但是因为整体太长了，因此分开几段来写。

下一篇中我们将分析一些带有筛选条件WHERE的查询。

当然，如果觉得有帮助，请点一下推荐。