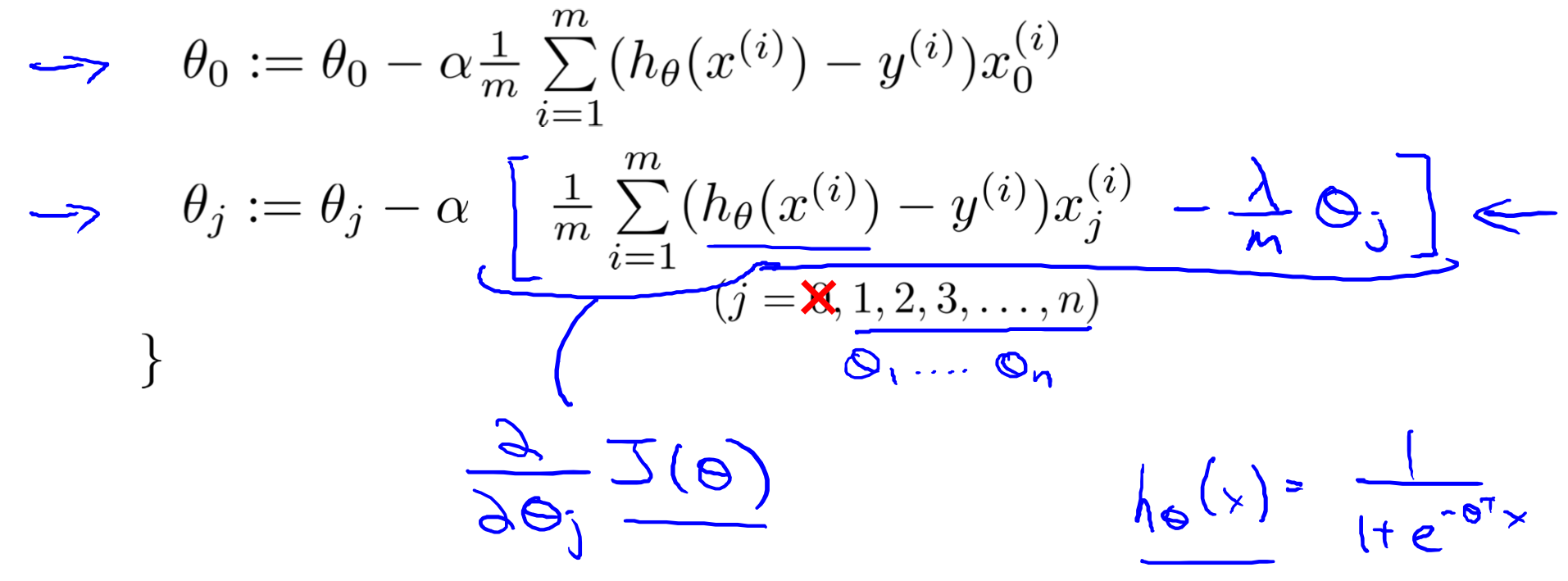机器学习笔记（8）：过拟合问题

过拟合问题

过拟合：当我们有太多的 feature 时， hypothesis 可能对训练集 fit 得非常好，但是对于新的测试数据可能会预测不准确。通常由生成了大量与数据无关的不必要曲线和角的复杂函数引起的。

欠拟合：明显有些数据不符合模型，通常由太简单的函数或者太少的 feature 引起的。

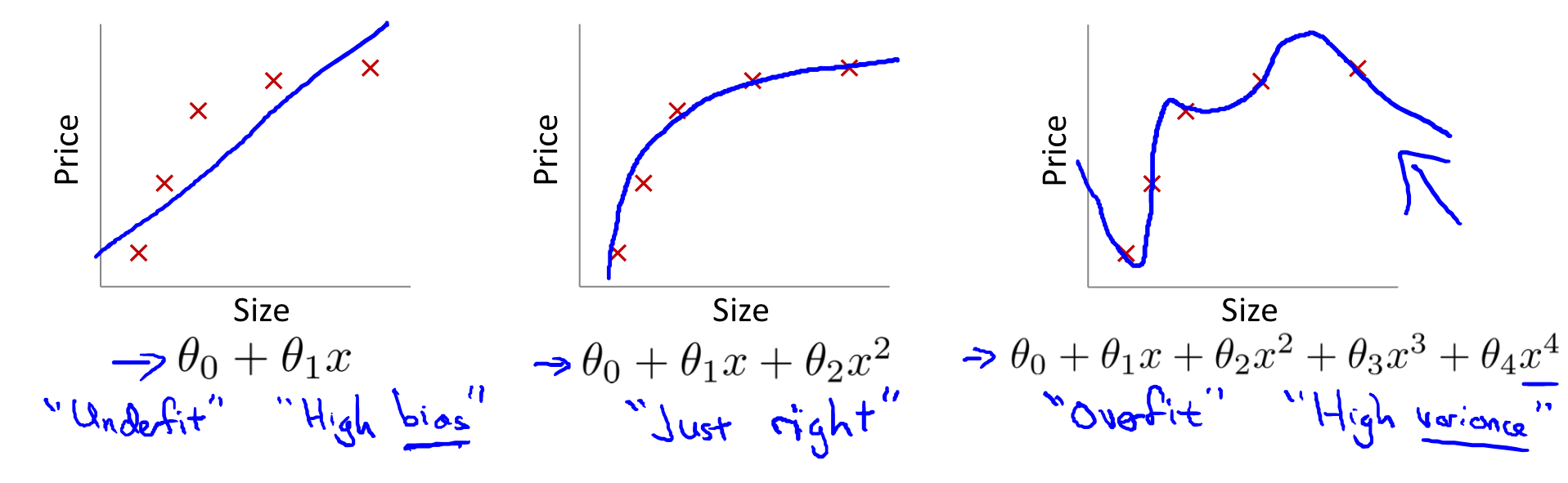
 下图是线性回归的过拟合和欠拟合： 

下图是逻辑回归的过拟合和欠拟合：

主要有两个方法来解决过拟合：

1）减少 feature 的数量：

     --- 手动选择留下哪些 feature

     --- 使用模型选择算法

2）正则化（Regularization）

     --- 保留所有的 feature，但是减少参数 θ_j 的量级

     --- 当我们有大量的有用的 feature时，正则化非常有效。

---

损失函数

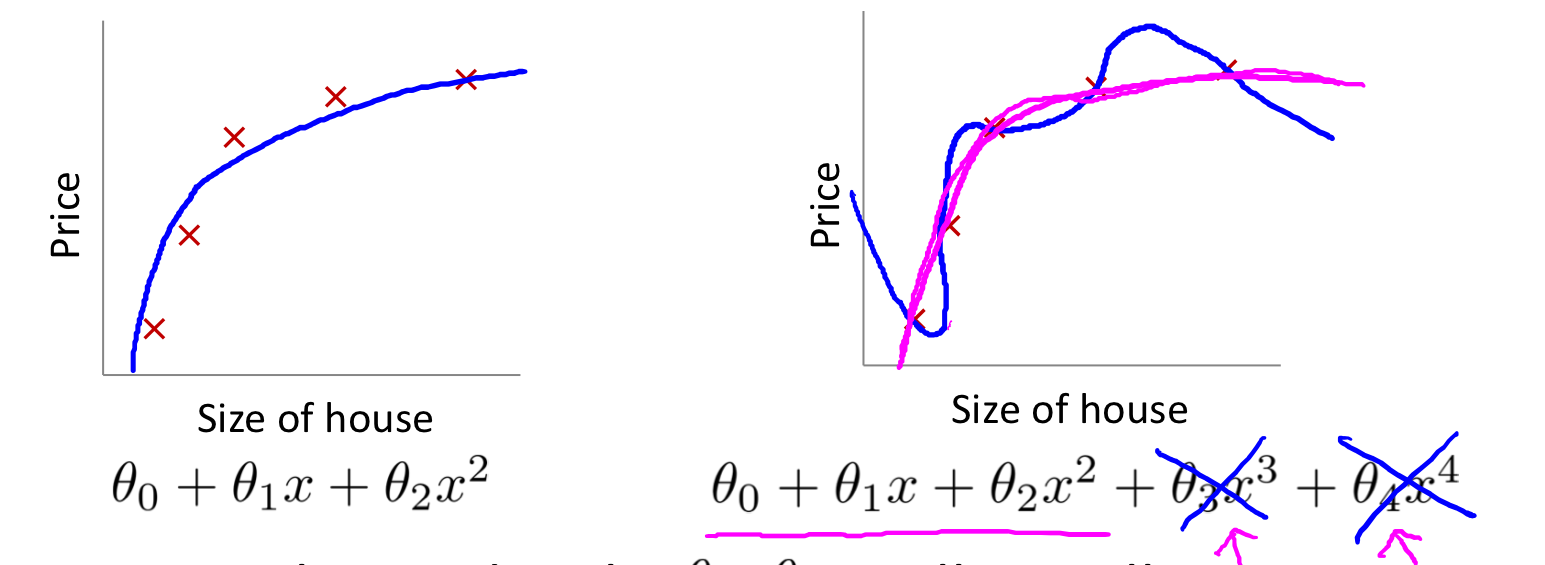
 如上图，为了消除后面两项的影响，在不去掉这些 feature 或者改变 hypothesis 的情况下，我们可以修改 cost function 为：

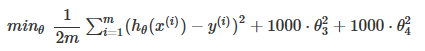
为了让 cost function 接近0，我们就需要减小 θ₃ 和 θ₄ 到接近0，这样新的 hypothesis 如红色线所示，可以更好的 fit  数据

我们可以正则化所有的 theta 参数：

其中， λ 就是正则化参数。用这个 cost function，我们就可以减少过拟合。但是，如果  λ  太大，可能会导致欠拟合。

---

正则化线性回归

梯度下降

梯度下降函数可以修改为：

变换后，也可以表示为：

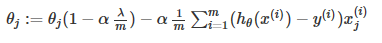
其中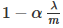，  总是小于1， 所以每次迭代都会减小 θ_j 的值。变换后，第二项和以前一样。

正规方程

 正规方程变换为：

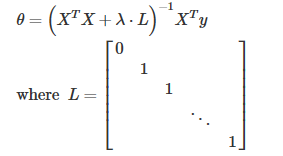
其中，L 是一个矩阵，矩阵的左上角为0，下面的对角线都为1，其余都为0，维度为 (n+1)x(n+1)。

在之前的视频中讲过，当 m<n 时， X^TX 是不可逆的。但是，这里当我们加入 λ·L 后，X^TX + λ·L 变为可逆的。

---

 正则化逻辑回归

类似线性回归

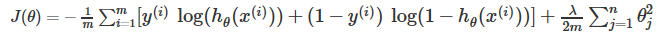
梯度下降：