学号20162320 《程序设计与数据结构》第1周学习总结
教材学习内容总结
- 算法效率,完成具体任务的算法效率是决定程序执行速度的一个主要因素,其中算法分析是计算机科学的基础课题。例如P292的洗盘子案例,两种不同的洗盘子方法,盘子越多,清洗的时间导致的差异越大。
- 增长函数和大O符号,增长函数表明了问题大小(n)与希望优化的值之间的关系,表示算法的时间复杂度或者空间复杂度,即显示了与问题大小相关的时间或空间利用率。其中重要的是算法的渐进复杂度(算法的阶),它由特性表达式(增长函数)的主项而定,而表示阶的记号成为O()。例如,t(n)=123,复杂度为O(1);t(n)=8n³+2n²,复杂度为O(n³)。总的来说算法的阶给出了算法增长函数的上界。
- 比较增长函数,处理器的速度和内存不能弥补算法效率的差异,例如具有n阶时间复杂度的算法A1改善了10倍,但具有n²阶时间复杂度的算法A2只改善了3.16倍,即10的平方根。
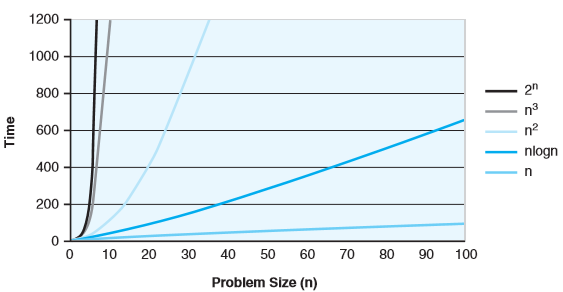
对于较小的n值,几个典型增长函数的比较 - 递归程序,经典案例:汉诺塔问题

解决n层盘子的汉诺塔问题,需要移动f(n)=2*(f(n-1+1)=2ⁿ-1次盘子,所以汉诺塔的复杂度是O(2ⁿ),虽然汉诺塔难题有指数阶的复杂度,效率非常低,但是它的实现很简洁。 - 大O符号实例理解,√{5n[3n(n+2)+4]+6}<√[5n(6n²+4)+6]<√(35n³+6)<6n1.5=O(n1.5),规则是
1.常系数可省略:O(f(n))=O(c×f(n))
2.低次项可忽略:O(na+nb)=O(n^a),a>b>0
对于对数O(logn)
1.常底数幂无所谓 ∀c>0,logn^c=clogn=O(logn)
2.常底数无所谓 ∀a,b>0,log_an=log_ab×log_bn=O(log_bn) - 图灵机TM,组成部分:
1.Tape,依次均匀地划分为单元格,各注有某一字符,默认为“#”
2.Alphabet,字符的种类有限
3.Head,总是对准某一单元格,并可以读取和改写其中的字符,每经过一个节拍,可转向左侧或右侧的邻格
4.State,图灵机总是处于有限种状态中的某一种,每经过一个节拍,可转向另一种状态
5.Transition Function:(q,c;d,L/R,p),若当前状态为q且字符为c,则将当前字符改写为d;转向右侧/左侧邻格;转入p状态,一旦转入待定的状态'h',则停机。
下图是我自己绘制的图灵机模型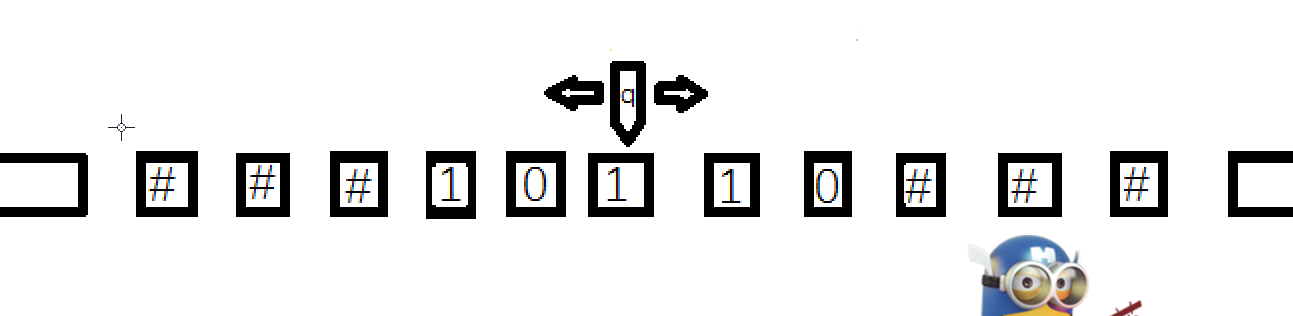
教材学习中的问题和解决过程
- 问题1:书上增长函数举例时例如t(n)=3logn,为什么没有底数?
解决过程:原来书上这么写时是为了举例,到了具体情况中就会有底数,是我多虑了。 - 问题2:
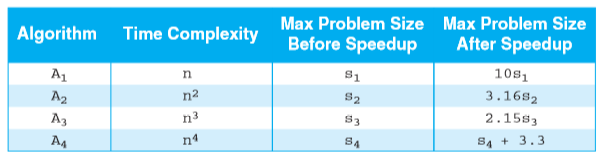
前面三个算法都很好理解,到A4就完全看不懂了。
解决过程:经王老师纠正,结果应为根号10,即3.16 - 问题3:为什么加快CPU的处理速度,并不一定能等量加快处理过程?
解决过程:线性加速仅发生在算法有限性阶O(n)的情况、当算法的复杂度增加时,更快的处理器的影响不如期望的大。
代码调试中的问题和解决过程
- 问题1:
for (int count=0; count < n; count++) {
for (int count2=0; count2 < n; count2=count2+2)
{
System.out.println(count, count2);
}
}
求该代码段的增长函数和阶
解决方案:通过和结对伙伴王彪的共同讨论,我们列出了当n=5时的所有情况,并进行整理。得出count = f(n)= n,count2 = g(n) = [ 1.当 n 为奇数,g(n) = n+1; 2.当n为偶数,g(n) = n]。
我们做了一个代码测试结果:
public class lxr {
public static void main(String[] args) {
int n = 8;
int count=0;
int count2=0;
for (count=0; count < n; count++) {
for ( count2=0; count2 < n; count2=count2+2)
{
System.out.println(count+","+count2);
}
}
System.out.println(count==n);
int num=n%2;
if (num==1){
System.out.println(count2==n+1);
System.out.println("ji");
}
else {
System.out.println(count2==n);
System.out.println("ou");
}
}
}
可知当n=8时,count=n应为ture,结果截图如下
代码托管
(statistics.sh脚本的运行结果截图)
上周考试错题总结
无
结对及互评
点评过的同学博客和代码
- 本周结对学习情况
其他(感悟、思考等,可选)
由于许久没有敲过代码,很多内容都感到生疏了。所以这一周除了完成老师要求的作业之外,更多的时间花在了复习以前的教材和以前做过的项目上面,争取把敲代码的感觉找回来。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 188 | 1/1 | 25 | 算法分析 |
| 第二周 | 1/2 |
- 计划学习时间: 15小时
- 实际学习时间: 25小时
(有空多看看现代软件工程 课件 软件工程师能力自我评价表)