实验涉及代码
Searching、BSTNode、Sorting、LinkedBinarySearchTree、Searchingtest、SortTest
查找与排序-1
实验目的:测试·Searching和Sorting.的方法,要求各种情况测试,排序需要正序和逆序
测试过程:
- 1.首先测试
Searching在数组依次中添加3、8、12、34、54、84、91、110、1、0十个元素
Comparable[] comparables = {1,0,3, 8, 12, 34, 54, 84, 91, 81,110};
- 2.测试二分查找的各种情况,首先测试数组中并未存在的45,然后测试数组中的54,即正常和异常的情况。由于该查找方法是返回值,所以预测结果应该为null与54,测试结果如下,测试成功。
Comparable result1 = Searching.binarySearch(comparables, 45);
System.out.println(result1);
Comparable result2 = Searching.binarySearch(comparables, 54);
System.out.println(result2 );

- 3.然后测试
Sorting方法,同样创建数字3, 12, 8, 34, 54, 84, 110, 91顺序不同的数组
Comparable[] lxr = {3, 12, 8, 34, 54, 84, 110, 91};
- 4.利用快速排序,每次比较都要把数据跟个成两个部分,将每次比较交换到左边的元素利用循环的Comparable方法提取出来,得到正序。利用冒泡排序,修改其中一部分源码为
if (data[scan].compareTo(data[scan + 1]) < 0),即通过比较将小的值放到右边,得到逆序。测试截图如下。
Sorting.quickSort(lxr, 0, lxr.length - 1);
for (Comparable lxrs : lxr) {
System.out.print(lxrs + " ");
}

查找与排序-2
实验目的:重构代码,在Idea和命令行两种方式运行
实验过程:
- 1.把
Sorting和Searching放入 cn.edu.besti.cs1623.刘先润2320包中,重新编译并运行。 - 2.实验结果见结果链接
查找与排序-3
实验目的:补充Searching的查找算法,并进行测试
实验过程:
- 0.所有查找算法都会测试正常和异常情况,查找所针对的数组是包含
3、8、12、34、54、84、91、110、1、0十个元素的。备注:树表查找是在二叉查找树中已经实现,不在赘述,可以参见我的代码 LinkedBinarySearchTree和 LinkedBinarySearchTreeTest - 1.插值查找(Interpolation Search)算法,是根据要查找的元素 key 与查找表中最大最小记录的关键字比较后的查找方法,其核心就在于插值的计算公式(key - a[low])/(a[high] - a[low])。我的实现思路是插值时将插入值比较数组中的中位数,如果比中位数小则继续比较中位数左边的数内部的中位数,依次查找,最后返回查找的值在数组中的下标。如果数组中没有此元素则返回不代表下标的值-1。
public static int interpolationSearch(int[] a, int key) {
int low, mid, high;
low = 0;// 最小下标
high = a.length - 1;// 最大小标
while (low < high) {
mid = low + (high - low) * (key - a[low]) / (a[high] - a[low]);
// mid = (high + low) / 2;// 折半下标
if (key > a[mid]) {
low = mid + 1; // 关键字比 折半值 大,则最小下标 调成 折半下标的下一位
} else if (key < a[mid]) {
high = mid - 1;// 关键字比 折半值 小,则最大下标 调成 折半下标的前一位
} else {
return mid; // 当 key == a[mid] 返回 折半下标
}
}
return -1;
}

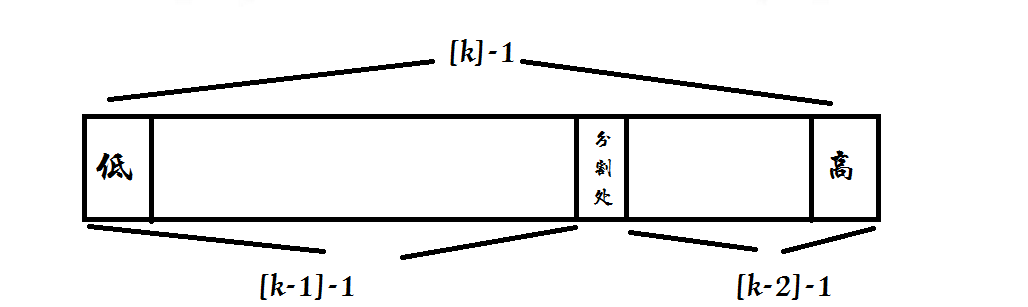
- 2.斐波那契查找(Fibonacci Search)算法,该算法和二分查找有些类似,不过二分查找是对半拆分进行查找,而斐波那契查找是根据黄金分割比例拆分的,而此处主要是用到了它的一条性质:前一个数除以相邻的后一个数,比值无限接近黄金分割。我的算法实现思路是当查找的元素key小于黄金分割位置元素,则继续查找前半部分,指针往大移动。令k为黄金分割值下标 ,f[k] = f[k-1] + f[k-2]((全部元素) = (前半部分)+(后半部分)),因为前半部分有f[k-1]个元素,则继续拆分f[k-1] = f[k-2] + f[k-3]成立 ,即在f[k-1]个元素的前半部分f[k-2]中继续查找,所以k = k - 1, 则下次循环mid = low + f[k - 1 - 1] - 1; 当查找的元素key大于黄金分割位置元素时,则查找后半部分,指针往小移动,因为后半部分有f[k-2]个元素, 则继续拆分f[k-2] = f[k-3] + f[k-4]成立,即在f[k-2]个元素的前半部分f[k-3]继续查找,所以k = k - 2,则下次循环mid = low + f[k - 2 - 1] - 1。如图所示
public static int fibonaciSearch(int[] b, int key) {
int[] f = {-1,0,3, 8, 12, 34, 54, 84, 91, 110};
int low1, mid1, high1, k;
low1 = 0;
high1 = b.length - 1;
k = 0;
while (high1 > f[k] - 1)
k++;
b = Arrays.copyOf(b, f[k]);
for (int i = high1 + 1; i < f[k]; i++) {
b[i] = b[high1];
}
while (low1 <=high1) {
mid1 = low1 + f[k - 1] - 1;
if (key < b[mid1]) {
high1 = mid1 - 1;
k = k - 1;
} else if (key > b[mid1]) {
low1 = mid1 + 1;
k = k - 2;
} else {
if (mid1 <= high1)
return mid1;
else
return high1;
}
}
return -1;
}

- 3.分块查找(BlockSearch)算法,分块查找是改进自折半查找和顺序查找的方法,把一个数据分为若干个块(一般按照大小区间来分),按照元素大小无序地放入块中,第n块中的每个元素一定比第n-1块中的任意元素大。我的实现思路:创建一个数组分为12个块容器,定义每个块的范围值,总块的范围值必须包含数组最大与最小值所包含的范围,利用二分查找的方法将元素进行比较并放入不同的块中。最后定义一个打印方法,根据分好的块,打印出每个块的元素及块索引,并打印出查找的元素在哪个块已经在块中的索引。
public static class BlockSearch {
private int[] index; //建立索引
private ArrayList[] list;
public BlockSearch(int[] index) {
if (index != null && index.length != 0) {
this.index = index;
this.list = new ArrayList[index.length];
for (int i = 0; i < list.length; i++) {
list[i] = new ArrayList();//初始化容器
}
} else {
throw new Error("index cannot be null or empty");
}
}
public void insert(int value) {
int i = binarysearch(value);
list[i].add(value);
}
private int binarysearch(int value) {
int start = 0;
int end = index.length;
int mid = -1;
while (start <= end) {
mid = (start + end) / 2;
if (index[mid] > value) {
end = mid - 1;
} else {
start = mid + 1;
}
}
return start;
}
public String search(int data) {
int i = binarysearch(data);
String q1="查无此数";
String q2="成功找到";
for (int j = 0; j < list[i].size(); j++) {
if (data == (int) list[i].get(j)) {
System.out.println(String.format("查找元素为第: %d块 第%d个 元素", i + 1, j + 1));
return q2;
}
}
return q1;
}
public void printAll() {
for (int i = 0; i < list.length; i++) {
ArrayList l = list[i];
System.out.print("块" + i + ":");
for (int j = 0; j < l.size(); j++) {
System.out.print(l.get(j) + " ");
}
}
}
}

- 4.哈希查找(HashSearch),是通过计算数据元素的存储地址进行查找的一种方法。哈希查找的本质是先将数据映射成它的哈希值,其主要难点在于构建一个哈希表。我的代码实现思路:首先利用给定的数组创建哈希表,通过建立函数将其元素保存在对应的地址中,在查找哈希表的过程中,当查找到这链表时,采用线性查找方法。如果两个元素经过计算所得到的哈希值相同,则在哈希表中为后插入的数据元素另外选择一个表项。当查找哈希表时,如果没有在第一个哈希表中找到该元素,程序就会继续往后查找,直到找到一个符合查找要求的数据元素,或者遇到一个空的表项。最后返回该元素在哈希表中的索引。
public static int searchHash(int[] hash, int hashLength, int key) {
int hashAddress = key % hashLength;
while (hash[hashAddress] != 0 && hash[hashAddress] != key) {
hashAddress = (++hashAddress) % hashLength;
}
if (hash[hashAddress] == 0)
return -1;
return hashAddress;}
public static void insertHash(int[] hash, int hashLength, int data) {
int hashAddress = data % hashLength;
while (hash[hashAddress] != 0) {
hashAddress = (++hashAddress) % hashLength;
}
hash[hashAddress] = data;
}

查找与排序-4
实验目的:补充实现希尔排序,堆排序,桶排序,二叉树排序并测试实现的算法(正常,异常,边界)
实验过程:
- 1.堆排序的排序于二叉树排序类似,利用堆顶记录的是堆中的最大这一特质,使得每次从无序中选择最大记录变得简单。堆排序是先将一组元素一项项地插入到堆中,然后一次删除一个,因为元素最先从堆中删除(在最大堆中),从堆中得到的元素序列将是有序序列,而且是降序的,类似地,一个最小堆可用来得到升序的排序结果。我的实现思路是首先初始建堆,array[0]为第一趟值最大的元素, 将堆顶元素和堆低元素交换,即得到当前最大元素正确的排序位置,最后将剩余的元素整理成堆。每次将堆的堆顶记录输出;同时调整剩余的记录,使他们重新排成一个堆。重复以上过程。
public int[] heapSort(int[] array){
array = buildMaxHeap(array);
for(int i=array.length-1;i>1;i--){
int temp = array[0];
array[0] = array[i];
array[i] = temp;
adjustDownToUp(array, 0,i);
}
return array;
}

- 2.二叉树排序,该排序方式是根据二叉排序树的性质——结点左孩子小于结点值、右孩子大于结点值来实现排序的。由于该算法在17章的教材中早就已经实现,所以就不多阐述。主要点在于在二叉排序树添加元素的操作,放入书中成为根结点并进行比较入左子树还是右子树的代码实现。
public void add (T item) {
if (item.compareTo(element) < 0)
if (left == null)
left = new BSTNode (item);
else
((BSTNode)left).add (item);
else
if (right == null)
right = new BSTNode (item);
else
((BSTNode)right).add (item);

- 3.桶排序工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序)。我的实现思路:根据数组的长度创建桶的数量,然后遍历数组,将数组的元素放入桶中,然后再排序桶,最后将桶中的元素打印出来。
public static void bucketSort(int[] arr){
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int i = 0; i < arr.length; i++){
max = Math.max(max, arr[i]);
min = Math.min(min, arr[i]);
}
//桶数
int bucketNum = (max - min) / arr.length + 1;
ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
for(int i = 0; i < bucketNum; i++){
bucketArr.add(new ArrayList<Integer>());
}
for(int i = 0; i < arr.length; i++){
int num = (arr[i] - min) / (arr.length);
bucketArr.get(num).add(arr[i]);
}
for(int i = 0; i < bucketArr.size(); i++){
Collections.sort(bucketArr.get(i));
}
System.out.println(bucketArr.toString());

- 4.希尔排序,是插入排序的改进方法,希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。我的实现思路将数组的元素放入一个初始数组中,然后将数组中每个元素对应其相隔n个索引的数组元素,进行比较大小,小的元素将其交换至左边,然后每完成一次操作索引数n递减,最后得到一个有序数列,并将其输出。
public static void shellSortSmallToBig(int[] data) {
int j = 0;
int temp = 0;
for (int increment = data.length / 2; increment > 0; increment /= 2) {
System.out.println();
for (int i = increment; i < data.length; i++) {
// System.out.println("i:" + i);
temp = data[i];
for (j = i - increment; j >= 0; j -= increment) {
if (temp < data[j]) {
data[j + increment] = data[j];
} else {
break;
}
}
data[j + increment] = temp;
}
for (int i = 0; i < data.length; i++)
System.out.print(data[i] + " ");
}
}
