支持向量机(support vector machines)是一个二分类的分类模型(或者叫做分类器)。如图:
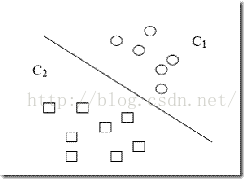
它分类的思想是,给定给一个包含正例和反例的样本集合,svm的目的是寻找一个超平面来对样本根据正例和反例进行分割。
各种资料对它评价甚高,说“ 它在解决小样本、非线性及高维模式识别中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中”
SVM之线性分类器
如果一个线性函数能够将样本完全正确的分开,就称这些数据是线性可分的,否则称为非线性可分的。
什么叫线性函数呢?在一维空间里就是一个点,在二维空间里就是一条直线,三维空间里就是一个平面,以此类推。
如果不关注空间的维数,这种线性函数就是前言中所说的那个统一的名称——超平面(Hyper Plane)!
在样本空间中,划分超平面可通过如下线性方程来描述:

假设它已经完成了对样本的分隔,且两种样本的标签分别是{+1,-1},那么对于一个分类器来说,g(x)>0和个g(x)<0就可以分别代表两个不同的类别,+1和-1。
但光是分开是不够的,SVM的核心思想是尽最大努力使分开的两个类别有最大间隔,这样才使得分隔具有更高的可信度。而且对于未知的新样本才有很好的分类预测能力(在机器学习中叫泛化能力)
那么怎么描述这个间隔,并且让它最大呢?SVM的办法是:让离分隔面最近的数据点具有最大的距离。
为了描述离分隔超平面最近的数据点,需要找到两个和这个超平面平行和距离相等的超平面:
H1: y = wTx + b=+1 和 H2: y = wTx + b=-1
如图所示:
在这两个超平面上的样本点也就是理论上离分隔超平面最近的点,是它们的存在决定了H1和H2的位置,支撑起了分界线,它们就是所谓的支持向量,这就是支持向量机的由来
有了这两个超平面就可以顺理成章的定义上面提到的间隔(margin)了
二维情况下 ax+by=c1和ax+by=c两条平行线的距离公式为:
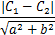
可以推出H1和H2两个超平面的间隔为2/||w||,即现在的目的是要最大化这个间隔。
所以support vector machine又叫Maximum margin hyper plane classifier
等价于最小化||w||

为了之后的求导和计算方便,进一步等价于最小化
假设超平面能将样本正确分类,则可令:
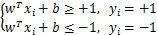
两个式子综合一下有:
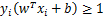
这就是目标函数的约束条件。现在这个问题就变成了一个最优化问题:
而且这是一个凸二次规划问题,一般的解决方法有两种1是用现成的优化工具包直接求解,2是使用Lagrange Duality找到一种更有效的方法求解。
其中方法2具有两个优点:
a、更好解
b、可以自然地引入核函数,推广到非线性分类
所以这里选用了第二种方法。
参考:https://blog.csdn.net/u012581541/article/details/51181041