T1 迷宫
- 【题目描述】
电脑游戏中有许多令人头疼的迷宫，会花费玩家相当多的时间，你通过秘笈获得了游戏迷宫的地图，你希望找到最短的一条走出迷宫的道路，并且想知道一共有多少条最短的道路，但是由于地图非常庞大，所以你不能在短时间找出这些道路，因此，你需要编写一个程序来找出这些最短的道路，并且统计一下一共有多少条这样的道路。
例如，对于下图所示的迷宫：
|
|
|
|
S |
|
|
X |
X |
|
|
|
X |
X |
|
|
E |
|
|
|
X表示障碍物，不可以通过，S表示迷宫的入口，E表示迷宫的出口。显然，从入口到出口至少需要走6步，而长度为6的道路一共有两条。
- 【输入文件】
输入文件maze.in，第一行是一个整数n（1 ≤n ≤ 25），表示迷宫是一个n×n的矩阵。以下n行每行有n个字符来描述地图，“.”表示可以通过，“X”表示不可以通过，“S”表示迷宫的入口，“E”表示迷宫的出口。（注意：所有的字母均为大写）。
- 【输出文件】
输出文件maze.out包括两行，第一行包含一个整数，表示从入口到出口走的最短距离。第二行包含一个整数，表示最短路径的条数，答案保证小于231。
- 【样例输入】
4
...S
.XX.
.XX.
E...
- 【样例输出】
6
2
1 /* 2 id:gww 3 language: 4 啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊 5 */ 6 #include<bits/stdc++.h> 7 using namespace std; 8 const int N=25+5; 9 int n,sx,sy,ex,ey,f[900][N][N],cnt; 10 char mp[N][N]; 11 int rd() 12 { 13 int x=0,w=0;char ch=0; 14 while(!isdigit(ch)) {w|=ch=='-';ch=getchar();} 15 while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); 16 return w?-x:x; 17 } 18 19 20 21 int main() 22 { 23 memset(f,0,sizeof(f)); 24 n=rd(); 25 for(int i=0;i<n;i++) 26 scanf("%s",mp[i]); 27 for(int i=0;i<n;i++) 28 for(int j=0;j<n;j++) 29 { 30 if(mp[i][j]=='S') sx=i,sy=j; 31 if(mp[i][j]=='E') ex=i,ey=j; 32 if(mp[i][j]=='X') cnt++; 33 } 34 f[0][sx][sy]=1;//初始化 35 for(int t=1;t<=n*n-cnt;t++) 36 { 37 if(f[t][ex][ey]) break; 38 for(int i=0;i<n;i++) 39 { 40 for(int j=0;j<n;j++) 41 { 42 if(mp[i][j]=='X'||!(f[t-1][i-1][j]+f[t-1][i+1][j]+f[t-1][i][j-1]+f[t-1][i][j+1])) continue; 43 f[t][i][j]=(f[t-1][i-1][j]+f[t-1][i+1][j]+f[t-1][i][j-1]+f[t-1][i][j+1]); 44 } 45 } 46 } 47 for(int t=0;t<=n*n-cnt;t++) 48 if(f[t][ex][ey]) {printf("%d %d ",t,f[t][ex][ey]);exit(0);} 49 return 0; 50 }
f[t][i][j]表示走t步到达(i,j) f[t][i][j]=f[t-1][i-1][j]+f[t-1][i+1][j]+f[t-1][i][j-1]+f[t-1][i][j+1]（即(i,j)的上下左右位置的方法数和）
但是不能直接f[t][i][j]=f[t-1][i-1][j]+f[t-1][i+1][j]+f[t-1][i][j-1]+f[t-1][i][j+1]，要用像走迷宫一样的来枚举上一步，要判断上一步判断是否合法，否则会出现从(0,j)或者从(n+1,j)等非法位置到达终点，QAQ然后导致爆炸
1 /* 2 id:gww 3 language: 4 啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊 5 */ 6 #include<bits/stdc++.h> 7 using namespace std; 8 const int N=25+5; 9 int n,sx,sy,ex,ey,f[900][N][N],cnt; 10 char mp[N][N]; 11 int dx[4]={0,0,1,-1}; 12 int dy[4]={1,-1,0,0}; 13 int rd() 14 { 15 int x=0,w=0;char ch=0; 16 while(!isdigit(ch)) {w|=ch=='-';ch=getchar();} 17 while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); 18 return w?-x:x; 19 } 20 21 int main() 22 { 23 memset(f,0,sizeof(f)); 24 n=rd(); 25 for(int i=0;i<n;i++) 26 scanf("%s",mp[i]); 27 for(int i=0;i<n;i++) 28 for(int j=0;j<n;j++) 29 { 30 if(mp[i][j]=='S') sx=i,sy=j; 31 if(mp[i][j]=='E') ex=i,ey=j; 32 if(mp[i][j]=='X') cnt++; 33 } 34 f[0][sx][sy]=1;//初始化 35 for(int t=1;t<=n*n-cnt;t++) 36 { 37 if(f[t][ex][ey]) break; 38 for(int i=0;i<n;i++) 39 for(int j=0;j<n;j++) 40 if(mp[i][j]!='X') 41 for(int k=0;k<4;k++) 42 { 43 int nx=i+dx[k],ny=j+dy[k]; 44 if(nx<0||ny<0||nx>n||ny>n||mp[nx][ny]=='X') continue; 45 f[t][i][j]+=f[t-1][nx][ny]; 46 } 47 } 48 for(int t=0;t<=n*n-cnt;t++) 49 if(f[t][ex][ey]) {printf("%d %d ",t,f[t][ex][ey]);exit(0);} 50 return 0; 51 }
随机找的一个大佬的搜索
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,dis[30][30],sx,sy,ex,ey,ans[30][30],tu[30][30]; 4 struct node{ 5 int x,y; 6 }; 7 int dx[4]={-1,0,0,1}; 8 int dy[4]={0,-1,1,0}; 9 queue<node>q; 10 void bfs() 11 { 12 node a; 13 a.x=sx; 14 a.y=sy; 15 q.push(a); 16 dis[sx][sy]=0; 17 ans[sx][sy]=1; 18 while(!q.empty()) 19 { 20 node u=q.front(); 21 q.pop(); 22 for(int i=0;i<4;i++) 23 { 24 int nx=u.x+dx[i]; 25 int ny=u.y+dy[i]; 26 if(!tu[nx][ny]) continue; 27 if(dis[nx][ny]>dis[u.x][u.y]+1) 28 { 29 dis[nx][ny]=dis[u.x][u.y]+1; 30 ans[nx][ny]=ans[u.x][u.y]; 31 q.push(node{nx,ny}); 32 } 33 else if(dis[nx][ny]==dis[u.x][u.y]+1) 34 ans[nx][ny]+=ans[u.x][u.y]; 35 } 36 } 37 } 38 39 int main() 40 { 41 //freopen("in.txt","r",stdin); 42 scanf("%d",&n); 43 memset(dis,127,sizeof(dis)); 44 char QAQ; 45 for(int i=1;i<=n;i++) 46 { 47 for(int j=1;j<=n;j++) 48 { 49 cin>>QAQ; 50 if(QAQ=='S') 51 tu[i][j]=1,sx=i,sy=j; 52 if(QAQ=='E') 53 tu[i][j]=1,ex=i,ey=j; 54 if(QAQ=='.') 55 tu[i][j]=1; 56 } 57 } 58 bfs(); 59 printf("%d %d",dis[ex][ey],ans[ex][ey]); 60 return 0; 61 }
T2 最大数列
- 题目描述
有一个N项的数列a1, a2 ... aN (|ai| <=10000, 1 <= i <= N)。S定义为
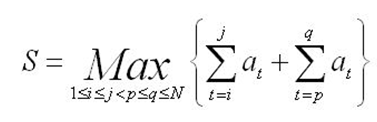
你的任务是求S的值，即为求一个序列的两个不相交连续子序列的最大和。
- 【输入文件】
输入文件sequence.in的第一行是一个整数N（2 <= N <= 100000），表示数列的项数。第二行有n个整数，用空格分隔，第i个整数Ai（|Ai| <=10000）是第i位数。
- 【输出文件】
输出文件sequence.out包括一行，这一行只包含一个整数，就是S。
- 【样例输入】
5
-5 9 -5 11 20
- 【样例输出】
40
- 【数据规模】
对于30%的数据，保证有n <= 80；
对于70%的数据，保证有n <= 10000；
对于全部的数据，保证有n <= 100000。
先看一个求一个最大子列的求法 从左往右枚举（我感觉没什么好解释的）
1 int sum=0,mi=0; 2 for(int i=1;i<=n;i++) 3 { 4 sum+=a[i]; 5 ans=max(ans,sum-mi); 6 mi=min(mi,sum); 7 }
然后两个子列不相交，我们就先从左往右求出左区间的最大子列 然后再从右往左求出右区间的最大子列 因为不相交 就加上f[i-1](配合下面代码食用)
1 /* 2 id:gww 3 language: 4 啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊 5 */ 6 #include<bits/stdc++.h> 7 using namespace std; 8 const int N=100000+10; 9 const int inf=0x3f3f3f3f; 10 int n,a[N],f[N],h[N],t[N];//前缀&&后缀 11 int rd() 12 { 13 int x=0,w=0;char ch=0; 14 while(!isdigit(ch)) {w|=ch=='-';ch=getchar();} 15 while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); 16 return w?-x:x; 17 } 18 19 int main() 20 { 21 n=rd();t[n+1]=h[0]=0; 22 for(int i=1;i<=n;i++) 23 { 24 a[i]=rd(); 25 h[i]=h[i-1]+a[i];//前缀 26 } 27 for(int i=n;i>0;i--) 28 t[i]=t[i+1]+a[i];//后缀 29 int mi=0;f[0]=-inf; 30 for(int i=1;i<=n;i++)//求左区间 31 { 32 f[i]=h[i]-mi; 33 f[i]=max(f[i],f[i-1]); 34 mi=min(mi,h[i]); 35 } 36 int ma=-inf,ans=-inf;mi=0; 37 for(int i=n;i>=2;i--) 38 { 39 ma=max(ma,t[i]-mi); 40 ans=max(ans,ma+f[i-1]);//加答案 41 mi=min(t[i],mi); 42 } 43 printf("%d",ans); 44 return 0; 45 }
T3 安装服务器
可以得两个结论
结论1：该点一定和某个坐标点重合（我记得证的时候很玄幻 好吧是我没听）
结论2：该点一定处于左权值之和刚好大于或者等于右权值之和的那个点。（这个很好证的）
然后就根据第一个结论就可以用枚举+递推推出来 预处理某个点到左边所有点的权值×距离差之和&这个点到右边所有点的权值×距离差之和
有了第二个结论 就相当于是找最优的x和y
1 /* 2 id:gww 3 language: 4 啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊 5 我不晓得对不对我只是有一个大胆的想法 6 */ 7 #include<bits/stdc++.h> 8 using namespace std; 9 const int N=100000+5; 10 int n,sum[N],ax,ay; 11 int rd() 12 { 13 int x=0,w=0;char ch=0; 14 while(!isdigit(ch)) {w|=ch=='-';ch=getchar();} 15 while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); 16 return w?-x:x; 17 } 18 19 struct lxyy 20 { 21 int x,y,w;//坐标 人口数*需求程度即权 22 }e[N]; 23 24 int cmp1(lxyy a,lxyy b)//排x坐标 25 { 26 return a.x<b.x; 27 } 28 int cmp2(lxyy a,lxyy b)//排y坐标 29 { 30 return a.y<b.y; 31 } 32 33 int main() 34 { 35 n=rd();sum[0]=0; 36 for(int i=1;i<=n;i++) 37 { 38 e[i].x=rd(),e[i].y=rd(); 39 int p=rd(),k=rd(); 40 e[i].w=p*k; 41 } 42 sort(e+1,e+1+n,cmp1); 43 for(int i=1;i<=n;i++) 44 sum[i]=sum[i-1]+e[i].w; 45 for(int i=1;i<=n;i++) 46 if((sum[i]>=sum[n]-sum[i])&&sum[i-1]<=sum[n]-sum[i-1]) 47 {ax=e[i].x;break;}//求中位数 48 sort(e+1,e+1+n,cmp2); 49 for(int i=1;i<=n;i++) 50 sum[i]=sum[i-1]+e[i].w; 51 for(int i=1;i<=n;i++) 52 if((sum[i]>=sum[n]-sum[i])&&sum[i-1]<=sum[n]-sum[i-1]) 53 {ay=e[i].y;break;} 54 printf("%d %d",ax,ay); 55 return 0; 56 }