最小生成树
所谓最小生成树,就是一个图的极小连通子图,它包含原图的所有顶点,并且所有边的权值之和尽可能的小。
首先看看第一个例子,有下面这样一个带权图:
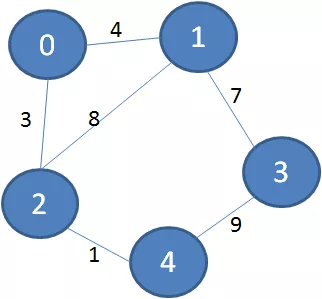
它的最小生成树是什么样子呢?下图绿色加粗的边可以把所有顶点连接起来,又保证了边的权值之和最小:
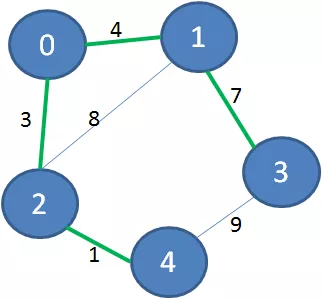
去掉那些多余的边,该图的最小生成树如下:
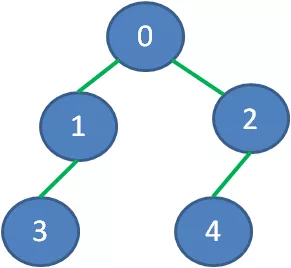
下面我们再来看一个更加复杂的带权图:
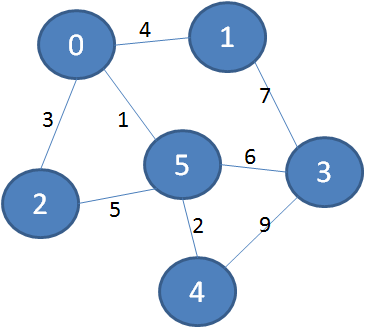
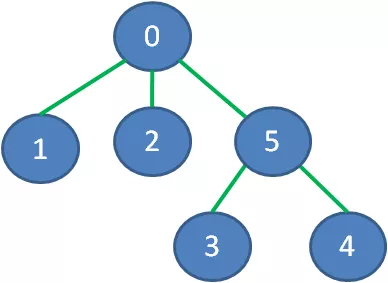
同样道理,下图绿色加粗的边可以把所有顶点连接起来,又保证了边的权值之和最小:

去掉那些多余的边,该图的最小生成树如下:
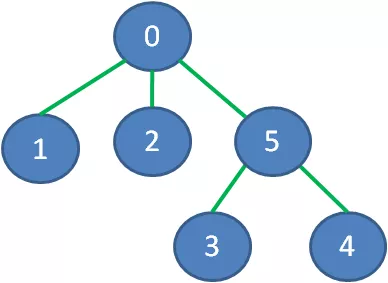
图的极小连通子图不需要回路,而是一个树形结构,所以人们才把它叫做最小生成【树】。图的最小生成树也不是唯一的,同一个图可以有多个不同的最小生成树,但是他们的权值之和是一样的。
最小生成树的用处可多了,比如我们要在若干个城市之间铺设道路,而我们的预算又是有限的,那么我们就需要找出成本最低的方式铺路,最小生成树的作用就来了。
怎样铺设才能保证成本最低呢?
城市之间的交通网就像一个连通图,我们并不需要在每两个城市之间都直接进行连接,只需要一个最小生成树,保证所有的城市都有铁路可以触达即可。

通常生成最小生成树常用的算法有两种,一种是 Kruskal 算法,另一种是 Prim 算法。下面介绍下 Prim 算法
Prim算法是如何工作的呢?
这个算法是以图的顶点为基础,从一个初始顶点开始,寻找触达其他顶点权值最小的边,并把该顶点加入到已触达顶点的集合中。当全部顶点都加入到集合时,算法的工作就完成了。Prim算法的本质,是基于贪心算法。
接下来说一说最小生成树的存储方式。我们最常见的树的存储方式,是链式存储,每一个节点包含若干孩子节点的指针,每一个孩子节点又包含更多孩子节点的指针:
这样的存储结构很清晰,但是也相对麻烦。为了便于操作,我们的最小生成树用一维数组来表达,数组下标所对应的元素,代表该顶点在最小生成树当中的父亲节点。(根节点没有父亲节点,所以元素值是-1)
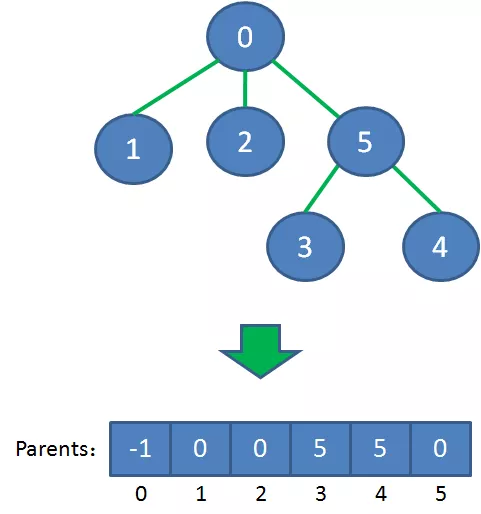
下面让我们来看一看算法的详细过程:
1.选择初始顶点,加入到已触达顶点集合。
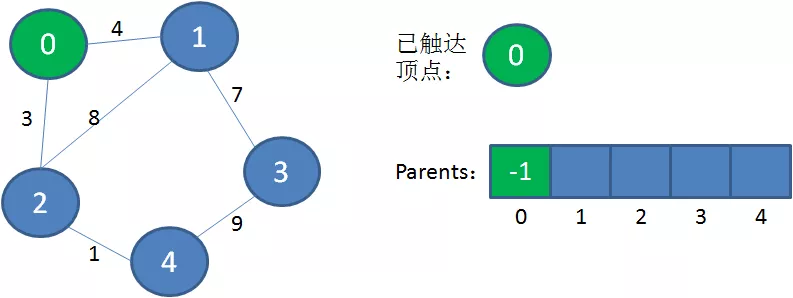
2.从已触达顶点出发,寻找到达新顶点的权值最小的边。显然从0到2的边权值最小,把顶点2加入到已触达顶点集合,Parents当中,下标2对应的父节点是0。

3.从已触达顶点出发,寻找到达新顶点的权值最小的边。显然从2到4的边权值最小,把顶点4加入到已触达顶点集合,Parents当中,下标4对应的父节点是2。
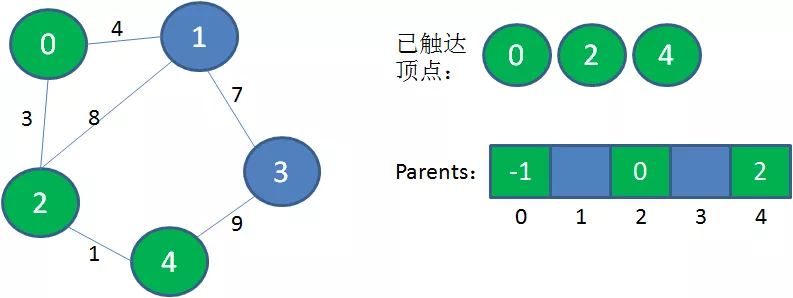
4.从已触达顶点出发,寻找到达新顶点的权值最小的边。显然从0到1的边权值最小,把顶点1加入到已触达顶点集合,Parents当中,下标1对应的父节点是0。

5.从已触达顶点出发,寻找到达新顶点的权值最小的边。显然从1到3的边权值最小,把顶点3加入到已触达顶点集合,Parents当中,下标3对应的父节点是1。
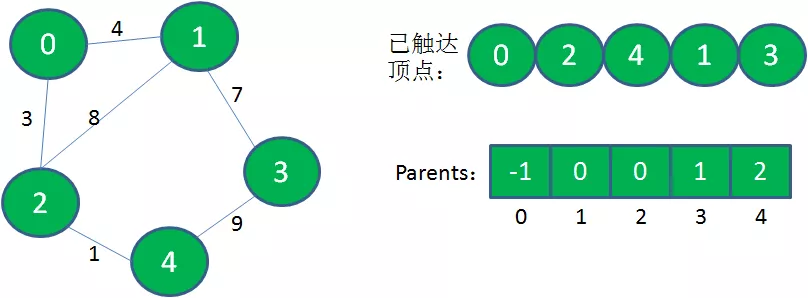
这样一来,所有顶点都加入到了已触达顶点集合,而最小生成树就存储在Parents数组当中。
Java:
import java.io.*; import java.util.*; class Test { final static int INF = Integer.MAX_VALUE; public static int[] prim(int[][]matrix){ List <Integer> reachedVertexList = new ArrayList<Integer>();
//选择顶点0为初始顶点,放入已触达顶点集合中 reachedVertexList.add(0);
//创建最小生成树数组,首元素设为-1 int[] parents = new int[matrix.length]; parents[0]=-1;
//边的权重 int weight;
//源顶点下标 int fromIndex = 0;
//目标顶点下标 int toIndex =0; while(reachedVertexList.size() < matrix.length){ weight =INF;
//在已触达的顶点中,寻找到达新顶点的最短边 for(Integer vertexIndex :reachedVertexList){ for(int i =0;i <matrix.length;i++){ if(!reachedVertexList.contains(i)){ if(matrix[vertexIndex][i]<weight){ fromIndex =vertexIndex; toIndex =i; weight =matrix[vertexIndex][i]; } } } } //确定了权值最小的目标顶点,放入已触达顶点集合 reachedVertexList.add(toIndex);
//放入最小生成树的数组 parents[toIndex]=fromIndex; } return parents; } public static void main(String[]args){ int[][]matrix =new int[][]{ {0,4,3,INF,INF}, {4,0,8,7,INF}, {3,8,0,INF,1}, {INF,7,INF,0,9}, {INF,INF,1,9,0}, }; int[]parents =prim(matrix); System.out.println(Arrays.toString(parents)); } }
运行结果:
[-1, 0, 0, 1, 2]
这段代码当中,图的存储方式是邻接矩阵,在main函数中作为测试用例的图和对应的邻接矩阵如下:
