Codeforces Round #368 (Div. 2) Pythagorean Triples

 Pythagorean Triples

 

　　Katya studies in a fifth grade. Recently her class studied right triangles and the Pythagorean theorem. It appeared, that there are triples of positive integers such that you can construct a right triangle with segments of lengths corresponding to triple. Such triples are called Pythagorean triples.

For example, triples (3, 4, 5), (5, 12, 13) and (6, 8, 10) are Pythagorean triples.

Here Katya wondered if she can specify the length of some side of right triangle and find any Pythagorean triple corresponding to such length? Note that the side which length is specified can be a cathetus as well as hypotenuse.

Katya had no problems with completing this task. Will you do the same?

Input

　　The only line of the input contains single integer n (1 ≤ n ≤ 10⁹) — the length of some side of a right triangle.

Output

　　Print two integers m and k (1 ≤ m, k ≤ 10¹⁸), such that n, m and k form a Pythagorean triple, in the only line.

In case if there is no any Pythagorean triple containing integer n, print  - 1 in the only line. If there are many answers, print any of them.

Examples

Input

 

3

Output

 

4 5

Input

 

6

Output

 

8 10

Input

 

1

Output

 

-1

Input

 

17

Output

 

144 145

Input

 

67

Output

 

2244 2245

Note

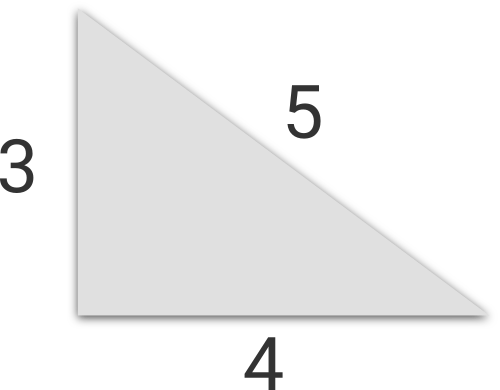
Illustration for the first sample.

题意：
　　给出一条直角边，求另外的两条边（都为整数）
思路：
　　公式推导题：
　　　　这要利用平方差公式
　　　　令斜边为c,直角边为a、b
　　　　c²-a²=(c+a)(c-a)
　　　　因此(c+a)(c-a)是完全平方数,且(c-a)是(c+a)的一个因数
　　　　1、如果(c-a)=1,则(c+a)是完全平方数（最短边是任意大于2的奇数）
　　　　例如：5、4、3；13、12、5；25、24、7；41、40、9；...
　　　　2、如果(c-a)=2,则(c+a)/2是完全平方数（最短边是任意大于2的偶数）
　　　　例如：5、3、4；10、8、6；17、15、8；26、24、10；...
　　　　即：最短边是任意一个大于2的正整数,都可以配成一个三边都是整数的直角三角形.
AC代码

# include <iostream>
using namespace std;
typedef long long int ll;
int main()
{
    ll n;
    while(cin >> n)
    {
        if(n <= 2)
            cout << "-1" << endl;
            
        else if(n % 2 == 1)
        {
            ll a = (n * n + 1) / 2;
            ll c = (n * n - 1) / 2;
            cout << c << " " << a << endl;
        }
        else
        {
            ll a = (n * n) / 4 + 1;
            ll c = (n * n) / 4 - 1;
            cout << c << " " << a << endl;
        }
    }
    return 0;
}