图的遍历，BFS和DFS的Java实现

1. BFS

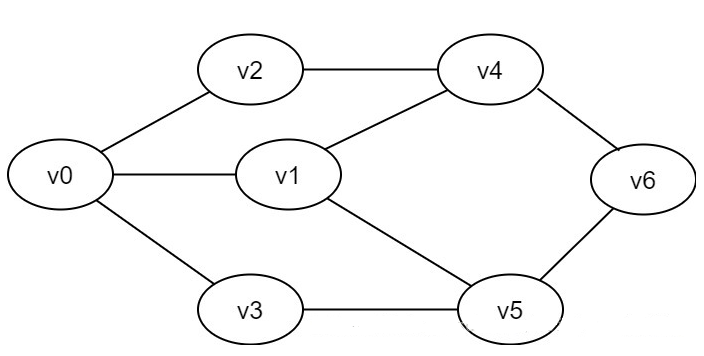
 广度优先搜索类似于树的层次遍历过程。它需要借助一个队列来实现。要想遍历从v0到v6的每一个顶点，我们可以设v0为第一层，v1、v2、v3为第二层（即先访问的第一个节点作为第一层，和第一个节点相连的邻接节点作为第二层），v4、v5为第三层，v6为第四层，再逐个遍历每一层的每个顶点。

具体实现：

（1）创建一个visited数组，用来记录已被访问过的顶点；创建一个队列，用来存放每一层的顶点；初始化图G。

（2）从图中的v0开始访问，将的visited[v0]数组的值设置为true，同时将v0入队。

（3）只要队列不空，则重复如下操作：队列顶点元素v0出队。依次检查v0的所有邻接节点w，如果visited[w]=false，则入队，并将visited[w]置为true

代码实现：

public class Solution {
//    用二维数组表示的无向图
    public List<Integer> Graph_BFS(int[][] graph){
//    构件一个图和一个visited，均用HashMap表示，List<Integer>表示和这个点直接相连的节点
        Map<Integer, List<Integer>> map = new HashMap<>();
        Map<Integer, Boolean> visited = new HashMap<>();
        for(int[] edge : graph){
            int from = edge[0];
            int to = edge[1];
            if(!map.containsKey(from)){
                map.put(from, new ArrayList<>());
            }
            if(!map.containsKey(to)){
                map.put(to, new ArrayList<>());
            }
            if(!visited.containsKey(from)){
                visited.put(from, false);
            }
            if(!visited.containsKey(to)){
                visited.put(to, false);
            }
            map.get(from).add(to);
            map.get(to).add(from);
        }
        List<Integer> nodes = new ArrayList<>();
        Queue<Integer> queue = new LinkedList<>();
//        随机选取一个开始节点
        int beginNode = graph[0][0];
        visited.put(beginNode, true);
        queue.add(beginNode);
        while(!queue.isEmpty()){
            int node = queue.poll();
            nodes.add(node);
            for(int connectedNode : map.get(node)){
                if(visited.get(connectedNode) == false){
                    queue.add(connectedNode);
//                    入队之后就把这个节点设为已访问
                    visited.put(connectedNode, true);
                }
            }
        }
        return nodes;
    }

    public static void main(String[] args) {
        //上图的无向图，以数字表示
        int[][] graph = new int[][]{{0,2}, {0,1}, {0,3}, {2,4}, {1,4}, {1,5}, {3,5}, {4,6}, {5,6}};
        System.out.println(new Solution().Graph_BFS(graph));
//        输出结果：[0, 2, 1, 3, 4, 5, 6]
    }
}

 2. DFS

深度优先搜索类似于树的先序遍历过程，需要借助一个栈来实现和一个boolean数组visited[]。要想遍历从v0到v6的每一个顶点，先把v0入栈，然后随机挑选一个和v0连接的visited为false的节点，入栈（每个节点入栈的时候，都要把这个节点的visited设为true）。

创建一个visited数组，用于记录所有被访问过的顶点。

具体实现：

1.从图中v0出发，访问v0。

2.找出v0的第一个未被访问的邻接点，访问该顶点。以该顶点为新顶点，重复此步骤，直至刚访问过的顶点没有未被访问的邻接点为止。

3.返回前一个访问过的仍有未被访问邻接点的顶点，继续访问该顶点的下一个未被访问领接点。

4.重复2,3步骤，直至所有顶点均被访问，搜索结束。

public List<Integer> Graph_DFS(int[][] graph){
        Map<Integer, List<Integer>> map = new HashMap<>();
        Map<Integer, Boolean> visited = new HashMap<>();
        for(int[] edge : graph){
            int from = edge[0];
            int to = edge[1];
            if(!map.containsKey(from)){
                map.put(from, new ArrayList<>());
            }
            if(!map.containsKey(to)){
                map.put(to, new ArrayList<>());
            }
            if(!visited.containsKey(from)){
                visited.put(from, false);
            }
            if(!visited.containsKey(to)){
                visited.put(to, false);
            }
            map.get(from).add(to);
            map.get(to).add(from);
        }
        List<Integer> nodes = new ArrayList<>();
        LinkedList<Integer> stack = new LinkedList<>();
        //        随机选取一个开始节点
        int beginNode = graph[0][0];
        visited.put(beginNode, true);
        stack.push(beginNode);
        while(!stack.isEmpty()){
            int node = stack.pop();
            nodes.add(node);
            for(int connectedNode : map.get(node)){
                if(!visited.get(connectedNode)){
                    stack.push(connectedNode);
                    visited.put(connectedNode, true);
                }
            }
        }
        return nodes;
    }

//        System.out.println(new Solution().Graph_DFS(graph));
//        输出结果：[0, 3, 5, 6, 4, 1, 2]