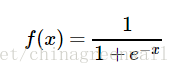机器学习-神经网络算法(二)

1. 关于非线性转化方程(non-linear transformation function)

     sigmoid函数(S 曲线)用来作为activation function:

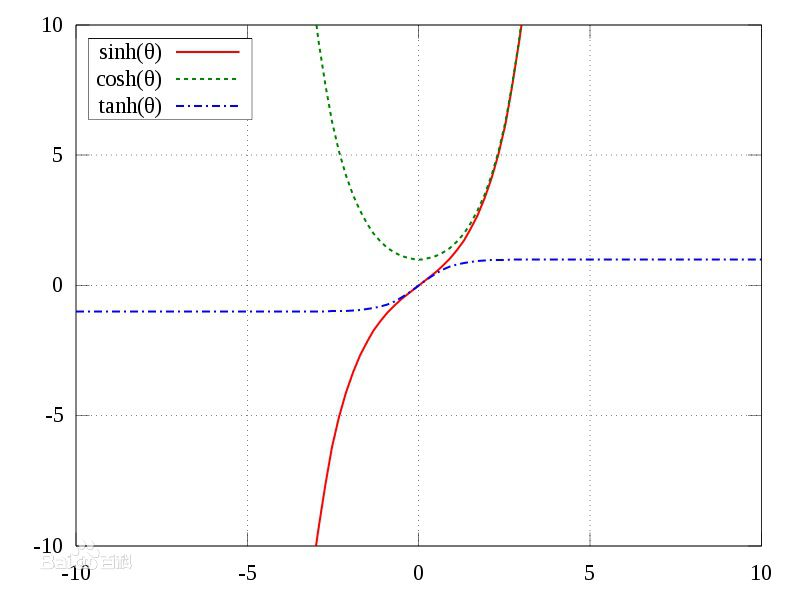
     sigmoid函数是一个在生物学中常见的S型函数，也称为S型生长曲线。 在信息科学中，由于其单增以及反函数单增等性质，sigmoid函数常被用作神经网络的阈值函数，将变量映射到0,1之间。具有这种性质的S型函数统称为sigmoid函数。

      

     1.1 双曲函数(tanh)

        双曲函数（hyperbolic function）可借助指数函数定义 

        双曲正弦：

               

        双曲余弦：

               

        双曲正切：

               

 

         导数：

 

          可以看到tanhx呈S型

     

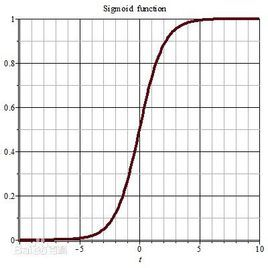
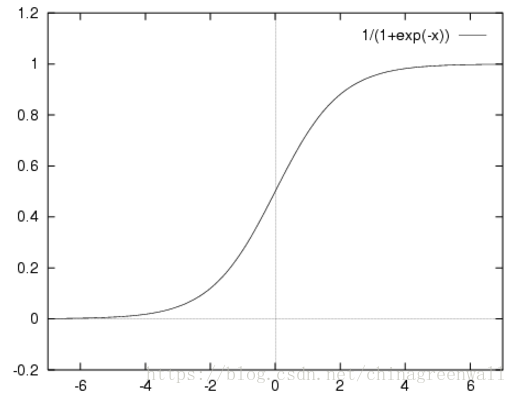
     1.2  逻辑函数(logistic function)

         其实logistic函数也就是经常说的sigmoid函数，它的几何形状也就是一条sigmoid曲线（S型曲线）。

                  

           导数：

                      

           

2. 手动实现一个简单的神经网络算法

# -*- coding:utf-8 -*-
import numpy as np


def tanh(x):
    return np.tanh(x)


def tanh_deriv(x):
    return 1.0 - np.tanh(x) * np.tanh(x)


def logistic(x):
    return 1 / (1 + np.exp(-x))


def logistic_deriv(x):
    return logistic(x) * (1 - logistic(x))


class NeuralNetwork:
    def __init__(self, layers, activation="tanh"):  # layers=[10,10,3]
        if activation == "logistic":
            self.activation = logistic
            self.activation_deriv = logistic_deriv
        elif activation == "tanh":
            self.activation = tanh
            self.activation_deriv = tanh_deriv
        # 随机产生权重[-0.25,+0.25]
        self.weights = []
        for i in range(1, len(layers) - 1):  # 产生(layers[i-1]+1,layers[i]+1) 如(3,2) 3行2列的随机数矩阵
            self.weights.append((2 * np.random.random((layers[i - 1] + 1, layers[i] + 1)) - 1) * 0.25)
            self.weights.append((2 * np.random.random((layers[i] + 1, layers[i + 1])) - 1) * 0.25)
            # print(str(self.weights))

    def fit(self, x, y, learning_rate=0.2, epochs=10000):
        x = np.atleast_2d(x)
        temp = np.ones([x.shape[0], x.shape[1] + 1])
        temp[:, 0:-1] = x
        x = temp
        y = np.array(y)

        for k in range(epochs):
            i = np.random.randint(x.shape[0])  # x.shape[0] is the number of the trainingset samples
            a = [x[i]]  # choose a sample randomly to train the model
            # print(str(a))
            for l in range(len(self.weights)):
                # print("a["+str(l)+"]; "+str(a[l])+"  WEIGHT "+str(self.weights[l])+str(len(self.weights)))
                a.append(self.activation(np.dot(a[l], self.weights[l])))  # a每个结点output值
            error = y[i] - a[-1]  # 误差 实际值-每个结点output值
            deltas = [error * self.activation_deriv(a[-1])]  # 对应输出层

            for l in range(len(a) - 2, 0, -1):
                # dot()函数可以通过numpy库调用，也可以由数组实例对象进行调用。
                # a.dot(b) 与 np.dot(a,b)效果相同。
                # deltas[-1].dot(self.weights[l].T) 等价于 dot(deltas[-1],self.weights[l].T)
                # deltas[-1] 对应上步的输出层
                deltas.append(deltas[-1].dot(self.weights[l].T) * self.activation_deriv(a[l]))  # 对于隐藏层
            deltas.reverse()

            for i in range(len(self.weights)):
                layer = np.atleast_2d(a[i])
                delta = np.atleast_2d(deltas[i])
                self.weights[i] += learning_rate * layer.T.dot(delta)  # layer.T.dot(delta)等价于dot(layer.T,delta)

    def predict(self, x):
        x = np.array(x)
        temp = np.ones(x.shape[0] + 1)
        temp[0:-1] = x
        a = temp
        for l in range(0, len(self.weights)):
            a = self.activation(np.dot(a, self.weights[l]))
        return a