BUAA软件工程个人项目

写在前面

项目	内容
所属课程	2020春季计算机学院软件工程(罗杰 任健) (北航)
作业要求	[个人项目作业](<https://edu.cnblogs.com/campus/buaa/BUAA_SE_2020_LJ/homework/10429)
课程目标	培养软件开发能力
本作业对实现目标的具体作用	锻炼个人开发项目的能力
教学班级	006
github项目地址	https://github.com/LiuZH-19/SE_IntersectProject

PSP表格记录

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	5	10
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	180	220
· Design Spec	· 生成设计文档	10	20
· Design Review	· 设计复审 (和同事审核设计文档)	15	20
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	5	5
· Design	· 具体设计	30	60
· Coding	· 具体编码	120	160
· Code Review	· 代码复审	20	20
· Test	· 测试（自我测试，修改代码，提交修改）	120	120
Reporting	报告
· Test Report	· 测试报告	30	30
· Size Measurement	· 计算工作量	5	5
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	10	30
	合计	550	700

解题思路描述

大体思路：

看了题目之后，想到的方法是：

• 利用数学的方法，解出两直线L1,L2存在交点的条件和其存在的交点的公式。

• 然后对输入中的任意两条直线，进行判断。若存在交点，则取出放入容器中(避免容器中元素的重复性)

• 最后输出容器中交点的个数

  但考虑到需对输入中的直线两两求解，复杂度为(O(n^2))。我打算上网查一查，看看有没有更巧妙的算法。

  查询无果，与小伙伴们讨论了一下，也没有更好的算法。就打算按这个算法，仔细想想细节部分。

  为了避免直线的一些特殊情况的分析，我即将直线表示为一般式：Ax+By+C=0

  附加题，也是类似的思路：

  直线两两求解交点，再求解直线之前的交点情况，再求解两圆之间的交点情况。

  在求解交点前，先判断是满足具有交点的条件，避免不必要的计算

细节考量：

直线与直线的交点比较好算，所以自己手算出来了算式关系。

直线与圆的公式也是手算的。

圆与圆之前的交点的公式，解得我头大，也不确定自己算出来的对不对，所以参考了网上的算法。详见

求任意两圆的交点

设计实现过程

代码组织：

期初设想：

• 类的设计：

  • Line 类
    • 直线用 Ax+By+C=0 表示 ，其中A,B,C为x1,y1,x2,y2的 函数
    • 属性为 A,B,C
    • 成员函数为 getA(), getB(), getC()
  • Circle类
    • 圆用((x-X)^{2}+(y-Y)^{2}=R^2)表示
    • 属性为 X, Y, R
    • 成员函数为 getX(), getY(),getR()

• 用 vector 存放 所有的直线

• 交点为Pair类型，用set存放所有的交点

• 三个函数，分别计算两直线之间，直线与圆之间，两圆之间的交点情况。

  按照上述思路实现后，我发现Line 和 Circle类有点多余。教材中也说，只是封装数据的话，不用class用struct。所以我打算将直线和圆的参数用结构体来存。将原先计算交点情况的三个函数封装成一个Calculator类。又考虑到计算中的精度损失问题，构造了point 类，重写了operator <。具体情况如下：

  后来改进：

• Calculator 类
  重载了三个成员函数

  class Calculator
  {
  public:
  	Calculator();
  	int haveIntersection(Line l1, Line l2, set<Point>& nodeSet);
  	int haveIntersection(Circle c, Line l, set<Point>& nodeSet);
  	int haveIntersection(Circle c1, Circle c2, set<Point>& nodeSet);
  };
  
  

• Point类
  自定义了运算符

  bool Point::operator < (const Point& p)const {
      //return x==p.x?y<p.y:x<p.x;
      return dcmp(x - p.x) == 0 ? dcmp(y - p.y) < 0 : dcmp(x - p.x) < 0;
  
  }
  
  bool Point::operator ==(const Point& p)const {
      if (dcmp(x-p.x)==0&&dcmp(y-p.y)==0)
          return true;
      return false;
  }
  

• Line 和Circle的架构体

• main中的函数 countALLinsect（）
  分别计算 直线之间，直线与圆之间，圆与圆之间的交点情况

单元测试设计

• 测试Calculator类，具体包括以下几个方面：
  • 直线直线的交点情况
    • 平行
    • 三线交于一点
    • 直线平行于x轴
    • 直线 平行于y轴
    • 一般情况
  • 直线与圆的交点情况
    • 直线的特殊情况
    • 线圆关系
      • 相切
      • 相离
      • 相交
  • 圆与圆的交点关系
    • 相离
    • 相交
    • 外切
    • 内切
    • 内含（同心）
  • 复杂情况（两圆与一直线）
    • 有一交点重叠
    • 有两个交点重叠
    • 一般情况
• 测试point类
  检测 重写的operator < 是否正确
• 整体测试
  • 大量数据测试 ，检测时间是否符合题意
  • 检测 set 是否去重

测试均通过，且交点为8000000左右时，用时7s，也没有超时。

性能改进相关

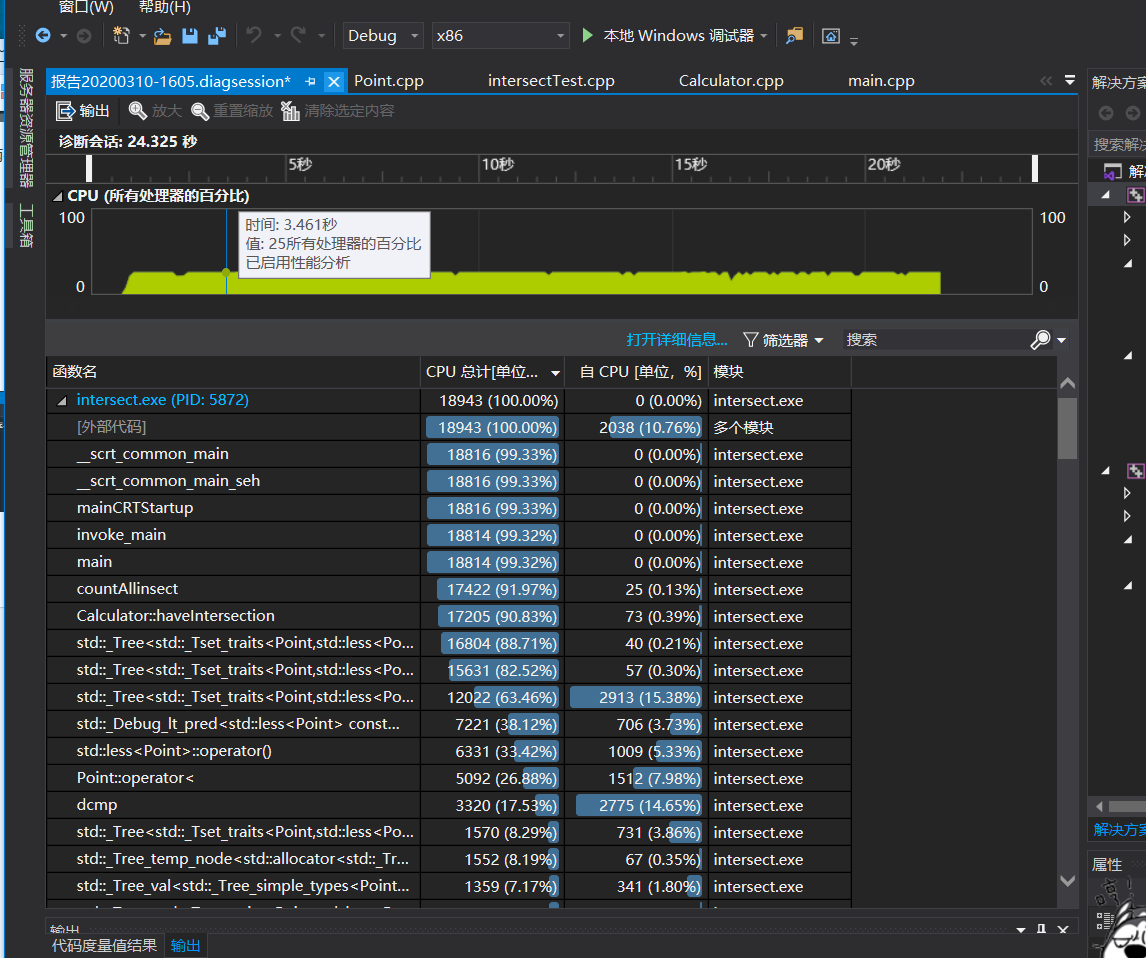
图中可以看出，采用set容器后，构建红黑树占用了绝大部分CPU时间。在建树过程中，用到了我在Point类里面 重写的operator <，故其占用时间也较多。除去set的相关操作外，接下来去看了下 Calculator中的函数。

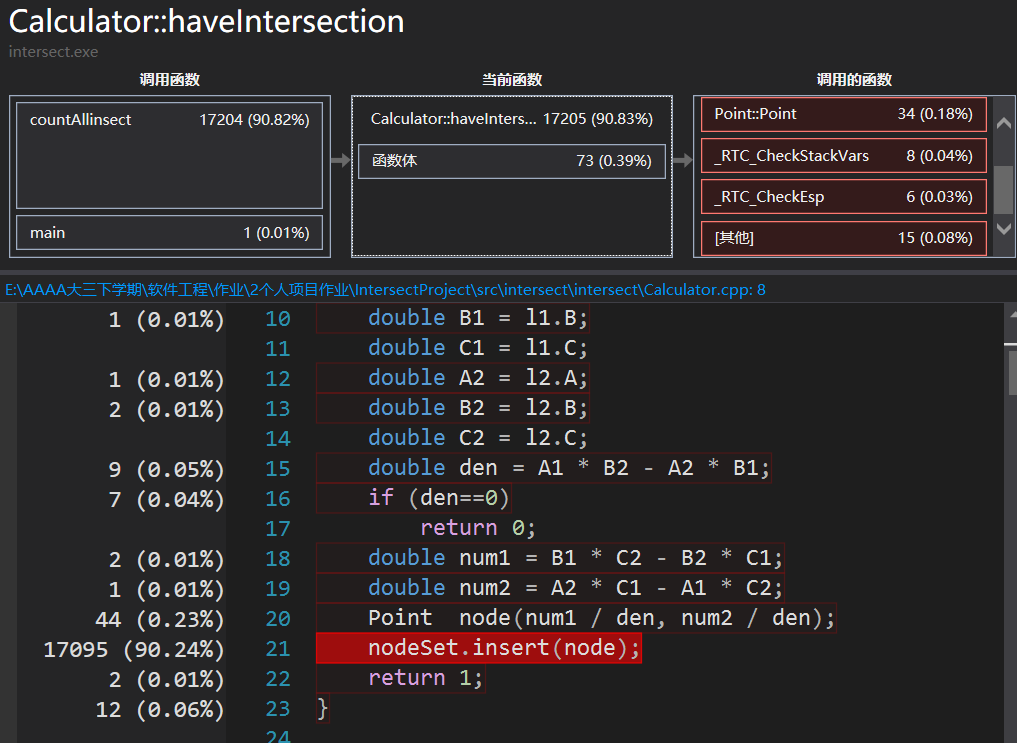
其中 CPU绝大部分的占用时间依然是 set的insert操作。所以在没能想到更优的算法下，性能改进工作可做的很少。我将一些常用的计算式先算出来，避免之后的重复计算。例如下图：

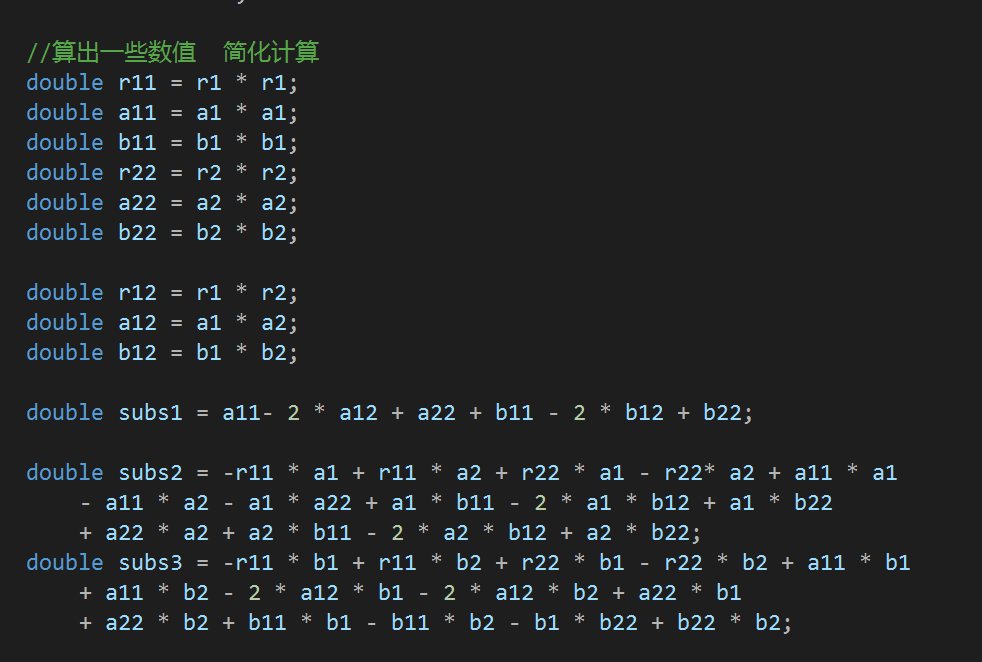
消除 Code Quality Analysis 中的所有警告

采用的是“Microsoft建议”的风格。

关键代码说明

• 求解所有的交点情况：直线之前、直线与圆、两圆之间

  int countAllinsect(vector<Line> lVec, vector<Circle> cVec, set<Point> &nodeSet){
      Calculator* calc = new Calculator();
      size_t i, j;
      //计算两条直线间的交点
      for (i = 0; i < lVec.size(); i++) {
          for (j = i + 1; j < lVec.size(); j++) {
              calc->haveIntersection(lVec[i], lVec[j], nodeSet);
          }
      }
      //计算直线与圆之间的交点
      for (i = 0; i < cVec.size(); i++) {
          for (j = 0; j < lVec.size(); j++) {
              calc->haveIntersection(cVec[i], lVec[j], nodeSet);
          }
      }
          //计算两圆之间的交点
      for (i = 0; i < cVec.size(); i++) {
          for (j = i + 1; j < cVec.size(); j++) {
              calc->haveIntersection(cVec[i], cVec[j], nodeSet);
          }
      }
      return nodeSet.size();
  }
  

  方法很暴力，就是循环遍历。

困惑

本次项目涉及到浮点数运算的精度问题。由于公式中存在开方以及除法运算，导致最终算出来的点只是近似值。因此我重写了 比较函数 ，EPS最终取的是0.0000001。虽然这个EPS是经过我多番测试选出来的值，但我任然无法保证他的实用性。所以在判断点是否重合的时候，可能会存在误差。

下面是关于精确度问题的相关代码：

#define EPS  0.0000001

int dcmp(double x) {
    if (fabs(x) < EPS) return 0;
    return x < 0 ? -1 : 1;
}

bool Point::operator < (const Point& p)const {
    //return x==p.x?y<p.y:x<p.x;
    return dcmp(x - p.x) == 0 ? dcmp(y - p.y) < 0 : dcmp(x - p.x) < 0;

}