原文地址:编程语言的可移植性 - kaizen - 博客园 (cnblogs.com)
【1】基数排序
以前研究的各种排序算法,都是通过比较数据大小的方法对欲排数据序列进行排序处理过程,而基数排序却不再相同。
那么,基数排序是采用怎样策略进行数据排序的呢?
简略概述:基数排序是通过“分配”和“收集”过程来实现排序。而这个思想该如何理解呢?请看以下例子:
(1)假设有欲排数据序列如下所示:
73 22 93 43 55 14 28 65 39 81
首先,根据每个数据个位数的数值,在遍历数据时将它们各自分配到编号0至9的桶(个位数值与桶号一一对应)中。
分配结果(逻辑想象)如下图所示:
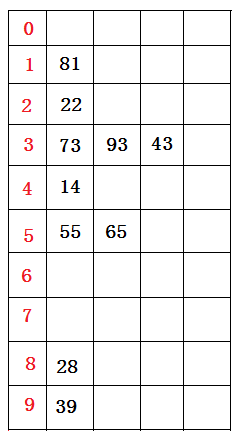
分配结束后。接下来将所有桶中(由顶至底)所盛数据按照桶号由小到大依次重新收集串起来,得到如下仍然无序的数据序列:
81 22 73 93 43 14 55 65 28 39
接着,再进行一次分配,这次根据每个数据十位数的数值来分配(原理同上),分配结果(逻辑想象)如下图所示:
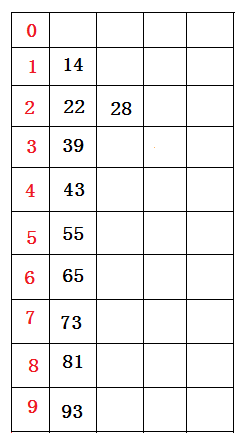
分配结束后。接下来再将所有桶中(由顶至底)所盛的数据(原理同上)依次重新再收集串接起来,得到如下的数据序列:
14 22 28 39 43 55 65 73 81 93
至此,观察可以看到:原无序数据序列已经变成有序的数据序列,即排序完毕。
如果排序的数据序列有三位数以上的数据,则重复进行以上的动作直至最高位数为止。
那么,到这里为止,你觉得自己是不是一个细心的人?不要不假思索的回答我。不论回答什么样的问题,都要做到心比头快,头比嘴快。
仔细看看你对整个排序的过程中还有哪些疑惑?真看不到?觉得我做得很好?抑或前面没看懂?
如果你看到这里真心没有意识到或发现这个问题,那我告诉你:悄悄去找个墙角蹲下用小拇指画圈圈(好好反省反省)。
追问:观察原无序数据序列中73 93 43 三个数据的顺序,在经过第一次(按照个位数值,它们三者应该是在同一个桶中)分配之后,
在桶中顺序由底至顶应该为73 93 43(即就是装的迟的在最上面,对应我们上面的逻辑想象应该是43 93 73),对吧?这个应该可以想明白吧?理论上应该是这样的。
但是、但是、但是分配后很明显在3号桶中三者的顺序刚好相反。这点难道你没有发现吗?或者是发现了觉得不屑谈及(算我贻笑大方)?
其实这个也正是基数排序稳定性的原因(分配时由末位向首位进行,即逆向遍历),请看下文的详细分析。
再思考一个问题:既然我们可以从最低位到最高位进行如此的分配收集,那么是否可以由最高位到最低位依次操作呢? 答案是完全可以的。
基于两种不同的排序顺序,我们将基数排序分为LSD(Least significant digital)或 MSD(Most significant digital),
LSD的排序方式由数值的最右边(低位)开始,而MSD则相反,由数值的最左边(高位)开始。
注意一点:LSD的基数排序适用于位数少的数列,如果位数多的话,使用MSD的效率会比较好。
MSD的方式与LSD相反,是由高位数为基底开始进行分配,但在分配之后并不马上合并回一个数组中,而是在每个“桶子”中建立“子桶”,将每个桶子中的数值按照下一数位的值分配到“子桶”中。
在进行完最低位数的分配后再合并回单一的数组中。
(2)我们把扑克牌的排序看成由花色和面值两个数据项组成的主关键字排序。
要求如下:
花色顺序:梅花<方块<红心<黑桃
面值顺序:2<3<4<...<10<J<Q<K<A
那么,若要将一副扑克牌排成下列次序:
梅花2,...,梅花A,方块2,...,方块A,红心2,...,红心A,黑桃2,...,黑桃A。
有两种排序方法:
<1> 先按花色分成四堆,把各堆收集起来;然后对每堆按面值由小到大排列,再按花色从小到大按堆收叠起来。----称为"最高位优先"(MSD)法。
<2> 先按面值由小到大排列成13堆,然后从小到大收集起来;再按花色不同分成四堆,最后顺序收集起来。----称为"最低位优先"(LSD)法。
【2】代码实现
(1)MSD法实现
最高位优先法通常是一个递归的过程:
<1> 先根据最高位关键码K1排序,得到若干对象组,对象组中每个对象都有相同关键码K1。
<2> 再分别对每组中对象根据关键码K2进行排序,按K2值的不同,再分成若干个更小的子组,每个子组中的对象具有相同的K1和K2值。
<3> 依此重复,直到对关键码Kd完成排序为止。
<4> 最后,把所有子组中的对象依次连接起来,就得到一个有序的对象序列。
示例代码如下:
1 #include <iostream>
2 #include <malloc.h>
3 using namespace std;
4
5 int getDigit(int x, int d)
6 {
7 int a[] = {1, 1, 10, 100}; // 因为待排数据最大数据也只是三位数,所以在此只需要到百位就满足
8 return ((x / a[d]) % 10); // 确定桶号
9 }
10
11 void printArr(int ar[], int n)
12 {
13 for (int i = 0; i < n; ++i)
14 {
15 cout << ar[i] << " ";
16 }
17 cout << endl;
18 }
19
20 void msdRadixSort(int arr[], int begin, int end, int d)
21 {
22 const int radix = 10;
23 int count[radix], i, j;
24 // 置空
25 for (i = 0; i < radix; ++i)
26 {
27 count[i] = 0;
28 }
29 // 分配桶存储空间
30 int *bucket = (int *)malloc((end - begin + 1) * sizeof(int));
31 // 统计各桶需要装的元素的个数
32 for (i = begin; i <= end; ++i)
33 {
34 count[getDigit(arr[i], d)]++;
35 }
36 // count[i]表示当前d位数值为i的桶底边界索引,即count[1]表示当前d位数值为1的桶底边界索引
37 // 或表示当前d位数值为(i+1)的桶顶索引,即count[1]表示当前d位数值为2的桶顶索引
38 for (i = 1; i < radix; ++i)
39 {
40 count[i] = count[i] + count[i - 1];
41 }
42 // 必须从右向左扫描
43 for (i = end; i >= begin; --i)
44 {
45 j = getDigit(arr[i], d); // 求出关键码第d位的数值。例如:576的第3位是((576 / 100) % 10) = 5
46 bucket[count[j] - 1] = arr[i]; // 放入对应的桶中,(count[j]-1)是当前d位数值为j的桶底索引
47 --count[j]; // 当前d位数值为j的桶底边界索引减一
48 }
49 // 注意:执行至此,count[i]表示当前d位数值为i的桶顶索引
50 // 从各个桶中收集数据
51 for (i = begin, j = 0; i <= end; ++i, ++j)
52 {
53 arr[i] = bucket[j];
54 }
55 // 释放存储空间
56 free(bucket);
57 // 对各个桶中的数据进行再排序
58 for (i = 0; i < radix; ++i)
59 {
60 int p1 = begin + count[i]; // 当前d位数值为i的桶顶索引
61 int p2 = 0; // 当前d位数值为i的桶底索引
62 if (i < radix - 1)
63 {
64 p2 = begin + count[i + 1] - 1;
65 }
66 else
67 {
68 p2 = end;
69 }
70 if (p1 < p2 && d > 1)
71 {
72 msdRadixSort(arr, p1, p2, d - 1); // 对桶递归调用,进行基数排序,数位降1
73 }
74 }
75 }
76
77 void main()
78 {
79 int ar[] = {20, 80, 90, 589, 998, 965, 852, 123, 456, 789};
80 int len = sizeof(ar) / sizeof(int);
81 cout << "排序前数据如下:" << endl;
82 printArr(ar, len);
83 msdRadixSort(ar, 0, len - 1, 3);
84 cout << "排序后结果如下:" << endl;
85 printArr(ar, len);
86
87 system("pause");
88 }
89
90 /*
91 排序前数据如下:
92 20 80 90 589 998 965 852 123 456 789
93 排序后结果如下:
94 20 80 90 123 456 589 789 852 965 998
95 请按任意键继续. . .
96 */
(2)LSD法实现
最低位优先法,首先依据最低位关键码Kd对所有对象进行一趟排序,
再依据次低位关键码Kd-1对上一趟排序的结果再排序,
依次重复,直到依据关键码K1最后一趟排序完成,就可以得到一个有序的序列。
使用这种排序方法对每一个关键码进行排序时,不需要再分组,而是整个对象组。
示例代码如下:
1 #include <iostream>
2 #include <malloc.h>
3 using namespace std;
4
5 int getDigit(int x, int d)
6 {
7 int a[] = {1, 1, 10, 100}; //最大三位数,所以这里只要百位就满足了。
8 return (x / a[d]) % 10;
9 }
10
11 void printArr(int ar[], int n)
12 {
13 for (int i = 0; i < n; ++i)
14 {
15 cout << ar[i] << " ";
16 }
17 cout << endl;
18 }
19
20 void lsdRadixSort(int arr[], int begin, int end, int d)
21 {
22 const int radix = 10;
23 int count[radix], i, j;
24
25 // 开辟所有桶的空间
26 int *bucket = (int *)malloc((end - begin + 1) * sizeof(int));
27
28 cout << "排序过程如下:" << endl;
29 // k == 1 表示个位数
30 // k == 2 表示十位数
31 // k == 3 表示百位数
32 for (int k = 1; k <= d; ++k)
33 {
34 // 置空
35 for (i = 0; i < radix; ++i)
36 {
37 count[i] = 0;
38 }
39 // 统计各个桶中所盛数据个数
40 for (i = begin; i <= end; ++i)
41 {
42 count[getDigit(arr[i], k)]++;
43 }
44 cout << ":: (k == " << k << ") ::" << endl;
45 printArr(count, radix);
46 // count[i]表示第k位数值为i的桶底边界索引,即count[1]表示第k位数值为1的桶底边界索引
47 // 或表示第k位数值为2的桶顶索引,即count[1]表示第k位数值为2的顶索引
48 for (i = 1; i < radix; ++i)
49 {
50 count[i] = count[i] + count[i - 1];
51 }
52 printArr(count, radix);
53 // 把数据依次装入桶(注意:装入时的分配技巧)
54 for (i = end; i >= begin; --i) // 必须从右向左扫描
55 {
56 j = getDigit(arr[i], k); // 求出关键码的第k位的数值, 例如:576的第3位是5
57 bucket[count[j] - 1] = arr[i]; // 放入对应的桶中,(count[j]-1)表示第k位数值为j的桶底索引
58 --count[j]; // 当前第k位数值为j的桶底边界索引减一
59 }
60 // 注意:执行至此,count[i]表示当前第k位数值为i的桶顶索引
61 printArr(count, radix);
62
63 // 从各个桶中收集数据
64 for (i = begin, j = 0; i <= end; ++i, ++j)
65 {
66 arr[i] = bucket[j];
67 }
68 printArr(arr, radix);
69 }
70
71 free(bucket);
72 }
73
74 void main()
75 {
76 int br[10] = {20, 80, 90, 589, 998, 965, 852, 123, 456, 789};
77 cout << "原数据如下:" << endl;
78 printArr(br, 10);
79 lsdRadixSort(br, 0, 9, 3);
80 cout << "排序后数据如下:" << endl;
81 printArr(br, 10);
82
83 system("pause");
84 }
85
86 /*
87 运行结果:
88 原数据如下:
89 20 80 90 589 998 965 852 123 456 789
90 排序过程如下:
91 :: (k == 1) ::
92 3 0 1 1 0 1 1 0 1 2
93 3 3 4 5 5 6 7 7 8 10
94 0 3 3 4 5 5 6 7 7 8
95 20 80 90 852 123 965 456 998 589 789
96 :: (k == 2) ::
97 0 0 2 0 0 2 1 0 3 2
98 0 0 2 2 2 4 5 5 8 10
99 0 0 0 2 2 2 4 5 5 8
100 20 123 852 456 965 80 589 789 90 998
101 :: (k == 3) ::
102 3 1 0 0 1 1 0 1 1 2
103 3 4 4 4 5 6 6 7 8 10
104 0 3 4 4 4 5 6 6 7 8
105 20 80 90 123 456 589 789 852 965 998
106 排序后数据如下:
107 20 80 90 123 456 589 789 852 965 998
108 请按任意键继续. . .
109 */
注意:以上两种方法,我们均使用数组模拟桶,关于数组模拟桶详细讲解请参考随笔《桶排序》
【3】基数排序稳定性分析
基数排序是稳定性排序算法。那么,到底如何理解它所谓的稳定特性呢?
(1)示例分析
比如:我们有如下欲排数据序列:
注意:在原始数据序列中,两个数据值相同(即12),而索引分别为1、4。
而所谓稳定性,即要求在排序完成后的有序数据序列中两个相同值的索引仍然是后者大于前者(最末数据12的索引值 > 第二个数据12的索引值)。

下面按LSD逻辑进行演示:
第一次,按个位数值分配。结果如下图所示:

然后,收集数据结果如下:

第二次,按十位数值分配。结果如下图所示:

然后,收集数据结果如下:

注意:分配时是从欲排数据序列的末位开始进行,逐次分配至首位。
(2)结果分析:
原始数据序列中相同数据值12的索引分别为1、4。
由最终的排序结果可看出:在有序数据序列中相同值(12)的索引分别为1、2。
很明显,原始数据序列中的最末位的12在有序数据序列中位置仍然居于原始数据序列中第二个数据值12之后(即按索引2 > 1)。
(3)如果从左向右扫描,同样的示例,依据LSD方法的规则,我们可以看到如下的排序过程:

显然,最终结果是无序的,这种扫描方式是错误的。所以,基数排序必须由后向前遍历原始数据序列。
排序结束。相信一定一目了然。
