问题描述
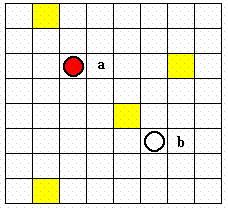
小鼠a与小鼠b身处一个m×n的迷宫中,如图所示。每一个方格表示迷宫中的一个房间。这m×n个房间中有一些房间是封闭的,不允许任何人进入。在迷宫中任何位置均可沿上,下,左,右4个方向进入未封闭的房间。小鼠a位于迷宫的(p,q)方格中,它必须找出一条通向小鼠b所在的(r,s)方格的路。请帮助小鼠a找出所有通向小鼠b的最短道路。
编程任务
对于给定的小鼠的迷宫,编程计算小鼠a通向小鼠b的所有最短道路。
输入:
本题有多组输入数据,你必须处理到EOF为止。
每组数据的第一行有3个正整数n,m,k,分别表示迷宫的行数,列数和封闭的房间数。接下来的k行中,每行2个正整数,表示被封闭的房间所在的行号和列号。最后的2行,每行也有2个正整数,分别表示小鼠a所处的方格(p,q)和小鼠b所处的方格(r,s)。(1≤p,r≤n; 1≤q,s≤m)
输出:
对于每组数据,将计算出的小鼠a通向小鼠b的最短路长度和有多少条不同的最短路输出。每组数据输出两行,第一行是最短路长度;第2行是不同的最短路数。每组输出之间没有空行。
如果小鼠a无法通向小鼠b则输出“No Solution!”。
Input
8 8 3
3 3
4 5
6 6
2 1
7 7
Output
11
96
分析:利用bfs可以计算出最短路径的距离len(即移动次数),然后用dfs计算出等于len(移动次数)时有多少种不同的最短路径。
代码:
#include<bits/stdc++.h>
using namespace std;
struct node
{
int x,y,s;
};
node que[2000];
int flag,ans,counta=0,next[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
int n,m,k,an,bn,sx,sy,q,p,tx,ty,a[51][51],vis[51][51],vis1[51][51];;
int bfs()
{
int head=1;
int tail=head;
que[tail].x=sx;
que[tail].y=sy;
que[tail].s=0;
tail++;
vis[sx][sy]=1;
flag=0;
while(head<tail)
{
for(int h=0;h<4;h++)
{
tx=que[head].x+next[h][0];
ty=que[head].y+next[h][1];
if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&a[tx][ty]==0&&vis[tx][ty]==0)
{
vis[tx][ty]=1;
que[tail].x=tx;
que[tail].y=ty;
que[tail].s=que[head].s+1;
tail++;
}
if((tx==p)&&(ty==q)) return que[tail-1].s;
}
head++;
}
}
void dfs(int x,int y,int step)
{
int tx,ty,k;
if(x==p&&y==q&&step==ans)
{
counta++;
return ;
}
if(step>ans) return ;
for(k=0;k<4;k++)
{
tx=x+next[k][0];
ty=y+next[k][1];
if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&a[tx][ty]==0&&vis1[tx][ty]==0)
{
vis1[tx][ty]=1;
dfs(tx,ty,step+1);
vis1[tx][ty]=0;
}
}
}
int main()
{
cin>>n>>m>>k;
for(int i=1;i<=k;i++)
{
cin>>an>>bn;
a[an][bn]=1;
}
cin>>sx>>sy>>p>>q;
cout<<"最短路径长度"<<(ans=bfs())<<endl;
dfs(sx,sy,0);
cout<<"最短路径条数"<<counta<<endl;
return 0;
}