一、二叉查找树
二叉查找树(Binary Search Tree,下文简称 BST)是一种二叉树的树形数据结构。
树上的每个节点带有一个数值,称为节点的“关键码”(也可以叫其他的 QAQ)。对于树中的任意一个节点:
- 该节点的关键码不小于它的左子树中任意节点的关键码。
- 该节点的关键码不大于它的右子树中任意节点的关键码。
即左子树任意节点的值 (<) 根节点的值 (<) 右子树任意节点的值。
满足上述性质的二叉树就是一棵 BST。显然,BST 的中序遍历是一个关键码单调递增的节点序列。
二、基本操作
约定:(lc(u)) 和 (rc(u)) 分别表示节点 (u) 的左子节点和右子节点,(val(u)) 表示节点 (u) 的关键码。
1. BST 的建立
为了避免越界,减少边界情况的判断,我们在 BST 中额外插入关键码为 (+infty) 和 (-infty) 的节点。仅由这两个节点构成的 BST 就是一棵初始的空 BST。
简便起见,在接下来的操作中,假设 BST 不含有关键码相同的节点。
int tot,rt,lc[N],rc[N],val[N]; //rt 为根结点在数组中的下标,lc(u) 和 rc(u) 分别表示 u 的左右子节点在数组中的下标,val(u) 表示节点 u 的关键码 void build(){ val[++tot]=-1e18,val[++tot]=1e18; //新建关键码为负无穷和正无穷的节点(它们在数组中的下标分别为 1、2) rt=1,rc[1]=2; //1 为根结点(对应关键码为负无穷的节点),它的右儿子为关键码为正无穷的节点 }
2. BST 的检索
在 BST 中检索是否存在关键码为 (k) 的节点。
设 (p) 为根结点,执行以下过程:
-
若 (val(p)=k),则已找到。
-
若 (val(p)>k):若 (lc(p)) 为空,则不存在 (k);否则,在 (p) 的左子树中递归进行检索。
-
若 (val(p)<k):若 (rc(p)) 为空,则不存在 (k);否则,在 (p) 的右子树中递归进行检索。
int find(int p,int k){ if(!p) return 0; //检索失败 if(val[p]==k) return p; //检索成功 return k<val[p]?find(lc[p],k):find(rc[p],k); }
3. BST 的插入
在 BST 中插入一个关键码为 (k) 的节点。(假设目前 BST 中不存在关键码为 (k) 的节点)
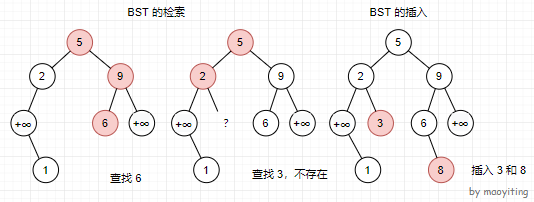
与 BST 的检索类似。要走向的 (p) 的子节点为空,说明 (k) 不存在时,直接建立关键码为 (k) 的新节点作为 (p) 的子节点。
void insert(int &p,int k){ if(!p){val[++tot]=k,p=tot;return ;} //注意 p 是引用,其父节点的 lc 或 rc 值会被同时更新 if(val[p]==k) return ; if(k<val[p]) insert(lc[p],k); else insert(rc[p],k); }
4. BST 求前驱/后继
以“后继”为例。(k) 的后继指在 BST 中关键码大于 (k) 的节点中,关键码最小的节点。
初始化 (ans) 为关键码为 (+infty) 的节点。然后,在 BST 中检索 (k)。每经过一个节点,都尝试更新 (ans)。
-
没有找到 (k)。此时 (k) 的后继就在已经经过的节点中,(ans) 即为所求。
-
找到了节点 (p) 使得 (val(p)=k)。若 (rc(p)) 为空,则 (ans) 即为所求;否则,从 (rc(p)) 出发,一直向左走,就找到了 (k) 的后继。
int getnxt(int k){ int ans=2,p=rt; //val(2)=+∞ while(p){ if(val[p]==k){ if(rc[p]>0){p=rc[p]; while(lc[p]>0) p=lc[p]; ans=p;} break; } if(val[p]>k&&val[p]<val[ans]) ans=p; //尝试更新 ans p=k<val[p]?lc[p]:rc[p]; } return ans; }
5. BST 的节点删除
在 BST 中删除关键码为 (k) 的节点。
首先,在 BST 中搜索 (k),得到节点 (p)。
若 (p) 没有左子树或没有右子树,则直接删除 (p),并令 (p) 的子节点代替 (p) 的位置,与 (p) 的父节点相连。
若 (p) 左右子树都有,则在 BST 中求出 (k) 的后继节点 (next)。因为 (next) 没有左子树(因为 (next) 是从 (p) 的右子节点出发,一直向左走得到的),所以可以直接删除 (next),并令 (next) 的右子树代替 (next) 的位置。最后,再让 (next) 节点代替 (p) 节点,删除 (p) 即可。举个栗子:
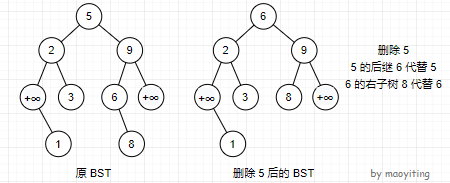
应该还是比较好理解哒,具体见代码。
void del(int &p,int k){ //从子树 p 中删除值为 k 的阶段 if(!p) return ; if(val[p]==k){ //已经检索到值为 k 的阶段 if(!lc[p]) p=rc[p]; //没有左子树,右子树代替 p 的位置,注意 p 是引用 else if(!rc[p]) p=lc[p]; //没有右子树,左子树代替 p 的位置,注意 p 是引用 else{ //既有左子树又有右子树 int nxt=rc[p]; while(lc[nxt]>0) nxt=lc[nxt]; //求后继节点(从 p 的右子节点出发,一直向左走) del(rc[p],val[nxt]); //next 一定没有左子树,直接删除 lc[nxt]=lc[p],rc[nxt]=rc[p],p=nxt; //令节点 next 代替节点 p 的位置。注意 p 是引用 } return ; } if(k<val[p]) del(lc[p],k); else del(rc[p],k); }
三、参考资料
- 《算法竞赛进阶指南》(大棒子,做摘抄 233)
注:这篇文章可能会有锅 QAQ