P5222 Game 题解

题目大意

P5222 Game

一个(N imes M)的棋盘中有(T)个障碍点，棋子不能放在障碍点上，刚开始棋子要放在第一列上，有两种操作

• 将所有棋子都向右移一格，不需要代价

• 将其中一个棋子向上或者向下平移一格，代价是(1)

询问(Q)次，每次询问给出(k_i)的代价，最多可以将多少棋子从第一列移到最后一列

问题求解

从代价去求棋子数很难，我们可以转化一下，已知棋子数求代价，用(ans_i)表示(i)个棋子从第一列移到最后一列的最小代价，最后询问二分求解即可

然后来分析如何求得(ans_i)显然我们可以发现，障碍点的个数比较小，一段没有障碍点的棋盘我们可以将棋子直接移到有障碍点出，所以可以离散化掉，相当于将一段没有棋子的棋盘压缩成一列，将(M)变小，方便于求解，这个是一个非常重要的贪心

现在，(M)的大小已经和(T)同级了，对于每个棋子到底怎么移动我们很难分析，但是可以控制开始棋子数和结束的棋子数，所以考虑用费用流来解决这道题

对于一个不是障碍点的点，对不是障碍点的点建边

• 向右边建一条流量为(1)费用为(0)的点，流量保证了每个点只能放一颗棋子

• 向上下分别建一条流量为(INF)费用为(1)的点，以为上下是可以随便移动的，代价为移动的距离

和很多费用流的题一样，将第一列的所有节点向一个超级原点建边，将最后一列的所有节点向超级汇点建边，流量为(1)费用为(0)，原因同上

我们刷费用流时，每一次增广相当于多放一颗棋子，增广(i)次的代价就是(ans_i)，当这个图不能再增广时说明已经是棋子最多数了

以上就是本篇题解的内容，但是还没有结束

(yzxoi)的题解中提到了一个缩点的想法，将一段没有障碍点的点缩成一个点，将边的数量降到了(NT)，是一个非常非常不错的想法，在随机图上能跑出不错的效果

但是(wpy)苦思冥想了一下午，发现了一种(hack)的情况，如下图

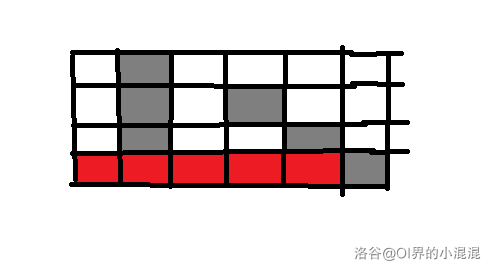
其中黑色的是障碍点，按照缩点算法，我们将红色的点缩成了一个点，所以这个想法在不随机的情况下还是有些问题的，不过能想到还是%%%

代码实现

#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=2e5+5,maxe=4e6+5;
int N,M,K,q,Ans[55],st,st_st,ed,mp[55][4005],lst;
int lnk[maxn],son[maxe],nxt[maxe],w[maxe],c[maxe],cnt=1,Q[maxn];
int dis[maxn],vis[maxn],mincost;
struct AS{
	int x,y;
	bool operator <(const AS B)const {return y<B.y||(y==B.y&&x<B.x);}
}bob[2005];
inline int read(){
	int ret=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
	while(ch<='9'&&ch>='0')ret=ret*10+ch-'0',ch=getchar();
	return ret*f;
}
void add_e(int x,int y,int z,int cost){
	son[++cnt]=y;w[cnt]=z;c[cnt]=cost;nxt[cnt]=lnk[x];lnk[x]=cnt;
}
void add_edge(int x,int y,int z,int cost){
	add_e(x,y,z,cost);add_e(y,x,0,-cost);
}
int calc(int x,int y){
	return M*(x-1)+y;
}
int spfa(){
	int hed=0,til=1;
	memset(dis,INF,sizeof dis);
	memset(vis,0,sizeof vis);
	dis[ed]=0;Q[til]=ed;
	while(hed!=til){
		hed=(hed+1)%maxn;
		int cur=Q[hed];vis[cur]=0;
		for(int j=lnk[cur];j;j=nxt[j]){
			if(w[j^1]>0&&dis[son[j]]>dis[cur]-c[j]){
				dis[son[j]]=dis[cur]-c[j];
				if(!vis[son[j]]){
					vis[son[j]]=1;Q[til=(til+1)%maxn]=son[j];
					int nxt=(hed+1)%maxn;if(dis[Q[til]]<dis[Q[nxt]]) swap(Q[til],Q[nxt]);
				}
			}
		}
	}
	return dis[st]!=INF;
}
int DFS(int x,int delta){
	vis[x]=1;
	if(x==ed||!delta)return delta;
	int flow=0,tmp;
	for(int j=lnk[x];j;j=nxt[j]){
		if(!vis[son[j]]&&w[j]>0&&dis[son[j]]==dis[x]-c[j]&&(tmp=DFS(son[j],min(delta-flow,w[j])))){
			mincost+=(c[j]*tmp);
			w[j]-=tmp;w[j^1]+=tmp;flow+=tmp;
		}
		if(flow==delta)return flow;
	}
	return flow;
}
int Dinic(){
	int maxflow=0;
	if(spfa()){
		int temp=DFS(st,INF);
		maxflow+=temp;
	}
	return maxflow;
}
int main(){
	freopen("lord.in","r",stdin);
	freopen("lord.out","w",stdout);
	N=read();M=read();K=read();q=read();
	for(int i=1;i<=K;i++){bob[i].x=read(),bob[i].y=read();}
	M=1;sort(bob+1,bob+1+K);
	for(int i=1;i<=K;i++){
		if(i!=1&&bob[i].y!=lst){
			if(bob[i].y==lst+1)M++;
			else M+=2;
		}
		lst=bob[i].y;bob[i].y=M;
		mp[bob[i].x][bob[i].y]=1;
	}
	st=N*M+1;ed=st+1;st_st=ed+1;
	for(int i=1;i<=N;i++)if(!mp[i][1]){
		add_edge(st,calc(i,1),1,0);
	}
	for(int i=1;i<=N;i++)
	for(int j=1;j<=M;j++){
		if(mp[i][j])continue;
		if(!mp[i][j+1]&&j<M)add_edge(calc(i,j),calc(i,j+1),1,0);
		if(!mp[i-1][j]&&i>1)add_edge(calc(i,j),calc(i-1,j),INF,1);
		if(!mp[i+1][j]&&i<N)add_edge(calc(i,j),calc(i+1,j),INF,1);
	}
	for(int i=1;i<=N;i++)if(!mp[i][M]){
		add_edge(calc(i,M),ed,1,0);
	}
	for(int i=1;i<=N;i++){
		int ans=Dinic();
		if(ans)Ans[i]=mincost;else N=i-1;
	}
	for(int i=1;i<=q;i++){
		int x=read();
		printf("%d
",upper_bound(Ans+1,Ans+1+N,x)-Ans-1);
	}
	return 0;
}