二叉树
一、树简介
-
树
树是一种借助于复杂节点结构完成的一种数据结构。
树(Tree)是n(n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中:- 有且仅有一个特定的称为根(Root)的结点;
- 当n>1时,其余结点可分为m(m>0)个互不相交的有限集(T_1)、(T_2)、......、(T_n),其中每一个集合本身又是一棵树,并且称为根的子树。
- 此外,树的定义还需要强调:
- n>0时根结点是唯一的,不可能存在多个根结点,数据结构中的树只能有一个根结点。
- m>0时,子树的个数没有限制,但它们一定是互不相交的。
- 节点的度
度就是说明本节点 具有的孩子节点的数目,类似于图算法当中的出度和入度(degree). - 节点关系
父亲节点,孩子节点。 - 树深度
先说明层的概念,从root开始为第一层,依次类推得到深度。
深度为(k)的满二叉树,具有(2^{k+1}-1)个节点,也就是一个简单的等比数列求和,不难理解。
二、二叉树
-
二叉树是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。
-
性质
-
在二叉树的第i层上最多有2i-1 个节点 。(i>=1)
-
二叉树中如果深度为k,那么最多有(2^k-1)个节点。(k>=1)
-
(n_0=n_2+1), (n_0)表示度数为0的节点数,(n_2)表示度数为2的节点数。
-
在完全二叉树中,具有n个节点的完全二叉树的深度为(lfloor {log_2n} floor)+1。
-
若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号,则对完全二叉树中任意一个编号为$ i$ 的结点有如下特性:
(1) 若 i=1,则该结点是二叉树的根,无双亲, 否则,编号为 (lfloorfrac{i}{2} floor)的结点为其双亲结点;
(2) 若 ({2i}gt{n}),则该结点无左孩子, 否则,编号为 2i 的结点为其左孩子结点;
(3) 若({2i+1}gt{n}),则该结点无右孩子结点, 否则,编号为2i+1 的结点为其右孩子结点。
-
-
二叉树的存储结构
-
顺序存储结构
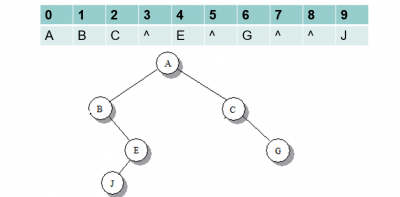
一般情况之下这种存储结构只是简单适用于完全二叉树,在一般情况之下很浪费内存,尤其是右斜树,普适性比较低。
-
链式存储结构
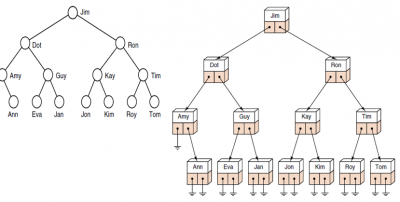
这种结构包括两个左右指针和数据域,声明如下:
typedef struct Node{ ElemType data;//数据 struct Node *lchild, *rchild;//左右孩子指针 } BiTNode, *BiTree;
-
-
二叉树的遍历

-
前序遍历
前序遍历就是从二叉树的根结点
rote出发,当第一次到达结点时就输出结点数据,按照先向左,再向右的方向访问。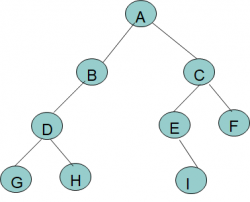
pre-order: A, B, D, G, H, C, E, I, F
-
中序遍历
中序遍历:就是左->中->右。

in-order: G, D, H, B, A, E, I, C, F
-
后序遍历
后序遍历就是左->右->中。

post-order: G, H, D, B, I, E, F, C, A
-
层序遍历(逐层)

-
-
实现代码
由于二叉树借助于递归,代码很简单:
/*二叉树的前序遍历递归算法*/ void PreOrderTraverse(BiTree T) { if(T==NULL) return; printf("%c", T->data); /*显示结点数据,可以更改为其他对结点操作*/ PreOrderTraverse(T->lchild); /*再先序遍历左子树*/ PreOrderTraverse(T->rchild); /*最后先序遍历右子树*/ } /*二叉树的中序遍历递归算法*/ void InOrderTraverse(BiTree T) { if(T==NULL) return; InOrderTraverse(T->lchild); /*中序遍历左子树*/ printf("%c", T->data); /*显示结点数据,可以更改为其他对结点操作*/ InOrderTraverse(T->rchild); /*最后中序遍历右子树*/ } /*二叉树的后序遍历递归算法*/ void PostOrderTraverse(BiTree T) { if(T==NULL) return; PostOrderTraverse(T->lchild); /*先后序遍历左子树*/ PostOrderTraverse(T->rchild); /*再后续遍历右子树*/ printf("%c", T->data); /*显示结点数据,可以更改为其他对结点操作*/ } //完全版本 #include<bits/stdc++.h> using namespace std; const int _max = 3001; typedef struct Node{ int data;//数据 struct Node *lchild, *rchild;//左右孩子指针 }BiTNode, *BiTree; BiTree add(BiTree root, int node) ///插入结点+ { BiTree newnode; BiTree currentnode; BiTree parentnode; newnode = (BiTree)malloc(sizeof(BiTNode)); newnode->data = node; newnode->lchild = NULL; newnode->rchild = NULL; if(root == NULL) ///第一个结点建立 return newnode; else { currentnode = root; ///储存当前结点 while(currentnode != NULL) ///当前结点不为空 { parentnode = currentnode; ///储存父结点 if(currentnode->data > node) currentnode = currentnode->lchild; ///左子树 else currentnode = currentnode->rchild; ///右子树 } if(parentnode->data > node) parentnode->lchild = newnode; else parentnode->rchild = newnode; } return root; } BiTree create(int *data, int len) { BiTree root = NULL; for(int i = 1; i <= len; i++) { root = add(root, data[i]); } return root; } BiTree build_BiTree(int len, int arr[]){ new BiTree[len]; for(int i = 0; i < len; i++){ } } void travel_pre(BiTree T){ if(T==NULL) return; cout<<T->data<<" "; /*显示结点数据,可以更改为其他对结点操作*/ travel_pre(T->lchild); /*再先序遍历左子树*/ travel_pre(T->rchild); /*最后先序遍历右子树*/ } void travel_in(BiTree T){ if(T==NULL) return; travel_in(T->lchild); /*再先序遍历左子树*/ cout<< T->data<<" "; /*显示结点数据,可以更改为其他对结点操作*/ travel_in(T->rchild); /*最后先序遍历右子树*/ } int main() { int num_of_cases; int arr[_max]; while(cin>>num_of_cases && num_of_cases != 0){ for(int i = 1; i <= num_of_cases; i++){ cin >>arr[i]; } BiTree ans = create(arr,num_of_cases); travel_in(ans); cout<<endl; travel_pre(ans); cout<<endl; } }