11月6日NOIP提高组-信心赛总结

分析

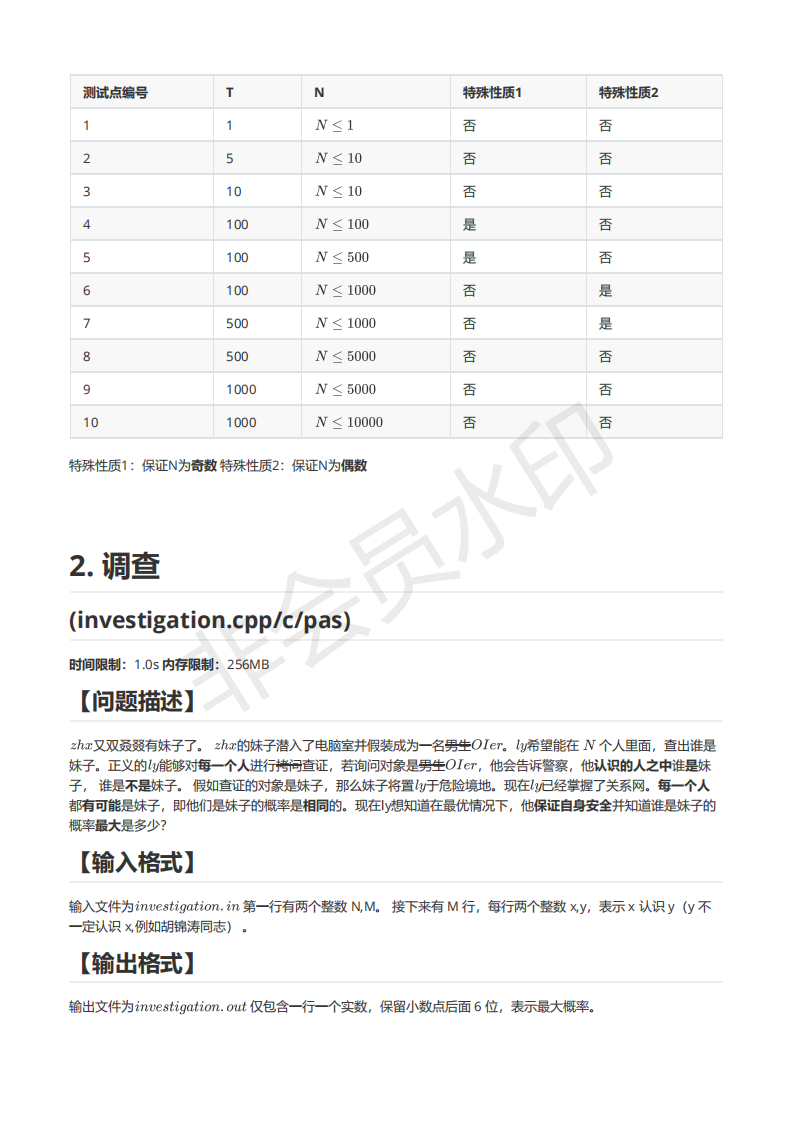
T1：水题，模拟几步策略以后发现就是个骨牌覆盖，奇偶判断走人（我™的把奇偶该输出的输反了爆零）

T2：考场上考虑到可以缩点拓扑序，缩点显然，因为强联通分量里任意一点被确认了整个强联通分量都可以确认，然后入度为0的点最优，但是要特判，就是你其他点都查询过了，剩下一个点，这个点不用查（要满足：这个点所在强联通分量大小为1，找到这个点之前没有一样的点，以及和这个点相连的所有点都可以被其他点所确认（即入度不能为1））

T3：n那么小果断状压（可是并没有写，尝试模拟退火就没时间了）

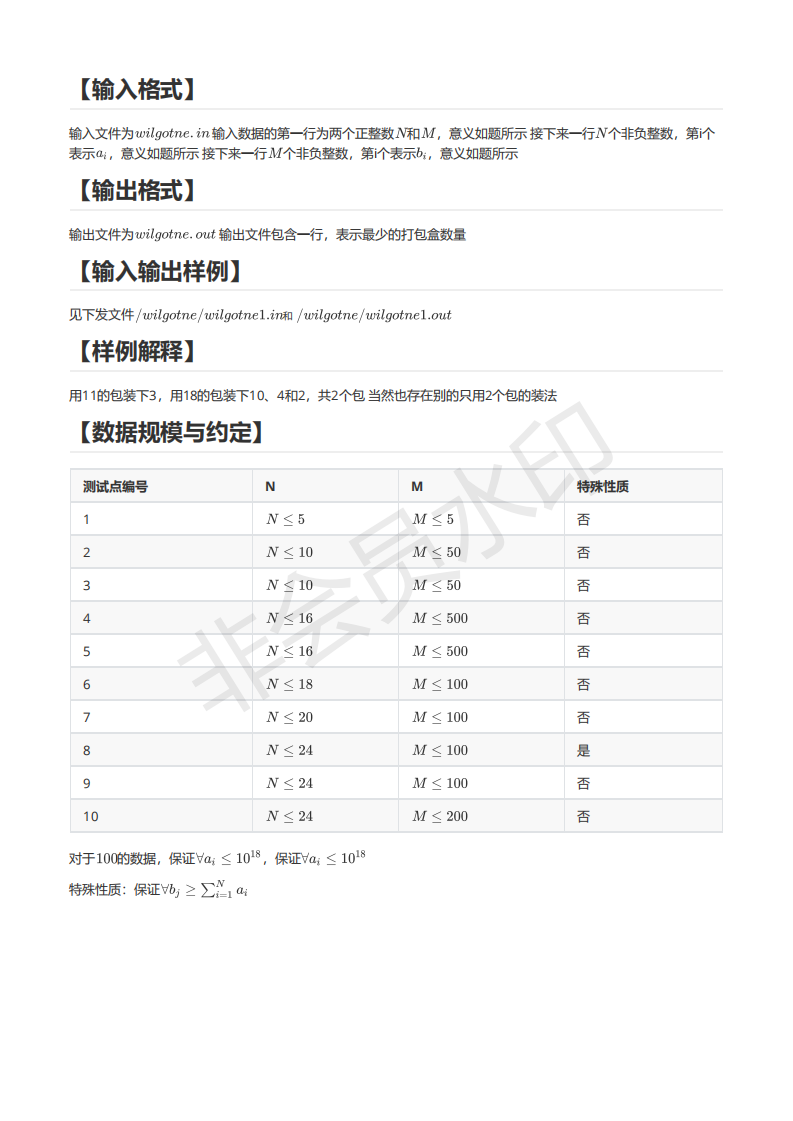
设f[s]为已选物品状态为s的最少饭盒数量，g[s]为已选物品状态为s最少饭盒时，最后那个饭盒还能容纳多少单位的体积

然后可以一个一个的枚举有1的位然后转移，但是这样时间复杂度是O(n*2^n)的，会超时

然后我们发现有1的位就是树状数组的lowbit，用这个求即可，这样时间复杂度就是O(2^n)的了

T1:

#include <iostream>
#include <cstdio>
using namespace std;
int t,n;

int main() {
    freopen("geibei.in","r",stdin);
    freopen("geibei.out","w",stdout);
    scanf("%d",&t);
    while (t--) {
        scanf("%d",&n);
        printf(n%2?"yqw got the geibei!!!
":"hjw got the geibei!!
");
    }
    fclose(stdout);fclose(stdout);
}

T2:

#include <iostream>
#include <cstdio>
using namespace std;
const int N=1e5+10;
const int M=3e5+10;
struct Edge {
    int u,v,nx;
}g[M];
int cnt,list[N];
int bel[N],ind[N],bcnt,sz[N];
int low[N],dfn[N],tme;
int stk[N],top;
bool instk[N],firsttime;
int n,m;

void Add(int u,int v) {
    g[++cnt].u=u;g[cnt].v=v;g[cnt].nx=list[u];list[u]=cnt;
}

void Tarjan(int u,int fa) {
    stk[++top]=u;instk[u]=1;
    low[u]=dfn[u]=++tme;
    for (int i=list[u];i;i=g[i].nx)
        if (!dfn[g[i].v]) {
            Tarjan(g[i].v,u);
            low[u]=min(low[u],low[g[i].v]);
        }
        else
        if (instk[g[i].v]) low[u]=min(low[u],dfn[g[i].v]);
    if (low[u]==dfn[u]) {
        int stktop;
        bcnt++;
        do {
            stktop=stk[top--];instk[stktop]=0;
            bel[stktop]=bcnt;sz[bcnt]++;
        }
        while (stktop!=u);
    }
}

bool Judge(int u) {
    if (firsttime) return 0;
    if (sz[u]!=1) return 0;
    for (int i=list[u];i;i=g[i].nx)
        if (ind[g[i].v]==1) return 0;
    return firsttime=1;
}

int main() {
    freopen("investigation.in","r",stdin);
    freopen("investigation.out","w",stdout);
    scanf("%d%d",&n,&m);
    for (int i=1,u,v;i<=m;i++)
        scanf("%d%d",&u,&v),Add(u,v);
    for (int i=1;i<=n;i++) {
        if (!dfn[i]) Tarjan(i,0);
        list[i]=0;
    }
    cnt=0;
    for (int i=1,fu,fv;i<=m;i++)
        if (bel[g[i].u]!=bel[g[i].v]) {
            Add(bel[g[i].u],bel[g[i].v]);
            ind[bel[g[i].v]]++;
        }
    int ans=0;
    for (int i=1;i<=bcnt;i++)
        if (!ind[i]) {
            if (Judge(i)) continue;
            ans++;
        }
    printf("%.6lf",(double)(n-ans)/n);
    fclose(stdin);fclose(stdout);
}

T3:

#include <iostream>
#include <cstdio>
#include <algorithm>
#define lowbit(x) x&-x
using namespace std;
const int N=1<<24;
const int Inf=2147483647;
int b[510],a[N],f[N],g[N];
int n,m;

bool CMP(int a,int b) {
    return a>b;
}

int main() {
    freopen("wilgotne.in","r",stdin);
    freopen("wilgotne.out","w",stdout);
    scanf("%d%d",&n,&m);
    for (int i=1,a1;i<=n;i++) scanf("%d",&a1),a[1<<i-1]=a1;
    for (int i=1;i<=m;i++) scanf("%d",&b[i]);
    sort(b+1,b+m+1,CMP);
    int mx=(1<<n)-1;
    for (int i=1;i<=mx;i++) {
        f[i]=Inf;
        int j=i;
        do {
            int x=lowbit(j);j-=x;
            if (g[i-x]>=a[x]&&(f[i-x]<f[i]||f[i-x]==f[i]&&g[i-x]-a[x]>g[i])) 
                f[i]=f[i-x],g[i]=g[i-x]-a[x];
            else
            if (b[f[i-x]+1]>=a[x]&&(f[i-x]+1<f[i]||f[i-x]+1==f[i]&&b[f[i-x]+1]-a[x]>g[i]))
                f[i]=f[i-x]+1,g[i]=b[f[i-x]+1]-a[x];
        }
        while (j);
    }
    if (f[mx]>m) {
        printf("-1");
        fclose(stdin);fclose(stdout);
        return 0;
    }
    printf("%d",f[mx]);
    fclose(stdin);fclose(stdout);
}