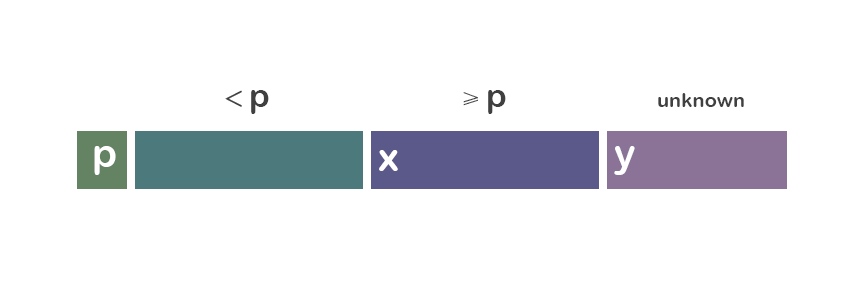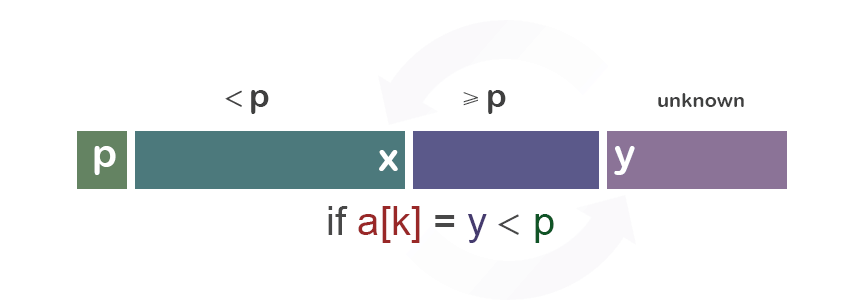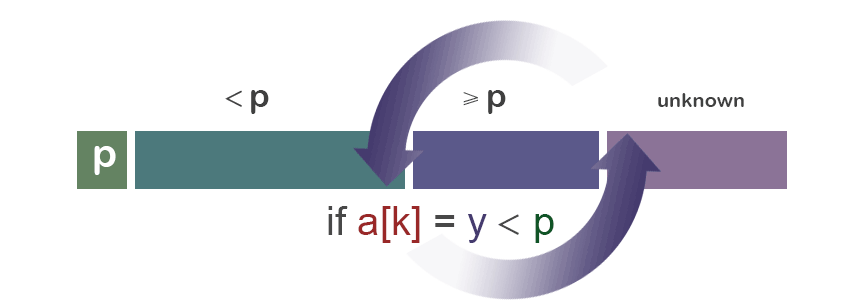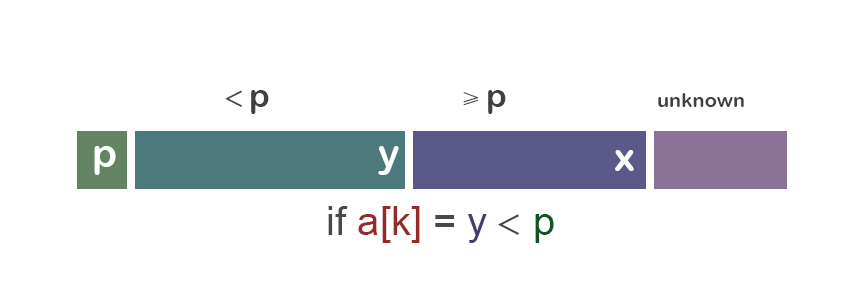数据结构 之 常见的几种“排序”

排序(sorting)是算法家族里比较重要也比较基础的一类，内容也是五花八门了： 1、有“基于比较”的，也有“不基于比较”的； 2、*有迭代的（iterative）也有递归的（recursive）； 3、有利用分治法（divide and conquer）思路解决的；（除了显而易见的“二路归并”算法，*“代入法(substitution method)”也是分治的一种，如快速排序/插入排序）

再进入正文之前，我想推荐大家一个很好的可以可视化学习算法的网站VisuALgo

判断算法的“好坏”，我们一般借助时间（空间）复杂度为依据，包括最好情况/最坏情况/和平均情况的复杂度。

排序方法	平均情况	最好情况	最坏情况	辅助空间	稳定性
冒泡排序	O(n²)	O(n)	O(n²)	O(1)	稳定
简单选择排序	O(n²)	O(n²)	O(n²)	O(1)	不稳定
直接插入排序	O(n²)	O(n)	O(n²)	O(1)	稳定
希尔排序	O(nlogn)~O(n²)	O(nlogn)	O(n²)	O(1)	稳定
堆排序	O(nlogn)	O(nlogn)	O(nlogn)	O(1)	不稳定
归并排序	O(nlogn)	O(nlogn)	O(nlogn)	O(n)	稳定
快速排序	O(nlogn)	O(nlogn)	O(n²)	O(logn)~O(n)	不稳定

1*、迭代的(iterative)与递归的(recursive)的区别 迭代(iterative)指循环反复执行某操作，由旧值递推出新值，每一次对过程的重复称为一次“迭代”，而每一次迭代得到的结果会作为下一次迭代的初始值； 递归(recursive)指程序在运行过程中直接或间接调用自己。递归算法要求有边界条件、递归前段和递归返回段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回。 我们以阶乘(factorial)为例，看看两类算法是如何操作的：

#迭代iterative
def factorial(number):
    product = 1
    for i in range(number):  #主体是循环
        product = product * (i+1)
    return product
m = factorial(5)
print(m)

#递归recursive
def factorial(number):
    if number <= 1:  #递归的边界条件（出口）
        return 1
    else:
        return number * factorial(number-1) #调用自身
n = factorial(5)
print(n)

我们来看一下两个算法运行过程：

对于这个问题来说，迭代比递归的时间效率更高。 不过在真正使用的时候，还需要根据情况讨论两类算法的优劣。

2*、分治法(devide and conquer)中的代入法(substitution method) 分治法，简而言之就是把大问题拆分成小问题，通过递归的求解小问题，最终得到大问题的解。

• 这里插上一小句，分治法与动态规划(Dynamic Programming)看上去很像，都是拆大问题为小问题求解，不过动态规划“更聪明”也更灵活，已求解的子问题会被保存起来，避免重复子问题的反复求解。 另外，动态规划与数学的递归分析法有着很深的渊源，算法的思路往往能够被表示成数组递归的等式。 代入法具体的做法与“数学归纳法”的思路不谋而合： 给出递推过程中第n+1项与第n项的关系； 从第0项开始将每一项的参数带入这个递推公式求解。 重点就在于这个适用于任一个阶段的“递推关系”的确定，这也是神仙算法“快速排序”的精髓。

时间复杂度O(N²)的基于比较的排序算法

通过两两条目进行比较，决定是否将两个条目进行交换（swap）。 这类算法是最容易理解和应用的，但同时并不那么高效，它们的时间复杂度通常为O(N²)。

冒泡排序（Bubble Sort）

算法过程： 1、比较相邻的两个条目（a,b）； 2、如果两个条目的大小关系与排序目标不符，则将两个条目交换；（假设我们想要建立升序序列） 3、重复以上两个步骤直到队尾； 4、这时，队尾条目就为队列中的最大值；这时我们再从步骤1开始重复，交换至倒数第二位；直到队列中所有条目都有序。 时间复杂度： 有内外两个循环，时间复杂度为O(N²)。

改进：提前终止的冒泡排序 如果在内层循环中没有进行交换，那么就意味着该队列已经有序，便可以终止排序操作。 因此对于一个已经有序的序列，其最好情况的时间复杂度为O(n)。 不过这一点改进并不能改变冒泡排序的阶级属性平均时间复杂度。

简单选择排序 （Selection Sort）

算法过程： 1、在[i,N-1]范围内寻找最小的条目的位置X（初始时i=0）； 2、将条目x与条目i交换； 3、将i加1，重复步骤1、2，直到所有条目有序。

void selectionSort(int a[], int N) {
  for (int i = 0; i <= N-2; i++) { 外层循环 O(N)
    int X = min_element(a+i, a+N) - a; //内层循环 O(N)，找到最小条目的位置
    swap(a[X], a[L]); // O(1) 而知也可能相等（并不真正交换）
  }
}

时间复杂度： 同样是内外两层循环，时间复杂度为O(N²)。

插入排序（Insertion Sort）

算法过程： 插入排序的算法思路很像我们在打牌时调整牌序的做法：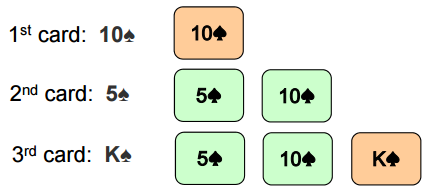

1、开始的时候手里只有一张牌； 2、拿到下一张牌，将牌放到手中牌组的合适位置； 3、每张牌都重复上面的步骤。

void insertionSort(int a[], int N) {
  for (int i = 1; i < N; i++) { // 外层循环 O(N)
    X = a[i]; // X 是将插入的对象
    for (j = i-1; j >= 0 && a[j] > X; j--) //从后往前在已经有序的前i-1个条目中找到应当插入的位置
      a[j+1] = a[j]; // 为X的插入腾出位置
    a[j+1] = X; // 将X插入j+1位
  }
}

时间复杂度： 显然，外层循环的时间复杂度为O(N) 而内层循环的时间复杂度则与待排序序列的有序状况有关：

• 最好情况下，待排序序列已经是有序的，这时候内层循环压根不用找（待排序条目始终比已排序的最后一个条目大）所以这种情况下内层循环的时间复杂度为O(1)；
• 最坏情况下，待排序序列是逆序的，这时候内层每次都要遍历到开头才能找到该插入的位置，这时内层循环的时间复杂度就为O(N)； 综上而言，最好情况下的时间复杂度为O(N)，最坏情况下为O(N²)，平均情况下的时间复杂度为O(N²)。

时间复杂度O(NlogN)的基于比较的排序算法

归并排序（Merge Sort）

算法过程： 1、将两个条目分为一组，合并成为有序的长度为2的序列； 2、将两个已排序的长度为2的序列分为一组，合并成为有序的长度为4的序列； 重复该步骤... 3、最终，将两个已排序的长度为(N/2)的序列合并成为有序的长度为N的序列，排序完成。

以上只是大体的思路，去进一步了解归并排序，我们先从“合并”(merge)这个操作谈起： 从两个待合并序列的首部开始，边比较边向后移（取出两边指针所指的较小条目的到辅助队列中去，并将指针向后移一位）

void merge(int a[], int low, int mid, int high) {
  // 子序列1 = a[low..mid], 子序列2 = a[mid+1..high], 都是有序的
  int N = high-low+1;
  int b[N]; // 一个辅助数组
  int left = low, right = mid+1, bIdx = 0; //初始化子序列和辅助序列的指针
  while (left <= mid && right <= high) // 合并过程
    b[bIdx++] = (a[left] <= a[right]) ? a[left++] : a[right++];
  while (left <= mid) b[bIdx++] = a[left++]; // 处理余下的部分
  while (right <= high) b[bIdx++] = a[right++]; //  处理余下的部分
  for (int k = 0; k < N; k++) a[low+k] = b[k]; // 将辅助数组中的内容粘贴回去
}

以上就是归并排序算法的灵魂核心所在了。 还记得之前提到过的“分治法”（Divide and Conquer）吗？ 将大问题拆分正小问题，通过解决小问题递归的解决大问题。

归并排序就是一个典型的利用“分治法”思路的算法： “分”的过程很容易：将待排序的序列一分为二，一直分到不能再分（单个条目），再通过迭代的思路回溯着求解； “治”的部分就是我们刚刚介绍的合并（merge）的过程。

完整算法过程:

void mergeSort(int a[], int low, int high) {
  // 待排序的序列是a[low..high]
  if (low < high) { // 迭代的出口是单个条目或空（low>=high）
    int mid = (low+high) / 2;   
    mergeSort(a, low  , mid ); // 将序列一分为二，迭代求解（recursive）
    mergeSort(a, mid+1, high); 
    merge(a, low, mid, high); // “治”的部分，合并子序列
  }
}

时间复杂度：

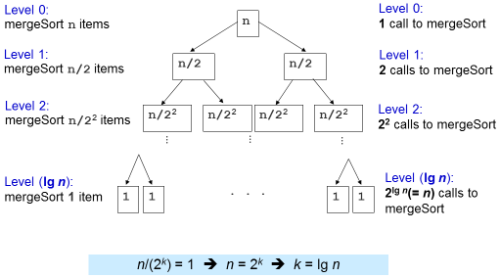
对于每一次长度为k的序列的合并（merge）操作来说，它的时间复杂度是O(k)。（最多有k-1次比较，当两个待合并的序列正好“镶嵌”时） 由上图可知，在第k层，每一个待合并的序列长度为n/(2^(k-1))，需要执行合并的次数为2^(k-1)。 所以可以得到，在第k层，合并的总的时间复杂度为O[N/(2^(k-1))]*O[2^(k-1)] = O(N)； 易知该归并树一共有logN层，所以可得归并排序总的时间复杂度为O(NlogN)。

归并排序的一个很大优点就是，无论待排序的序列情况如何，其时间复杂度都是O(NlogN)。 这种性质使得其适用于大规模的排序。（NlogN的增长速度远小于N²）

不过，归并排序也有一些弱势的部分： 1、算法稍显复杂；（不过我们也不需要从底层写起(from scratch)） 2、需要O(N)的空间复杂度（一个辅助队列），使得这个算法不是就地算法。

快速排序（Quick Sort）

快速排序也是一个使用“分治法”思路的算法。 算法过程： 我们用“分治法”的思路来分析算法： “分”的部分： 选择一个条目p（相当于一个中央标杆） 然后将待排序序列a[i...j]分为三部分：a[i...m-1],a[m],a[m+1...j]

• a[i...m-1]（可能为空）中的条目都小于刚才选定的标杆a[p]的值；
• a[m]的值为标杆的值（可以认为这里是把标杆a[p]移动到了排序后正确的位置上）
• a[m+1...j]（可能为空）中的条目都大于标杆的值。 接下来，将该过程应用在左右这两个子序列中，迭代下去。

“治”的部分： ...什么都不做。

是不是感觉和之前讨论的“归并排序”完全相反呢？

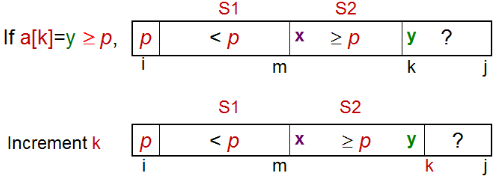
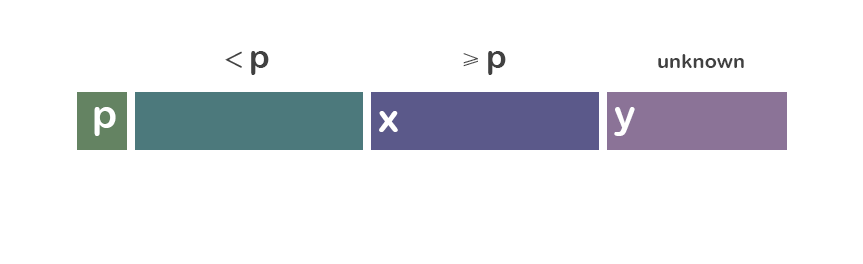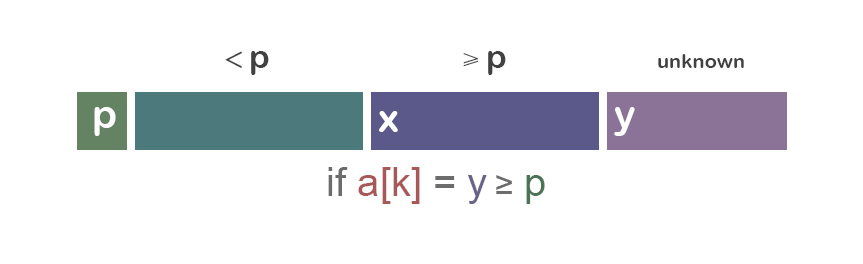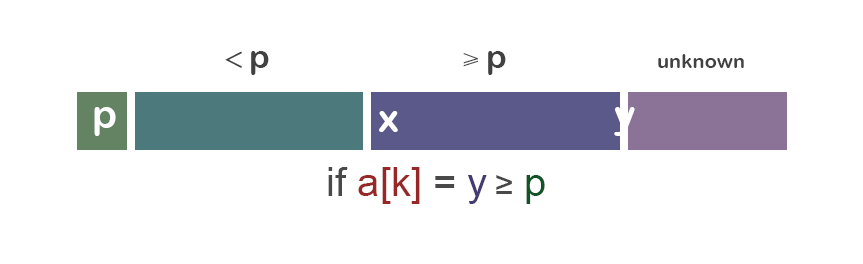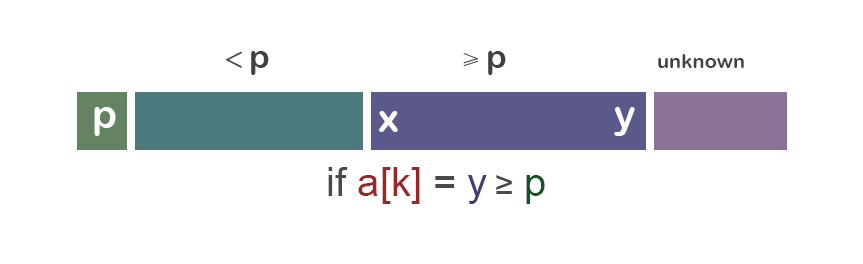
我们先从重要的“分”的部分（经典版本）开始讨论： 为了分隔a[i...j]，我们先选择a[i]作为中央标杆p。 余下的元素被分到到三个区域： ① S1 = a[i+1...m] 其中元素都 ＜ p； ② S2 = a[m+1...k-1] 其中元素 ≥ p； ③ 未知区域 = a[k...j] 尚未分配至S1/S2。

初始时，S1区和S2区都是空的；即除了p自身，所有的元素都在“未知区域”中。 对于每一个在未知区域中的元素a[k]，我们将其与p比较，决定其分到S1还是S2。

先通过图片来对“分组”的操作有一个直观的认识：

情况一：a[i] ≥ p

情况二：a[i] ＜ p

算法实现:

int partition(int a[], int i, int j) {
  int p = a[i]; // 选择a[i]作为中心轴
  int m = i; // S1和S2初始情况下都是空的
  for (int k = i+1; k <= j; k++) { // 遍历未知区域
    if (a[k] < p) { // 情况2
      m++;
      swap(a[k], a[m]);
    } // 对于情况1： a[k] >= p，仅仅k++，无额外操作
  }
  swap(a[i], a[m]); // 最后一步，将a[m]与a[i]交换，将中心轴放在最终位置
  return m; // 返回p最终位置的下标
}

void quickSort(int a[], int low, int high) {
  if (low < high) {
    int m = partition(a, low, high); // 时间复杂度 O(N)
    // m为low最终的位置
    quickSort(a, low, m-1); // 迭代求解左边分组
    quickSort(a, m+1, high); // 迭代求解右边分组
  }
}

复杂度分析： 首先，分析每一次“分组”(partition)的复杂度： 对于partition(a,i,j),只需要递归执行(j-i)次（将未分组的条目一一分组），所以它的时间复杂度是O(N)。

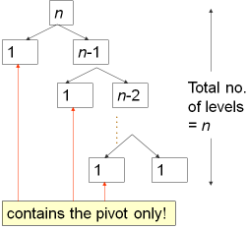
最坏的情况下，即如果序列本来就是有序的，那么每次都选择第一个条目作为“中心轴”的结果就是，分组的左半边只有p(x≤p)，而余下的条目都在右半边（x＞p）。 这种情况下一共需要执行n-1次“分组”的操作。总的时间复杂度为O(N²)。

而最好的情况下，每一次选择的p都能够将序列分为相等大小的两部分。 这种情况下，递归的深度只有O(logN)（与归并排序相类似），每一层的时间复杂度为O(N)，得到总的时间复杂度为O(NlogN)。

随机快速排序（Random Quick Sort）

随机快速排序与快速排序不同的一点就是，相对于从“固定”的位置选择p（比如一直选择起始部分的元素作为p），p的选择是随机的。

为什么这个随机快速排序的时间复杂度为O(NlogN)呢？解释起来可能稍显繁琐，不过我们可以建立一种直观的感受： 如果是随机选择p的话，我们遇到极端情况的概率（完全正序）就会很小，（可以把它想象成符合一种温和的正态式的随机分布）那么这种“较好情况”和“较差情况”碰撞叠加相平均，结果便会得到O(NlogN)的时间复杂度。

不基于比较的排序算法

基于比较的排序算法时间复杂度的下限为O(NlogN)，也就是说，能够做到最坏情况的时间复杂度也为O(NlogN)的算法就可以被视作最优算法了。

然而，如果使用不基于比较的排序方法，我们可以“变得更快”，甚至达到O(N)的时间复杂度。(不过待排序列需要满足一些前提条件)

计数排序（Counting Sort）

前提条件：如果待排序的序列为小范围内的整型数(Integer)，我们只需记下每个整型数出现的频次，再按序输出就行了。

例如，待排序序列的范围是[1,9]，只需要记录下“1”出现了多少次，“2”出现了多少次……再按从1到9的顺序输出就行了。

基数排序（Radix Sort）

前提条件：待排序的序列可以是较大范围的整型数，但是位数不能太大。

基数排序又被称为“桶子法”（Bucket Sort）。在基数排序中，我们将每个待排序的数视作一个 w 长的字符串（如果长度不够可以在前面添零）

① 先从最右位（最小位）开始，将待排序的数根据最小位的数值分到（0~9）这十个“桶子”中去，再从“0号桶”开始，依次将每个桶子中的数取出来，排成一个最小位有序的序列。 ② 接着，根据倒数第二位的数值，“依序”将各数再次分到十个“桶子”中去，然后将每个桶子中的数取出排列成新的序列。（注意取出的时候要维持放入桶中的顺序）这个时候得到就是后两位有序的序列了。 ③ 重复这个操作，直到最左位，便可得到有序的数列了。

不难看出，这个排序方法是“稳定”的。其时间复杂度为O(w*(N+k))

“放”的时间复杂度为O(N)，“取”的时间复杂度为O(k)(这里指有k个“桶”)，一共需要操作w次（共有w位）。

堆排序（Heap Sort）

背景知识 堆有以下两个性质：

• 是一棵完全二叉树（就是只有最下一层的右侧可为空的满二叉树）
• 堆中某个节点的值总是不大于（大根堆）或不小于（小根堆）其父节点的值

一个完全二叉树能够被存储成为一个数列A（从根节点开始，层序遍历入队），由此一来，我们能够很容易得到节点之间的关系： 1、父节点 parent(i) = i>>1 (1/2) 2、左子节点 left(i) = i<<1 (i2) 3、右子节点 right(i) = i<<1 + 1 (i2+1)

一般步骤

1、初始建成一个大根堆； 2、将堆顶元素取出，并将堆末尾（对应的数列的末尾元素）移至堆顶处； 3、调整堆中的元素位置，再次构成大根堆，回到第一步，直到所有元素被取出。

添加元素 insert(v)

为了保证堆的完全二叉树的特性，添加元素只能在末尾添加。 添加元素之后，可能会破坏堆的顺序，因此要进行相应的交换调整。 时间复杂度为O(logN)

初始化堆 heapify()

有两种时间复杂度不同的初始方式：

• siftUp： O(NlogN)初始为空，每在末尾添加一个元素，都要进行交换排序；
• siftDown：O(N)初始是一个没有经过排序的二叉树，在其基础上进行排序调整；

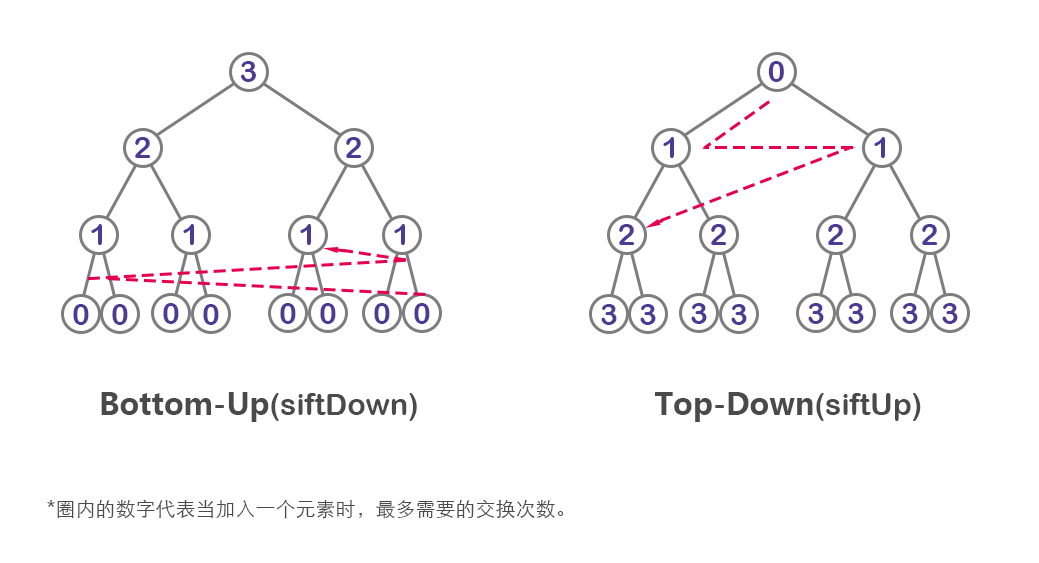
从直观上看一下这两种初始化方式的时间复杂度区别:

• siftUp的每添加一个元素，相当于在当时的高度h上进行了一次顺序调整；然而这个高度h随着元素的添加在不断升高，高度越高，调用“调整”的次数就越多，“调整”的时间复杂度近似向最末层的时间复杂度O(logN)靠拢，故总的时间复杂度为O(NlogN)；
• 而siftDown与之相反，需要“调整”的次数由下层至上层递增，“调整”的时间复杂度像下靠拢（O(1)），得到总的时间复杂度为O(N)。

调整 siftDown()

在元素数为K时，可得其调整的时间复杂度为O(h) = O(logK) 因为底层的元素较多，所以我们可以认为整体的时间复杂度向下靠拢(O(logN)) 因此可以得到堆排序的总的时间复杂度为O(N)[初始堆]+O(NlogN)[调整] = O(NlogN)