关于树的基本定义可以百度,简单说一下“树"的特点:
1)每个节点有0个或者多个子节点
2)没有父节点的节点称为根节点
3)每一个非根节点有且只有一个父节点
4)除了根节点外,每一个子节点可以分为多个不相交的子树
树的术语
1)节点的度:一个节点含有子树的个数
2)树的度:一棵树,最大的节点的度
3)叶节点或终端节点:度为0的节点
。。。。百度一下,基本都是顾名思义
树的种类(具体百度)
1)无序树
2)有序树
1)二叉树
1.完全二叉树:除了叶节点那层,上面所有层的每一个节点达到最大数。(满二叉树)
2.平衡二叉树
3.排序二叉树
2)霍夫曼数
3)B树
树虽然也可以顺序存储,但是不方便,一半都是链式存储。
树的建立,添加与遍历
#!/usr/bin/env python #-*-coding:utf-8 -*- class Node(object): # 二叉树节点 def __init__(self,item): self.elem = item self.lchild = None self.rchild = None class Tree(object): """二叉树""" def __init__(self): self.root = None def add(self,item): """以层次遍历的方式添加元素""" # 先构造一个节点 node = Node(item) if self.root is None: self.root = node return # 建立一个队列,遍历一下,看在哪添加 queue = [self.root] while queue: cur_root = queue.pop(0) if cur_root.lchild is None: cur_root.lchild = node return else: queue.append(cur_root.lchild) if cur_root.rchild is None: cur_root.rchild = node return else: queue.append(cur_root.rchild) def breadth_travel(self): """广度遍历(层次遍历)""" if self.root is None: return queue = [self.root] while queue: cur_node = queue.pop(0) print(cur_node.elem, end=" ") if cur_node.lchild is not None: queue.append(cur_node.lchild) if cur_node.rchild is not None: queue.append((cur_node.rchild)) """下面是树的深度遍历,深度遍历有三种: 先序遍历,先输根,后左子树右子树; 中序遍历,先左,然后跟,最后右; 后序遍历,先左右,后根""" def preorder(self,node): # 先序遍历 if node is None: return print(node.elem,end=" ") self.preorder(node.lchild) self.preorder(node.rchild) def inorder(self,node): # 中序遍历 if node is None: return self.inorder(node.lchild) print(node.elem,end=" ") self.inorder(node.rchild) def postorder(self,node): # 后序遍历 if node is None: return self.postorder(node.lchild) self.postorder(node.rchild) print(node.elem, end=" ") if __name__ == '__main__': # 构造一个树 tree = Tree() # 添加元素 tree.add(1) tree.add(2) tree.add(3) tree.add(4) tree.add(5) tree.add(6) tree.add(7) tree.add(8) tree.add(9) # 层次遍历 tree.breadth_travel() print("") # 先序遍历 tree.preorder(tree.root) print("") # 中序遍历 tree.inorder(tree.root) print("") # 后序遍历 tree.postorder(tree.root)
输出:
1 2 3 4 5 6 7 8 9
1 2 4 8 9 5 3 6 7
8 4 9 2 5 1 6 3 7
8 9 4 5 2 6 7 3 1
上面代码通过添加元素建立的树,样式可看https://www.cnblogs.com/maxiaonong/p/10060086.html
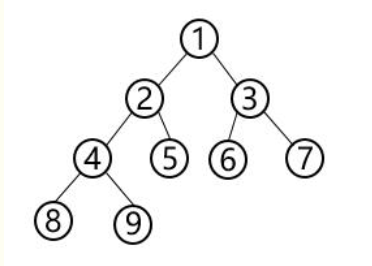
如何由先序,中序,后序倒推树的结构尼?其实只要知道中序,再任意知道一个(先序与后序中一个)就可以倒推出来。不过不能只知道先后序,这样不行,因为中序根把左右分开,没有中序,只有先后,左右分不开。
假设给了先序遍历的结果:1 2 4 8 9 5 3 6 7,中序遍历的结果8 4 9 2 5 1 6 3 7;
分析:先序特点:根-左-右,中序:左-根-右;看先序第一个1,肯定是老根,因此8 4 9 2 5 1 6 3 7;
接着根据左右个数先序左右也分开了:1 2 4 8 9 5 3 6 7
同理:第二层左根为2,那中序得:8 4 9 2 5,那先序2 4 8 9 5
以此往下。可以倒推出上面树的模型,然后可以再后序遍历。
关于二叉树的常见问题:
问题一:树的递归和非递归遍历

#!/usr/bin/env python #-*-coding:utf-8 -*- class Node(object): def __init__(self,value=None,left=None,right=None): self.value = value self.right = right self.left = left """二叉树的递归遍历""" def pre_travel(root): # 前序遍历 if not root: return print(root.value,end=' ') pre_travel(root.left) pre_travel(root.right) def mid_travel(root): # 中序遍历 if not root: return mid_travel(root.left) print(root.value,end=' ') mid_travel(root.right) def after_travel(root): # 后序遍历 if not root: return after_travel(root.left) after_travel(root.right) print(root.value, end=' ') """非递归遍历""" def non_pre_travel(root): # 非递归前序遍历 if not root: return stack=[] # 借助堆栈 while stack or root: if root: stack.append(root) print(root.value,end=' ') root = root.left else: # 进入else说明左子树到头了 root = stack.pop() # 依次弹出左子树,第一次弹出的是没右,循环进入else接着弹 root = root.right def non_mid_travel(root): # 非递归中序遍历 if not root: return stack = [] while stack or root: if root: stack.append(root) root = root.left else: root = stack.pop() print(root.value,end=' ') root = root.right def non_after_travel(root): # 非递归后序遍历,因为先左后右最后中,跳跃性导致有点难度; # 这里按照中、右子树、左子树的顺序存在堆栈2中,再依次弹出。 if not root: return # 要用两个堆栈 stack1 = [] stack2 = [] node = root stack1.append(node) while stack1: # 这个while循环用户找到后续遍历的逆序,存在stack2中 node = stack1.pop() if node.left: stack1.append(node.left) if node.right: stack1.append(node.right) stack2.append(node) while stack2: print(stack2.pop().value,end=' ') if __name__ == '__main__': # 建立上图所示的二叉树 root = Node(1,Node(2,Node(4,Node(8),Node(9)),Node(5)),Node(3,Node(6),Node(7))) print("-------------------------递归解法---------------------------:") print("前序递归遍历结果如下:") pre_travel(root) print("") print("中序递归遍历结果如下:") mid_travel(root) print("") print("后序递归遍历结果如下:") after_travel(root) print("") print("-----------------------非递归解法---------------------------:") print("非递归前序遍历结果:") non_pre_travel(root) print("") print("非递归中序递归遍历结果如下:") non_mid_travel(root) print("") print("非递归后序递归遍历结果如下:") non_after_travel(root)
问题二:二叉树广度优先遍历(层次遍历),上有略。
问题三:求二叉树的深度

"""求二叉树的深度""" # 非递归法 def non_depth(root): if not root: return 0 queue = [root] depth = 0 # 注意这里初始是0,原因在于last last = queue[-1] while queue: node = queue.pop(0) if node.left: queue.append(node.left) if node.right: queue.append(node.right) if last==node: depth += 1 # 更新last if queue: last = queue[-1] return depth # 递归法求二叉树的深度 def depth(root): if not root: return 0 left = depth(root.left) right = depth(root.right) return max(left+1,right+1) if __name__ == '__main__': # 建立上图所示的二叉树 root = Node(1,Node(2,Node(4,Node(8),Node(9)),Node(5)),Node(3,Node(6),Node(7))) print("二叉树的深度是(非递归法):",non_depth(root)) print("二叉树的深度是(递归法):",depth(root))
问题四:已知前序与中序求后序遍历结果

##一直二叉树前序遍历和中序遍历,求后序遍历 def find_tree(preList, midList, afterList): """这里的参数是列表类型,afterList为空列表,原地改""" if len(preList) == 0: return if len(preList) == 1: afterList.append(preList[0]) return root = preList[0] n = midList.index(root) find_tree(preList[1:n + 1], midList[:n], afterList) find_tree(preList[n + 1:], midList[n + 1:], afterList) afterList.append(root) if __name__ == '__main__': preList = ['1','2','4','8','9','5','3','6','7'] midList = "849251637" afterList = [] find_tree(preList,midList,afterList) print(afterList)
问题四:二叉树中两节点的最低公共祖先
题目letcode上也有,注意还有一个二叉搜索树的最低公共祖先,二叉搜索树有一个特性就是左子树都小于父亲节点,右子树都大于父亲节点。所以二叉搜索树简单一点。
下面是问题四的解:

"""求二叉树两个节点的最低公共祖先 思路: 递归,如果当前节点就是p或q,说明当前节点就是最近的祖先, 如果当前节点不是p或p,就试着从左右子树里找pq。 如果pq分别在一左一右被找到,那么当前节点还是最近的祖先返回root就好了, 否则,返回它们都在的那一边。""" def lowestCommonAncestor(root, p, q): """ :type root: TreeNode :type p: TreeNode :type q: TreeNode :rtype: TreeNode """ if not root or root == p or root == q: return root else: left = lowestCommonAncestor(root.left, p, q) right = lowestCommonAncestor(root.right, p, q) if left and right: # 一个在左子树,一个在右子树 return root elif left: # 都在左子树 return left elif right: # 都在右子树 return right else: return if __name__ == '__main__': # 建立上图所示的二叉树 root = Node(1,Node(2,Node(4,Node(8),Node(9)),Node(5)),Node(3,Node(6),Node(7))) p = root.right.right # 假设一个节点是7 q = root.left # 一个节点是2 re = lowestCommonAncestor(root,p,q) print(re.value)

#!/usr/bin/env python #-*-coding:utf-8 -*- class Node(object): # 二叉树节点 def __init__(self,item): self.elem = item self.lchild = None self.rchild = None class Tree(object): """二叉树""" def __init__(self): self.root = None def add(self,item): """以层次遍历的方式添加元素""" # 先构造一个节点 node = Node(item) if self.root is None: self.root = node return # 建立一个队列,遍历一下,看在哪添加 queue = [self.root] while queue: cur_root = queue.pop(0) if cur_root.lchild is None: cur_root.lchild = node return else: queue.append(cur_root.lchild) if cur_root.rchild is None: cur_root.rchild = node return else: queue.append(cur_root.rchild) def breadth_travel(self): """广度遍历(层次遍历)""" if self.root is None: return queue = [self.root] while queue: cur_node = queue.pop(0) print(cur_node.elem, end=" ") if cur_node.lchild is not None: queue.append(cur_node.lchild) if cur_node.rchild is not None: queue.append((cur_node.rchild)) """下面是树的深度遍历,深度遍历有三种: 先序遍历,先输根,后左子树右子树; 中序遍历,先左,然后跟,最后右; 后序遍历,先左右,后根""" def preorder(self,node): # 先序遍历 if node is None: return print(node.elem,end=" ") self.preorder(node.lchild) self.preorder(node.rchild) def inorder(self,node): # 中序遍历 if node is None: return self.inorder(node.lchild) print(node.elem,end=" ") self.inorder(node.rchild) def postorder(self,node): # 后序遍历 if node is None: return self.postorder(node.lchild) self.postorder(node.rchild) print(node.elem, end=" ") # 返回二维列表,内部每个列表表示找到的路径 def FindPath(self, root, expectNumber): if not root: return [] if not root.lchild and not root.rchild and root.elem == expectNumber: return [[root.elem]] tmp = [] left = self.FindPath(root.lchild,expectNumber-root.elem) right = self.FindPath(root.rchild,expectNumber-root.elem) for item in left+right: tmp.append([root.elem]+item) return tmp if __name__ == '__main__': # 构造一个树 tree = Tree() # 添加元素 tree.add(10) tree.add(5) tree.add(12) tree.add(4) tree.add(7) # # 层次遍历 # tree.breadth_travel() # print("") # 先序遍历 tree.preorder(tree.root) print("") # # 中序遍历 # tree.inorder(tree.root) # print("") # # 后序遍历 # tree.postorder(tree.root) print(tree.FindPath(tree.root,22))

