一 邻近算法的基本介绍
1 基本说明
邻近算法又叫做K临近算法或者KNN(K-NearestNeighbor),是机器学习中非常重要的一个算法,but它简单得一塌糊涂,其核心思想就是样本的类别由距离其最近的K个邻居投票来决定。现在假设我们已经有一个已经标记好的数据集,也就是说我们已经知道了数据集中每个样本所属于的类别。这个时候我们拥有一个未标记的数据样本,我们的任务是预测出来这个数据样本所属于的类别。显然邻近算法是属于监督学习(Supervised Learning)的一种,它的原理是计算这个待标记的数据样本和数据集中每个样本的距离,取其距离最近的k个样本,那么待标记的数据样本所属于的类别,就由这距离最近的k个样本投票产生。在这个过程中,有一个动作是标记数据集,这一点在企业中一般是有专门人来负责标记数据的。
2 举例说明
为了更加直观的了解邻近算法,请看下面的例子。有两种水果长得非常像,一个是菠萝,另一个是凤梨,很长一段时间我都以为它们是同一种水果。
菠萝与凤梨的核心区别是菠萝的叶子有刺,而凤梨的叶子没有刺。菠萝的凹槽处的颜色是黄色,而凤梨的凹槽处的颜色是绿色。首先我们把这两种水果抽取出其中的两个特点(凹槽处的颜色、叶子上是否有刺)后,放入一个直角坐标系中吧。如下图: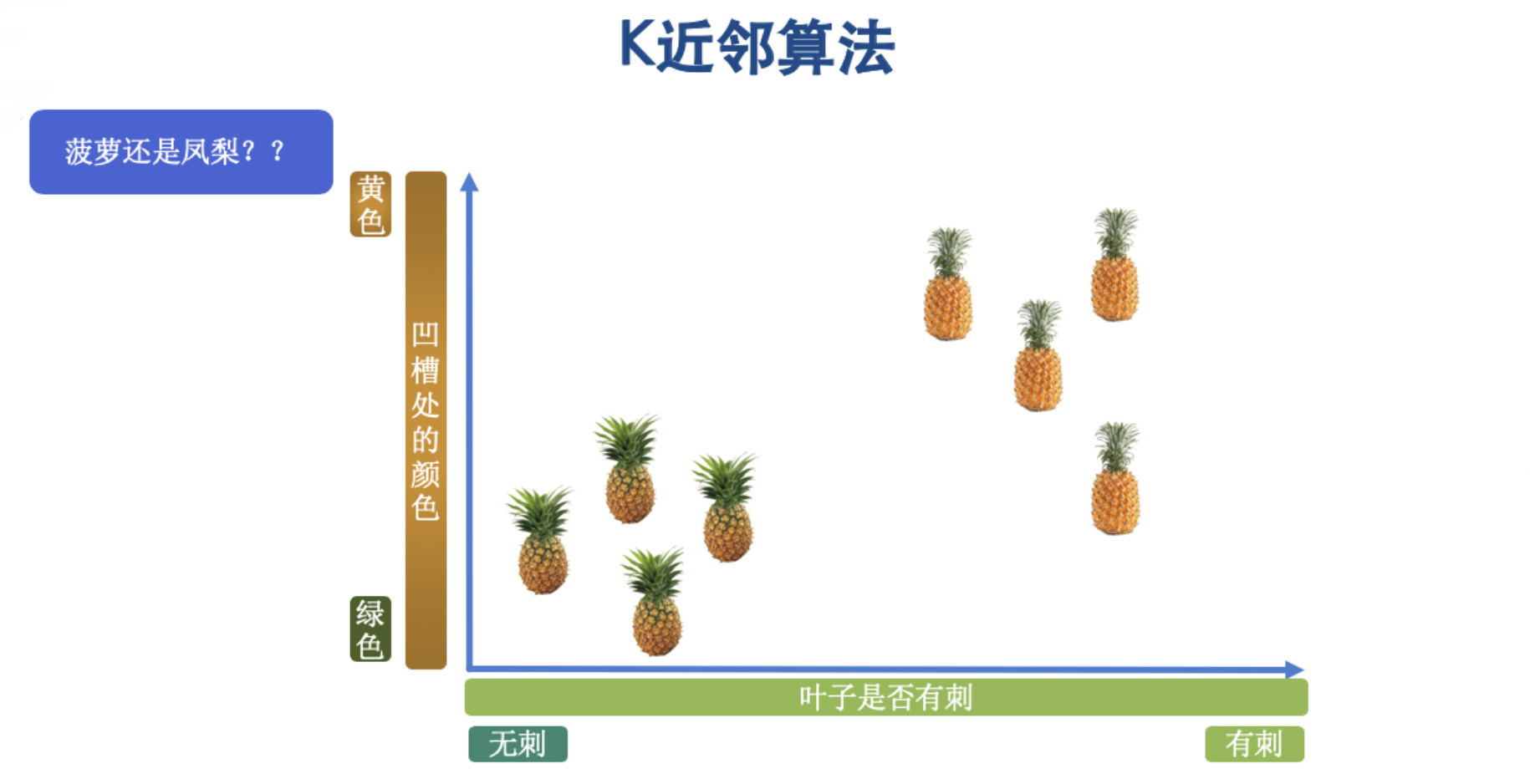
我们按照两种水果的特点,已经把它们放在了直角坐标系中,按照我们所说的算法原理,此时有一个未标记的样本,我们来预测这个样本到底是属于哪种水果。如下图,这个时候来了一个未标记的样本,也就是不知道是什么类别的水果。
在原理中,我们说过,由其最近的K个邻居来投票决定,这个未标记的水果到底是什么水果,那么这个时候,我们把K的值设置为3,如下图: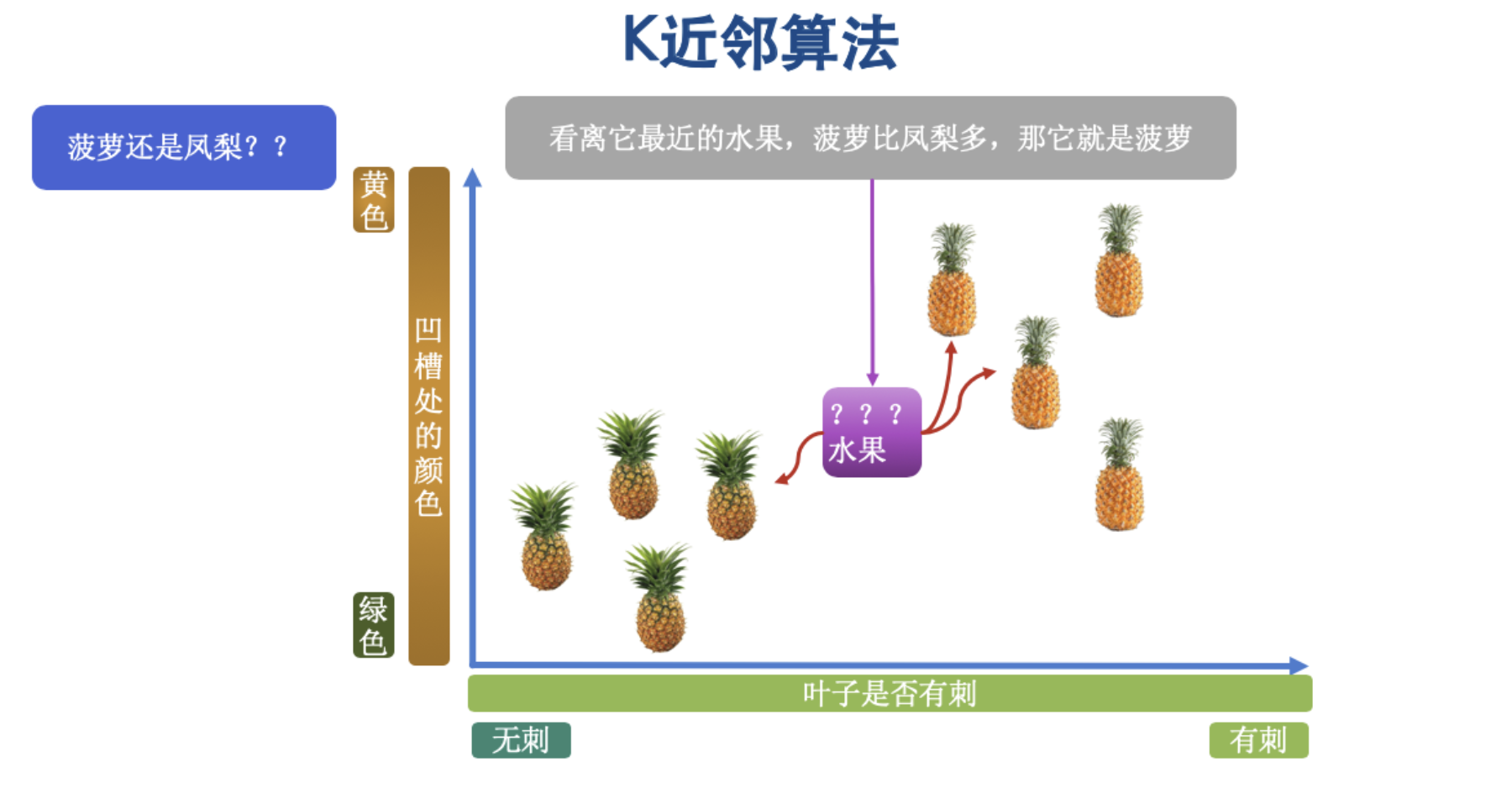
从图片中,我们看到,在K的值为3的时候,与未标记样本最近的3个邻居其中2个为菠萝,而1个为凤梨,那么这个时候我们预测这个未知的水果为菠萝。
3 伪代码说明
我们先来看一下如何用伪代码来实现这个算法,这样我们在后边的学习中才能更好的写出来这段代码。
- 第一步,我们设x_test为待标记的数据样本,x_train为已标记的数据集。
- 第二步,遍历x_train中的所有样本,计算每个样本与x_test的距离,并把距离保存在distance数组中。
- 第三步,对distance数组进行排序,取距离最近的k个点,标记为x_knn。
- 第四步,在x_knn中统计每个类别的个数,即class0(类别0)在x_knn中有几个样本,class1 (类别1)在x_knn中有几个样本。
- 第五步,待标记样本的类别,就是x_knn中样本个数最多的那个类别。
4 优缺点分析
- 优点:准确性高,对异常值有较高的容忍度,原因是异常值会单独分布在坐标系的一个角落,取k个邻居的时候大概率失去不到这个异常值的。
- 缺点:计算量大,对内存的需求也大,因为它每次对一个未标记的样本进行分类的时候,都需要全部计算一下距离。
- 关键点:k值的选取,首先k值一定是奇数,这样可以确保两个类别的投票不会一样,其次,k值越大,模型的偏差越大,对于噪声数据(错误数据或异常数据)越不敏感,k值太小就会造成模型的过拟合。
二 邻近算法的代码练习
1 准备数据
# 从sklearn库中的数据集对象里导入样本生成器中的make_blobs方法帮助我们生成数据
from sklearn.datasets.samples_generator import make_blobs
# 声明三个直角坐标系中的位置
centers = [[-2, 2], [2, 2], [0, 4]]
# 生成数据,其中n_samples是生成数据的个数,centers是中心点,cluster_std是标准差,指明离散程度
x, y = make_blobs(n_samples=60, centers=centers, cluster_std=0.6)
# x是生成的数据,y是不同的数据对应所属的的类别0,1,2
print(x, y)
2 用图形来帮助理解
import matplotlib.pyplot as plt
import numpy as np
plt.figure(figsize=(16, 10), dpi=144)
c = np.array(centers)
# x轴,y轴,c颜色 s指定点的大小
plt.scatter(x[:, 0], x[:, 1], c=y, s=100, cmap="cool")
# 画出中心点
plt.scatter(c[:, 0], c[:, 1], s=100, marker="^", c="orange")
plt.show()
图形显示如下图所示: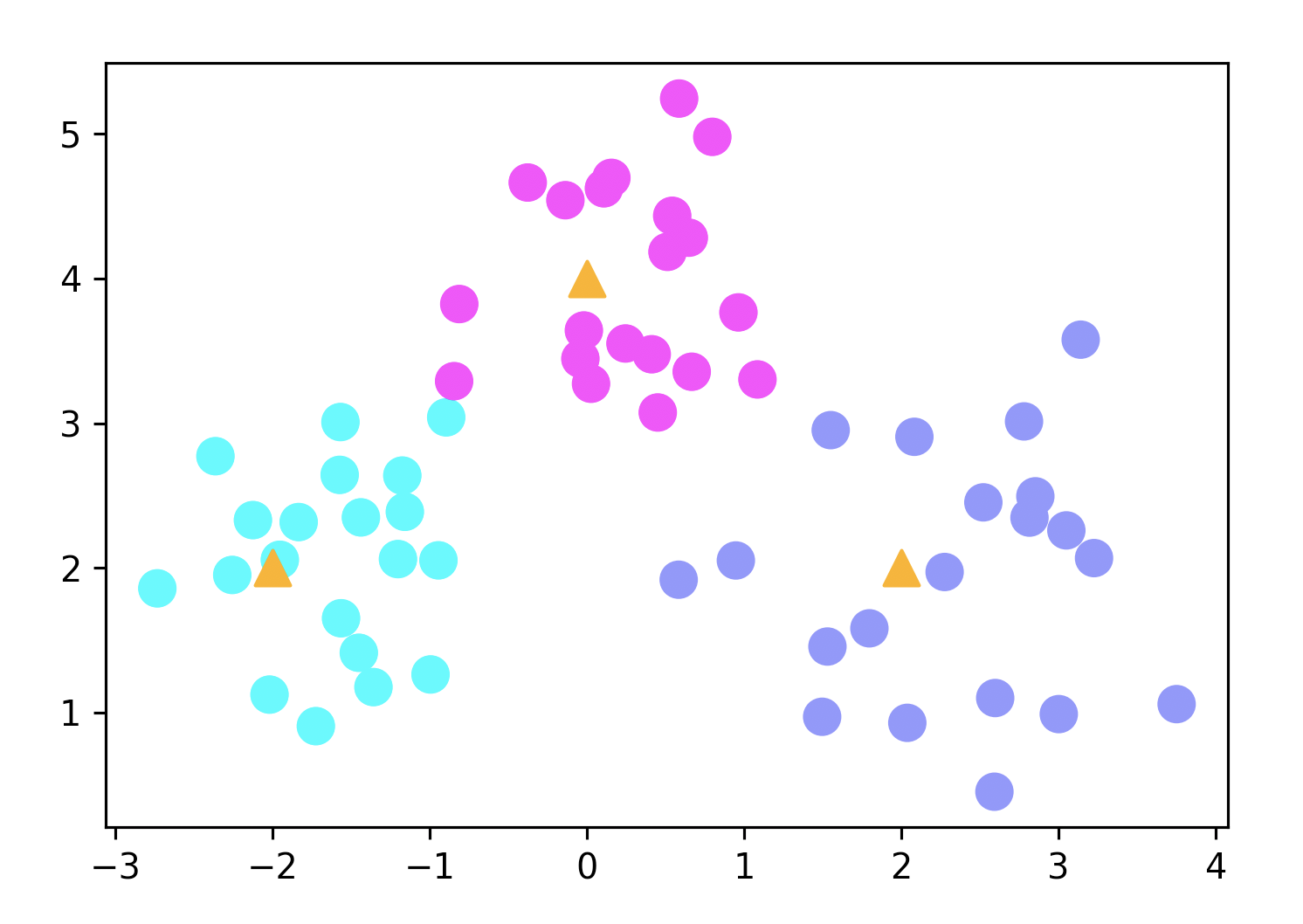
图形中显示的三个三角形的点就是中心点,围绕在它们周围的圆点就是我们随机生成的数据的点。
3 KNN算法对数据的训练
# 从sklearn库中导入K邻居分类器:KNeighbosrClassifier
from sklearn.neighbors import KNeighborsClassifier
# 设定K值
k = 5
# 声明k临近分类器对象
clf = KNeighborsClassifier(n_neighbors=k)
# 训练模型
clf.fit(x, y)
4 预测样本数据
# 定义样本数据
x_sample = [[0, 2]]
# 使用模型进预测
neighbors = clf.kneighbors(x_sample, return_distance=False)
print(neighbors)
# 输出值:[[23 39 21 47 29]]
x_sample变量是我们要进行预测的样本,然后使用clf.kneighbors方法就可以对这个样本进行预测了。关于clf.kneighbors的参数return_distance,它决定了是否返回计算后的距离,默认是True,这里我把它修改成了False,你如果想要看一下值为True是什么样子,可以自己手动修改为True。到这里你可以有一点懵,这怎么就预测完成了呢?输出值表示的是什么意思呢?
输出值表示的是5个经过计算之后的位于x训练集中的索引值,它们并不是直接的位置。
5 画出预测的结果
为了能够使预测的结果更加直观,我们还需要用代码把他们画出来。
# 把带预测的样本以及和其最近的5个点标记出来
plt.figure(figsize=(8, 5), dpi=144) # dpi是像素值
plt.scatter(x[:, 0], x[:, 1], c=y, s=100, cmap='cool') # 样本数据
plt.scatter(c[:, 0], c[:, 1], s=100, marker='^', c='k') # 中心点
# 带预测的点
plt.scatter(x_sample[0][0], x_sample[0][1], marker='x', s=100, cmap='cool')
# 把预测点与距离最近的5个样本连成线
for i in neighbors[0]:
plt.plot([x[i][0], x_sample[0][0]], [x[i][1], x_sample[0][1]], 'k--', linewidth=0.6)
plt.show()
显示结果如下图所示:
三 花卉识别项目练习
1 先认识三朵花
在这一小节我们将通过一个花卉识别项目的练习来巩固我们所讲的KNN算法,训练数据集是非常著名的鸢尾花数据集,涉及到的花的种类一共分为三种:
第一种花是山鸢尾,长下面这个样子
第二种花是锦葵,也叫虹膜锦葵
第三种花是变色鸢尾
2 导入数据集
我们可以通过sklearn库的自带数据集直接引入鸢尾花的数据集,在这个数据集中,我们可以通过花萼长度,花萼宽度,花瓣长度和花瓣宽度四个属性来预测未标记的鸢尾花属于哪个类别。
# 1 导入鸢尾花数据集
from sklearn.datasets import load_iris
# 2 声明一个鸢尾花的类对象
iris = load_iris()
# 3 获取鸢尾花的数据
iris_data = iris.data
# 4 获取数据对应的种类
iris_target = iris.target
print(iris_data)
print(iris_target)
查看数据后你会看到iris_data变量里每一个元素一共有4个值,这四个值就是分别对应花萼长度、花萼宽度、花瓣长度、花瓣宽度4个属性,iris_target变量对应的就是每一个花所属的类别。一共对应的是3个类别,0的意思是山鸢尾,1是虹膜锦葵,2是变色鸢尾。
3 训练模型
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split # 分割训练集和测试集
from sklearn.neighbors import KNeighborsClassifier
iris = load_iris()
iris_data = iris.data
iris_target = iris.target
# 把数据分为训练集和测试集,x表示特征值,y表示目标值,test_size=0.25表示将25%的数据用作测试集
x_train, x_test, y_train, y_test = train_test_split(iris_data, iris_target, test_size=0.25)
# 创建KNN算法实例,n_neighbors参数默认为5,后续可以通过网格搜索获取最优参数
knn = KNeighborsClassifier(n_neighbors=5)
# 训练测试集数据
knn.fit(x_train, y_train)
# 获取预测结果
y_predict = knn.predict(x_test)
# 展示预测结果
labels = ['山鸢尾', '虹膜锦葵', '变色鸢尾']
for i in range(len(y_predict)):
print('第%d次测试:预测值:%s 真实值:%s' %((i + 1), labels[y_predict[i]], labels[y_test[i]]))
print('准确率:', knn.score(x_test, y_test))
4 获取k值最优参数
k值选取的思路是我们先来选择一个k值的范围,把这个范围中所有的误差值都获取到,然后我们再来选择误差最小的值作为k值。
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
# 中文显示
plt.rcParams["font.family"] = 'Arial Unicode MS'
# 导入数据集
iris = load_iris()
x = iris.data
y = iris.target
# 限制k的取值范围
k_range = range(1, 31)
# 记录每当k值变换一次,它的错误值是多少
k_error = []
for k in k_range:
knn = KNeighborsClassifier(n_neighbors=k)
# cv参数决定数据集划分比例,这里按照5:1划分训练集和测试集
scores = cross_val_score(knn, x, y, cv=6)
print(scores)
k_error.append(1 / scores.mean())
# 把结果画成图,直观看出k取什么值误差最小,x轴为k值,y轴为误差值
plt.plot(k_range, k_error)
plt.xlabel('k值')
plt.ylabel('误差值')
plt.show()
图形显示结果如下图所示: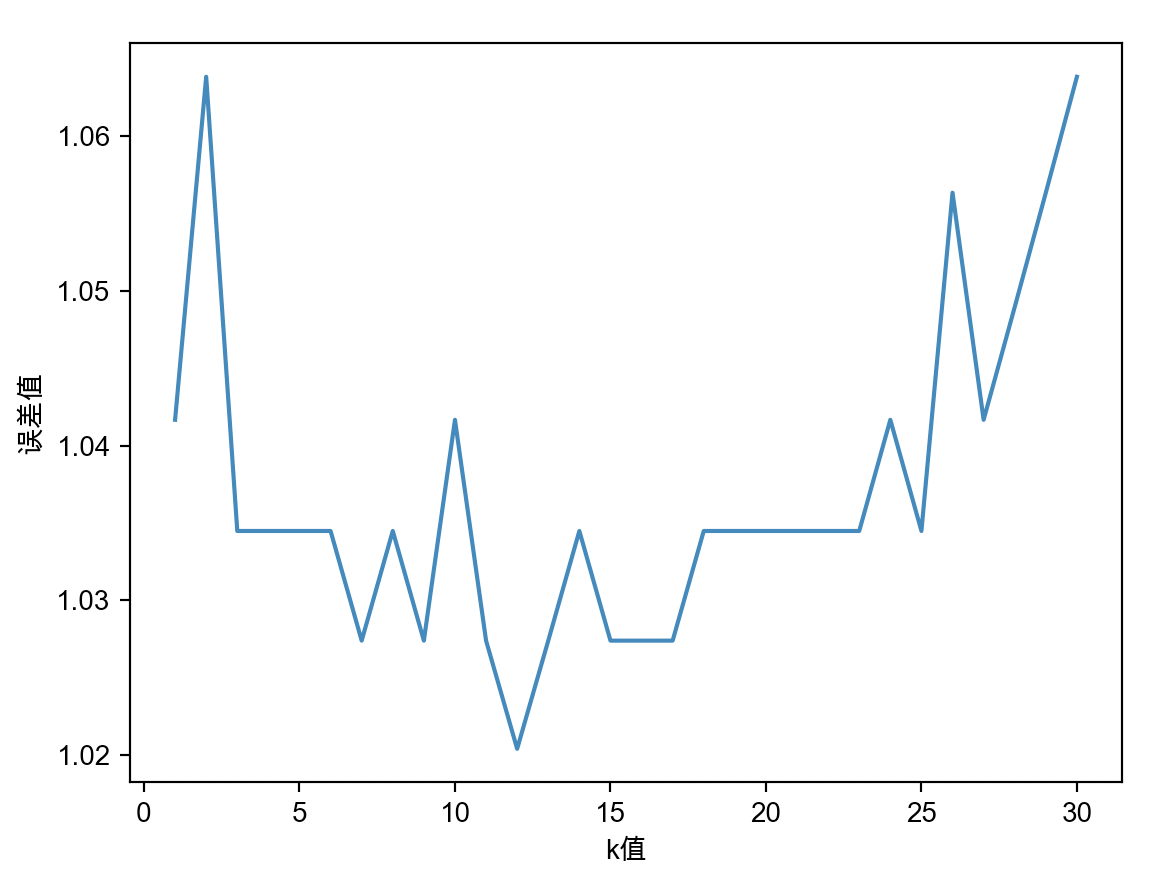
根据这个图形我们就可以看得出来,k值大概是在12这个位置时,误差是最小的。这时当我们把12重新放入到之前的代码中,可能你会发现他的准确率并没有提升甚至还有可能下降了,其实是因为数据量比较小的缘故,并不影响我们解决问题的方式。
四 KNeighborsClassifier参数详解
通过前面的练习,相信你已经基本掌握了KNeighborsClassifier的使用方法了,最后,在这里我们会对这个方法的参数进行更细致的说明和讲解。
# 查看KNeighborsClassifier源代码
NeighborsClassifier(
n_neighbors=5,
weights="uniform”,
algorithm=”auto“,
leaf_size=30,
p=2,
metric="minkowski",
metric_params=None,
n_jobs=None,
**kwargs,
)
- weights用于指定临近样本的投票权重,默认是uniform,表示所有邻近样本投票权重都是一样的。如果我们把weights的值设置成distance,表示投票权重与距离成反比,也就是说邻近样本与未知类别样本距离越远,则其权重越小,反之,权重越大。
- algorithm用于指定邻近样本的搜寻方法,如果值为ball_tree,表示用球树搜寻法寻找近邻样本,kd_tree就是KD树搜寻法,brute是使用暴力搜寻法。algorithm默认参数是auto,表示KNN算法会根据数据特征自动选择最佳搜寻方法。关于这些搜寻法的细节,我会在未来发布的机器学习的文章中做详细的说明,现在只需要知道我们当前用的是默认的自动帮我们选择的搜寻方法。
- leaf_size用于指定球树或者KD树叶子节点所包含的最小样本量,它用于控制树的生长条件,会影响查询速度,默认值是30,目前我们先不关注这个点。
- metric参数是用来指定距离的度量指标,默认为闵可夫斯基距离。
- p参数是依赖metric参数生效的,当metric为minkowski距离时,p=1表示计算点之间的曼哈顿距离,p=2表示计算点之间的欧式距离,默认值为2,计算欧式距离。
- metric_params是一个字典,默认值为空,它为metric参数所对应的距离指标添加关键字参数。
- n_jobs设置KNN算法并行计算时所需的CPU数量,默认值为1,表示仅使用一个CPU运行算法,也就是不开启并行运算。
同样的,最后我们会有一个小的练习,请点击下方链接下载:
chapter9-1.zip