本文将介绍字符串的查找算法:R-way tries和ternary search tries(TST)。
1. 前文回顾
在字符串算法—字符串排序(上篇)和字符串算法—字符串排序(下篇)中,我们介绍了字符串的排序方法。
但如果我们只想进行字符串的查找工作而不想排序呢?
提到查找,我们自然而然地就想起了高效的两种查找算法:搜索算法—红黑树和搜索算法—哈希表。
它们的效率如下图:

注释:图中N为元素的总个数。
先看红黑树,我们可以把每个字符串当成一个节点,然后进行搜索。但是,搜索过程中需要进行数次比较(log2N),每次比较都需两个字符串将所有字符逐一对比,这里相对来说,比较慢。
在看哈希表,因为只需进行很少次数的比较,所以红黑树的比较问题在哈希表中并不严重。但是,想用哈希表算法,我们是需要计算哈希值的,并且消耗一定量的空间。
有没有比红黑树和哈希表更快、更省空间的算法呢?
有!请看下文介绍。
2. R-way tries
这个算法名字在网络上并没找到正统的翻译,我就不翻译过来了。
先从例子中直观地感受一下这棵树:

这里有一堆字符串,每个字符串对应一个数字,数字大小不必在意,反正不重复就行。接下来,把这堆字符串建成树:

这个是R-way tries。应注意到:
1. 根节点为空;
2. 每个节点只有一个字符;
3. 有些节点会有一些数字,而有一些没有。
为了容易理解,我们先介绍如何查找某个字符串,再介绍如何建这棵树。
寻找字符串“she”
首先,she的第一个字符为s,从根节点出发,去找s:
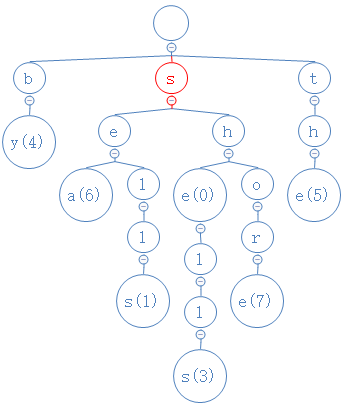
找到s了,然后,she的第二个字符为h,从s出发,去找h:
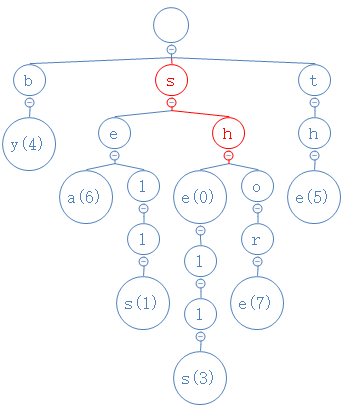
找到h了,然后,she的第三个字符为e,从h出发,去找e:
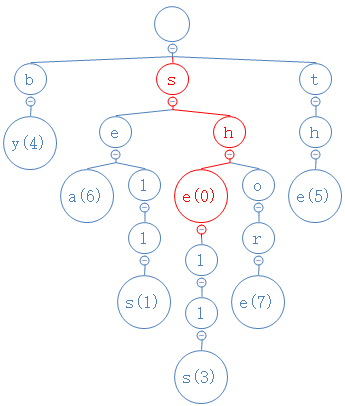
找到e了,然后,she没有第四个字符。看我们找到的e,它有个数字0,因此she在这堆字符串里,且对应的数字为0。
寻找字符串“shell”
首先,shell的第一个字符为s,从根节点出发,去找s:

找到s了,然后,shell的第二个字符为h,从s出发,去找h:

找到h了,然后,shell的第三个字符为e,从h出发,去找e:

找到e了,然后,shell的第四个字符为l,从e出发,去找l:
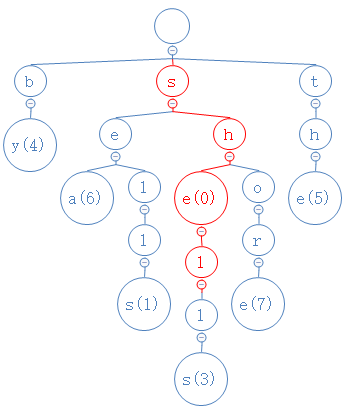
找到l了,然后,shell的第五个字符为l,从l出发,去找l:

找到l了,然后,shell没有第六个字符。看我们找到的l,它没有数字,说明shell不在这堆字符串里。
查找字符串"are"
首先,are的第一个字符为a,从根节点出发,去找a:
找不到!说明are不在这堆字符串里。
通过上述3个字符串的寻找,相信大家已经会看这棵树了,接下来介绍建树的方法:
首先建个空节点作为根,然后逐一输入字符串:(输入顺序随意)
输入字符串“she”,对应数字为0:
首先,she的第一个字符为s,从根节点出发,去找s;
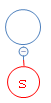
结果s不存在,在根节点下面建一个空节点,并把s放进去:
she的第二个字符为h,从s出发,去找h;
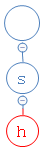
结果h不存在,在s下面建一个空节点,并把h放进去:
she的第三个字符为e,从h出发,去找e;
结果e不存在,在h下面建一个空节点,并把e放进去:

she没第四个字符,把对应的数字填入e里:

输入字符串“shells”,对应数字为3:
首先,shells的第一个字符为s,从根节点出发,去找s;
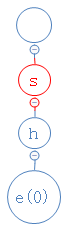
shells的第二个字符为h,从s出发,去找h;
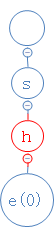
shells的第三个字符为e,从h出发,去找e;

shells的第四个字符为l,从e出发,去找l;
结果l不存在,在e下面建一个空节点,并把l放进去:

shells的第四个字符为l,从e出发,去找l;
结果l不存在,在e下面建一个空节点,并把l放进去:
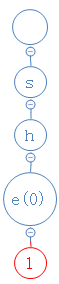
shells的第五个字符为l,从l出发,去找l;
结果l不存在,在l下面建一个空节点,并把l放进去:

shells的第六个字符为s,从l出发,去找s;
结果s不存在,在l下面建一个空节点,并把s放进去:

shells没第七个字符,把对应的数字填入s里:

输入字符串“sea”,对应数字为6:
首先,sea的第一个字符为s,从根节点出发,去找s;

sea的第二个字符为e,从s出发,去找e;
结果e不存在,在s下面建一个空节点,并把e放进去:
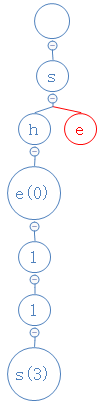
sea的第三个字符为a,从e出发,去找a;
结果a不存在,在e下面建一个空节点,并把a放进去;
并且sea没第四个字符,把对应的数字放进a里:
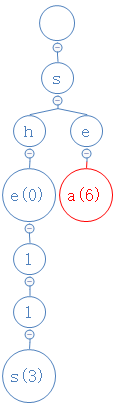
注意,在R-way tries里,新建的节点在已有的节点左边还是右边都无所谓。
如此类推,把所有字符串全部输入进去后,树建成:

到现在为止,我们知道了如何去建树和用树去找字符串,还缺什么操作?删除!
删除也很简单,例如
删除shells:
首先,按照查找方法,从根节点开始,逐个字符地找到shells的最后一个字符:
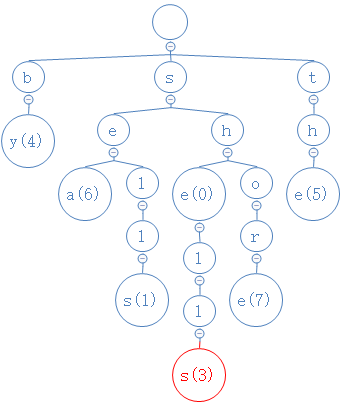
然后把这个s的数字删掉:
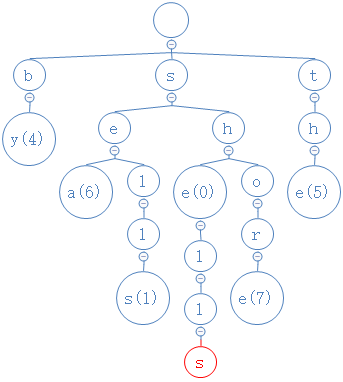
然后检查s是否有非空子节点,结果没有,把s删掉:

然后检查s的上一个节点l是否有非空子节点或者数字,结果都没有,把l删掉:
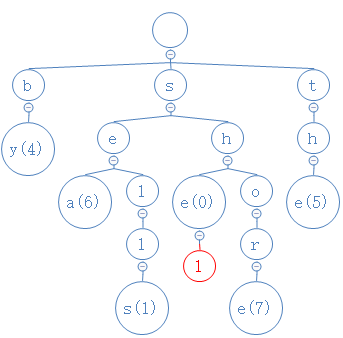
然后检查l的上一个节点l是否有非空子节点或者数字,结果都没有,把l删掉:

然后检查l的上一个节点e是否有非空子节点或者数字,结果有数字,删除操作结束。
原则上,R-way tries里不允许出现即没非空子节点又没数字的节点。
从原理上来看,一切都是多么的美好!但用代码实现时,就会遇到一个严重的问题。
每个节点都有一个节点数组,用来存储此节点的子节点。那么,这个数组建立的时候,应该建多大?
每个节点会有多少个子节点?这要看输入的字符串里的字符总共有多少种字符。
如果我们能保证输入的字符串全都是字母,那么每个节点最多有26个子节点(因为只有26个字母),即每个节点的数组应该能容纳26个元素。

根据具体情况来选择R值吧,每个节点最多有R个子节点,即每个节点的数组应该能容纳R个元素。
此时,再看回我们的这个例子:

假设我们输入的字符串的字符串全都是字母,那么每个节点都有26个子节点,但实际用到的只有几个,其余全都是空节点,这是对内存的极大浪费!
放心,下面会介绍优化方法。
先看回R-way tries的实现代码:

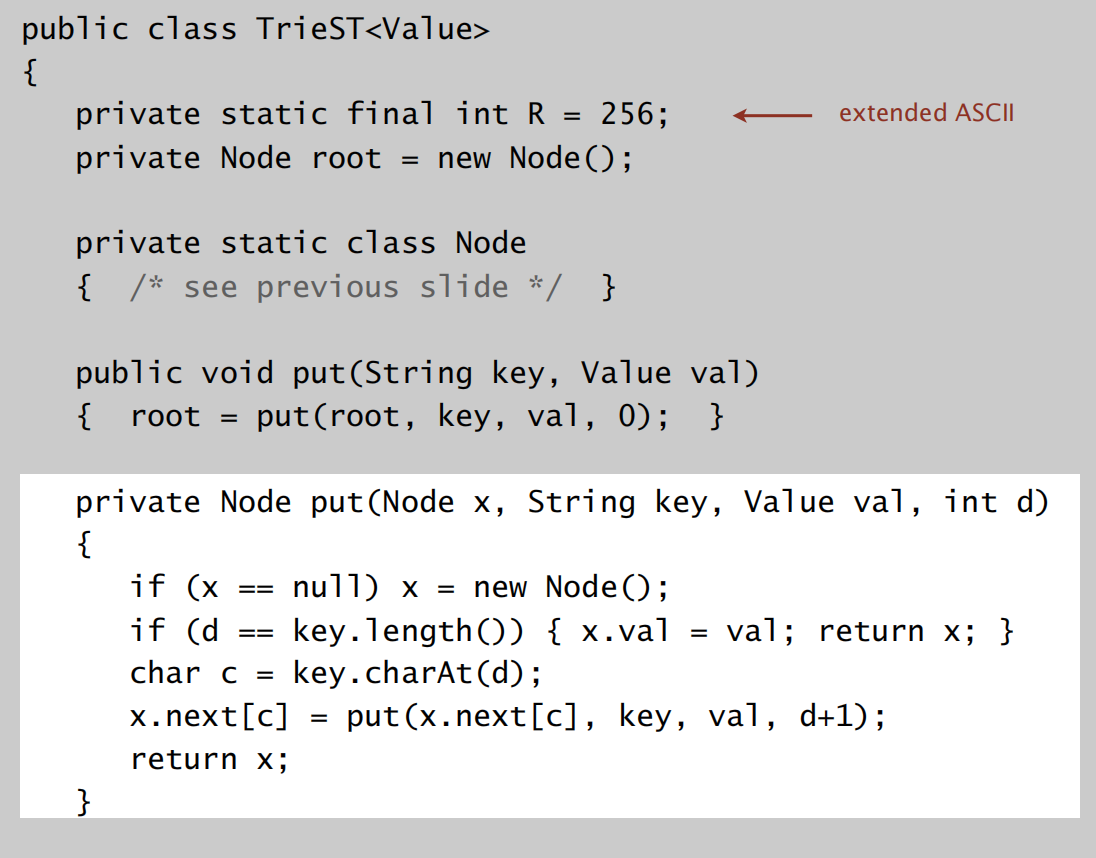

再看R-way tries的效率:
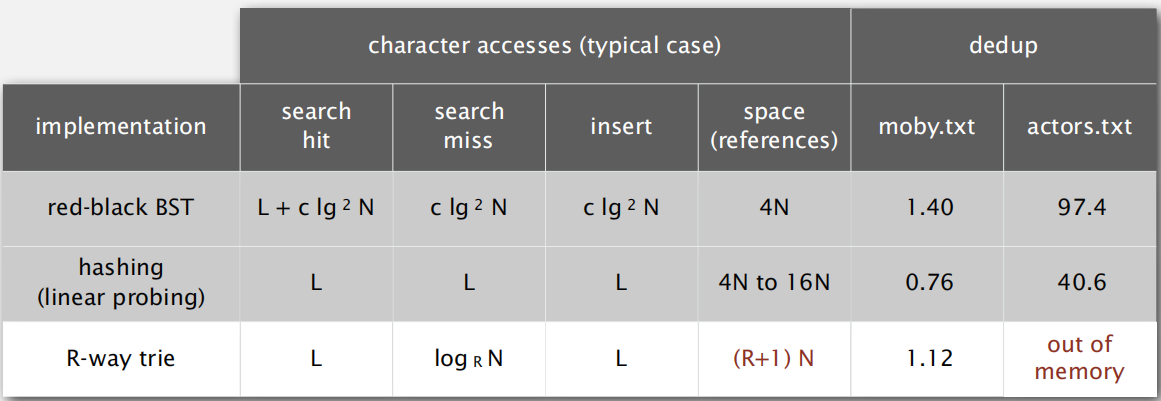
注释:
1. N为所有字符串的总个数。
2. L为字符串的长度
3. R为我们选择的R值(上文提及的R)

4. moby.txt和actors.txt是测试文件。
从图中可看出,R-way tries比红黑树快,比哈希表慢,且如果字符串过多,则内存有可能原地爆炸。
3. ternary search tries
这个名字直译过来就是三叉搜索树,但是网络上没看到正统的翻译,所以这里也保留了英文原名。
ternary search tries简称TST。它是R-way tries的进化版。
每个节点都有三个子节点,左边的子节点比此节点小,中间的子节点等于此节点,右边的子节点比此节点大。
从一个例子直观的感受一下:(有些空节点标出来是为了避免歧义)

与R-way tries有点像,但根节点不再为空,且找字符串的方法要些许不同。TST的节点最多有3个节点。
先来看查找字符串:
寻找字符串“by”
by的第一个字符为b,与根节点对比,b<s,故去s的左节点比较,然后发现s的左节点为b,相等:
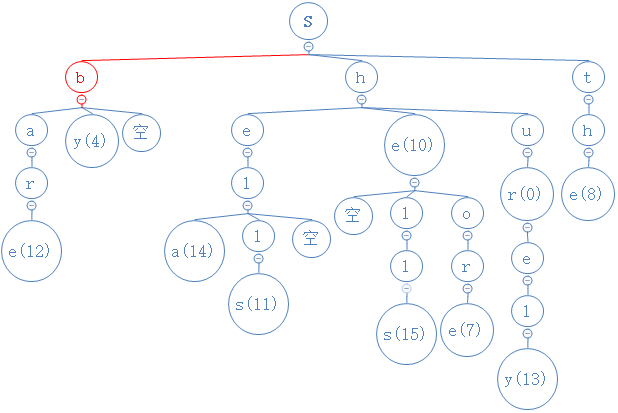
by的第二字符为y,从目前所处的b节点出发,与此节点的中间节点相比较,相等:
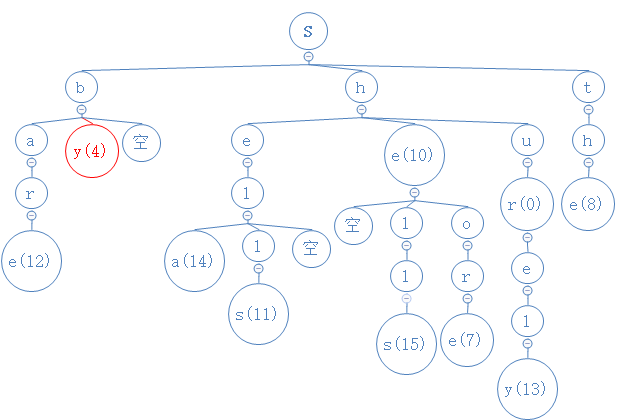
by没第三个字符,我们找到的节点y有数字4,故查找成功,by对应的数字为4。
寻找字符串“shor”
shor的第一个字符为s,与根节点对比,s=s,:

shor的第二个字符为h,从目前所处的s节点出发,与此节点的中间节点相比较,相等:
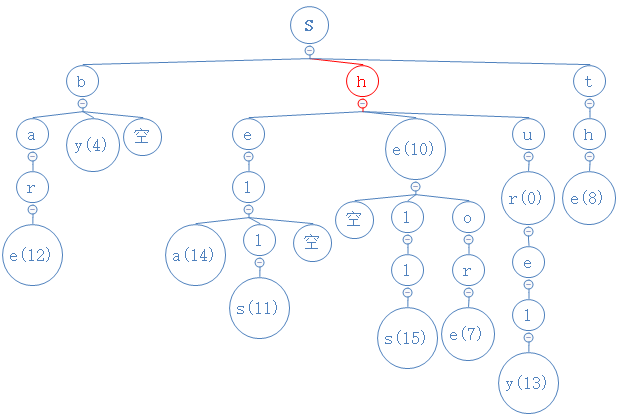
shor的第三个字符为e,从目前所处的h节点出发,与此节点的中间节点相比较,o>e,故去此节点的右节点中进行比较,相等:

shor的第四个字符为r,从目前所处的o节点出发,与此节点的中间节点相比较,相等:
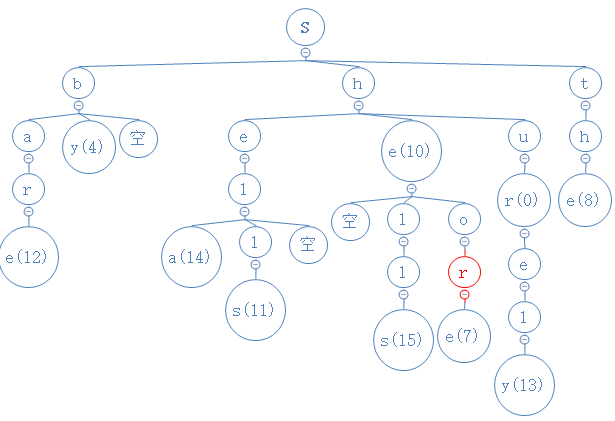
shor没第五个字符,我们找到的节点r没有数字,故查找失败,shor不在这堆字符串里。
总结一下:
1. 假设要查找的字符串为X;整数变量int d=1; 节点Node=根节点;
2. 把X的第d个字符与Node节点进行比较,如果这个字符大,则去根Node的右节点A,且Node=A; 如果这个字符小,则去Node的左节点B,且Node=B;如果相等,去第4步;
3. 重复第2步,直到找到与X的第d个字符相等的节点为止,如果找不到,则说明要查找的字符串X不存在。
4. d+=1; Node=Node的中间节点C;如果C不存在,且d<=X的长度,则说明要查找的字符串X不存在。重复第二步,直到d>X的长度为止,此时,去第5步;
5. 检查X的最后一个字符所在的节点(即现在的Node)是否有数字,如果有,则说明找到这个字符串了;如果没有,则找不到。
看懂了查找字符串,添加字符串也差不多了:
添加字符串“share”,对应数字为16:
share的第一个字符为s,与根节点进行比较,相等:

share的第二个字符为h,与s节点的中间节点进行比较,相等:

share的第三个字符为a,与h节点的中间节点进行比较,a小;
去与h的左节点e进行比较,a小;
e节点左节点为空节点,把a填进去:
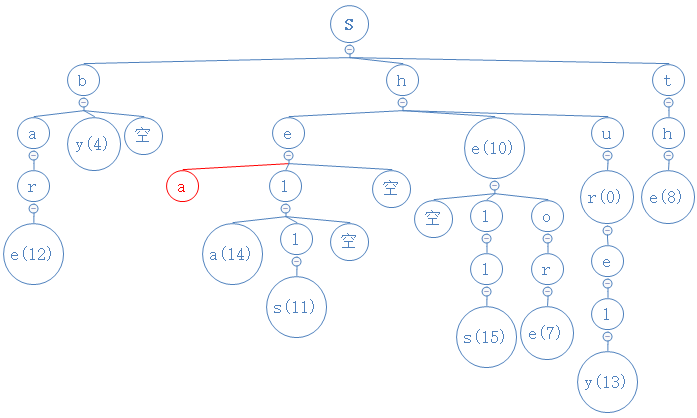
share的第四个字符为r,与a节点的中间节点进行比较,发现中间节点为空节点,把r填进去:

share的第五个字符为e,与r节点的中间节点进行比较,发现中间节点为空节点,把e填进去,且由于share没第六个字符,把数字也进去:
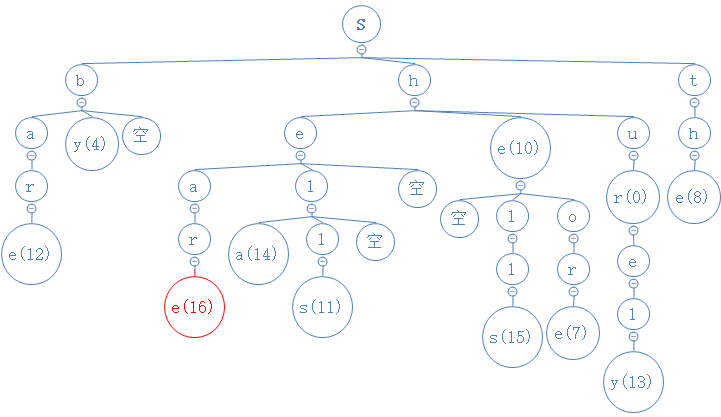
添加完毕。
删除操作与R-way tries的一模一样,这里不做累述。
实现代码:
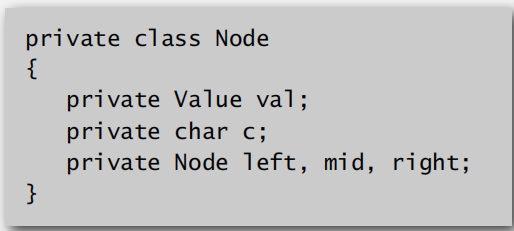
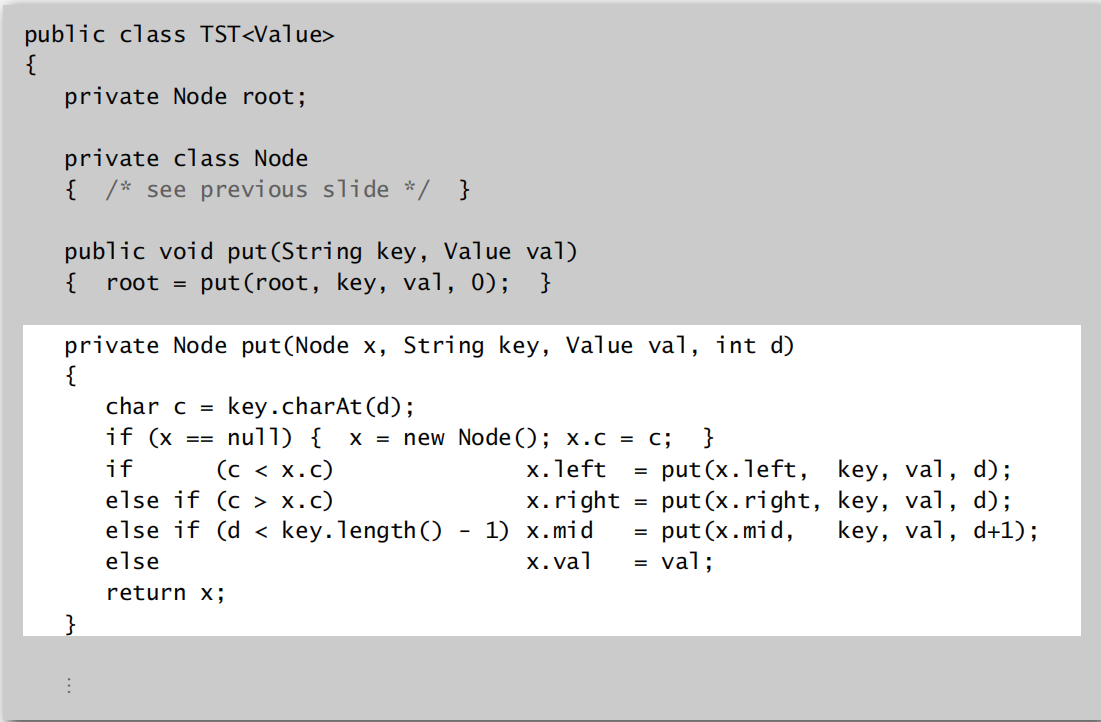

TST的效率:

注释:
1. N为所有字符串的总个数。
2. L为字符串的长度
3. R为我们选择的R值(上文提及的R)

4. moby.txt和actors.txt是测试文件。
TST速度上比哈希表还要快,占用的空间相对来说也不多!
4. 算法应用
字符串排序:
在TST的基础上是可以进行字符串排序的,只需从最左边一直读到最右边即可。
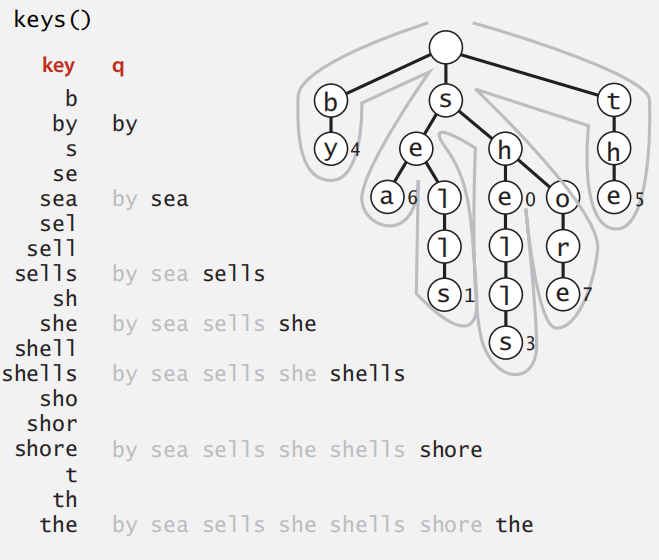
代码实现:

搜索引擎:

像google这类的引擎,我们可以用TST来实现。
例如在我们上述的例子中:

当我们输入了"she",我们先搜索she:
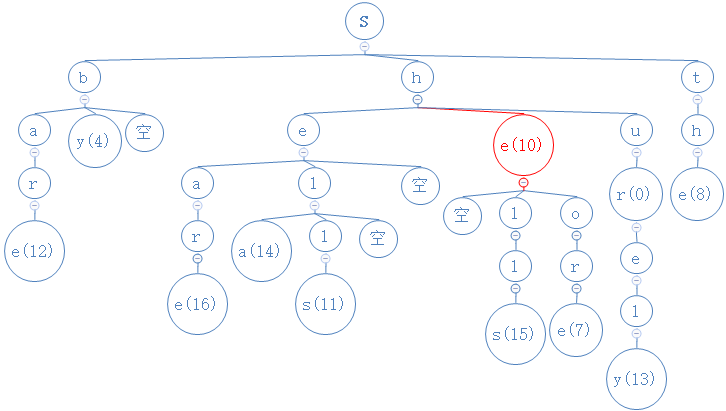
经过3次键索后,找到了she,然后我们发现e下面有非空节点,继续往下走,就可以得到共用“she”的字符串:she,shells,sheore。
实现代码:
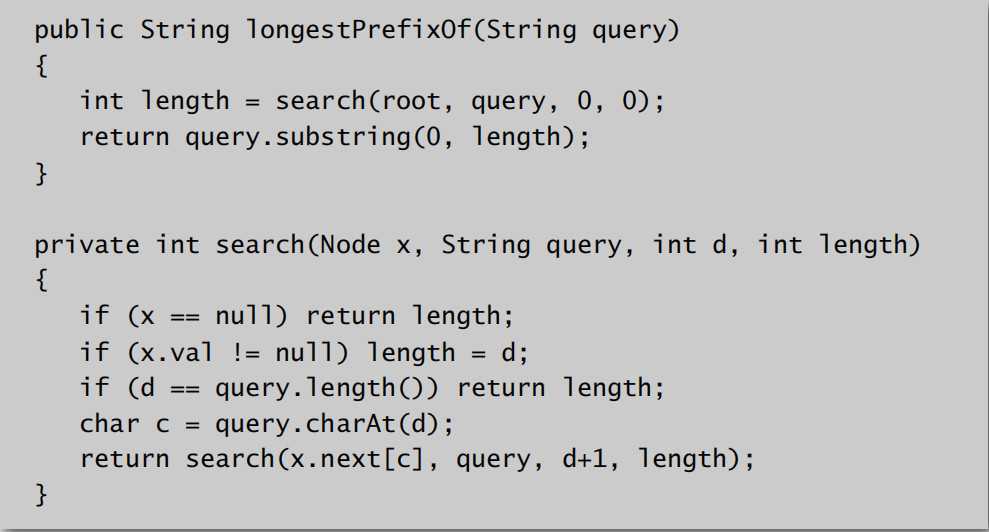
TST的应用还有很多,这里不一一列举。