CodeForces

题意

https://vjudge.net/problem/CodeForces-1230E

给出一棵树, 点上有权值, 对于每个点, 求它和所有后代节点的GCD的和.

思路

对于一个点，他对后代的贡献包含他自己和他的各个父亲对后代的贡献。

比如下面这个栗子：

 

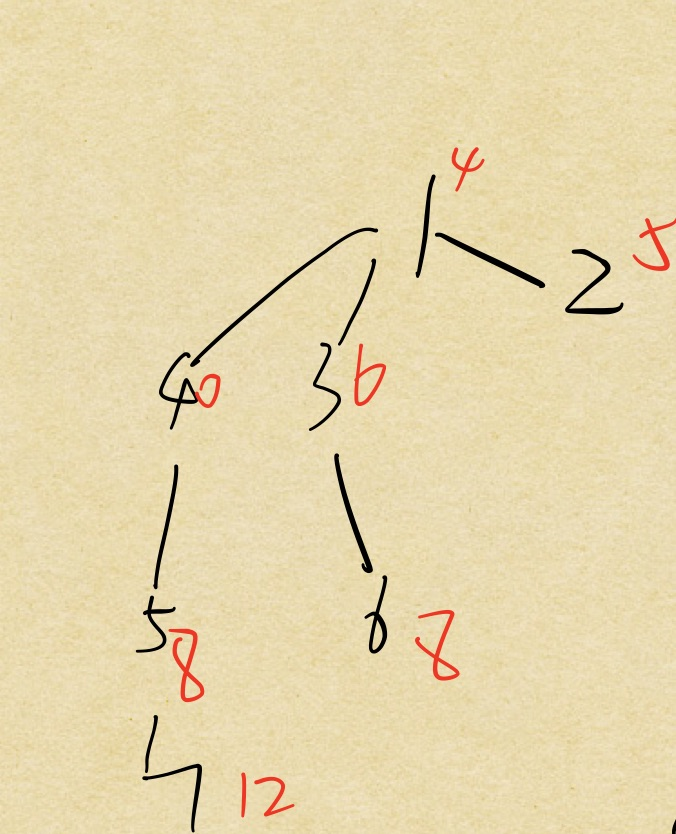
 红色为点权。

那么对于1号点，没有父亲，记录自身的贡献4。对于4号点，父亲是1，用父亲的贡献和4号点的权值取gcd，就是1对4的贡献4，还有自身的贡献0。对于5号点，父亲是4，4对5的贡献包含4到5、1到5的贡献，一样，分别取gcd即为各父亲到5的贡献。

这个过程可以用二维map记录状态，map[u][tmp]表示对于u的各父亲及u的贡献为tmp的个数，map可以在每次dfs往下搜的时候更新。

具体看代码。

代码

#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
#define ll long long
const int N=200005;
const int mod=1e9+7;
const double eps=1e-8;
const double PI = acos(-1.0);
#define lowbit(x) (x&(-x))
ll a[N],ans=0;
map<ll,int> mp[N];
vector<int> g[N];
void dfs(int u,int fa)
{
    for(auto i:mp[fa])
    {
        ll tmp=__gcd(i.first,a[u]);
        mp[u][tmp]+=i.second;
        ans=(ans+i.second*tmp%mod)%mod;
    }
    mp[u][a[u]]++;
    ans=(ans+a[u])%mod;
    for(int v:g[u])
    {
        if(v!=fa)
            dfs(v,u);
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    for(int i=1;i<n;i++)
    {
        int u,v;
        cin>>u>>v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    dfs(1,0);
    cout<<ans<<endl;
    return 0;
}