算法复习_动态规划（矩阵链相乘，最长公共子序列，最长递增子序列）

from http://www.cnblogs.com/huenchao/p/5947403.html

1、矩阵乘法

　

　　

 

 

 

　　

　　从定义可以看出：只有当矩阵A的列数与矩阵B的行数相等时A×B才有意义。一个m×r的矩阵A左乘一个r×n的矩阵B，会得到一个m×n的矩阵C。在计算机中，一个矩阵说穿了就是一个二维数组。一个m行r列的矩阵可以乘以一个r行n列的矩阵，得到的结果是一个m行n列的矩阵，其中的第i行第j列位置上的数等于前一个矩阵第i行上的r个数与后一个矩阵第j列上的r个数对应相乘后所有r个乘积的和。采用C++语言实现完整的两个矩阵乘法，程序如下所示：

 1 #include <iostream>
 2 using namespace std;
 3 #define A_ROWS        3
 4 #define A_COLUMNS     2
 5 #define B_ROWS        2
 6 #define B_COLUMNS     3
 7 void matrix_multiply(int A[A_ROWS][A_COLUMNS],int B[B_ROWS][B_COLUMNS],int C[A_ROWS][B_COLUMNS]);
 8 int main()
 9 {
10     int A[A_ROWS][A_COLUMNS] = {1,0,
11                                 1,2,
12                                 1,1};
13     int B[B_ROWS][B_COLUMNS] = {1,1,2,
14                                 2,1,2};
15     int C[A_ROWS][B_COLUMNS] = {0};
16     matrix_multiply(A,B,C);
17     for(int i=0;i<A_ROWS;i++)
18     {
19         for(int j=0;j<B_COLUMNS;j++)
20             cout<<C[i][j]<<" ";
21         cout<<endl;
22     }
23     return 0;
24 }
25 void matrix_multiply(int A[A_ROWS][A_COLUMNS],int B[B_ROWS][B_COLUMNS],int C[A_ROWS][B_COLUMNS])
26 {
27     if(A_COLUMNS != B_ROWS)
28         cout<<"error: incompatible dimensions."<<endl;
29     else
30     {
31         int i,j,k;
32         for(i=0;i<A_ROWS;i++)
33             for(j=0;j<B_COLUMNS;j++)
34             {
35                 C[i][j] = 0;
36                 for(k=0;k<A_COLUMNS;k++)
37                     C[i][j] += A[i][k] * B[k][j]; //将A的每一行的每一列与B的每一列的每一行的乘积求和
38             }
39     }
40 }

程序测试结果如下所示：

2、矩阵链乘问题描述

　　给定n个矩阵构成的一个链<A₁,A₂,A₃,.......A_n>，其中i=1,2,...n，矩阵A的维数为p_i-1p_i，对乘积 A₁A₂...A_n 以一种最小化标量乘法次数的方式进行加全部括号。

　　注意：在矩阵链乘问题中，实际上并没有把矩阵相乘，目的是确定一个具有最小代价的矩阵相乘顺序。找出这样一个结合顺序使得相乘的代价最低。

3、动态规划分析过程

1）最优加全部括号的结构

　　动态规划第一步是寻找一个最优的子结构。假设现在要计算A_iA_i+1....A_j的值，计算A_i...j过程当中肯定会存在某个k值（i<=k<j）将A_i...j分成两部分，使得A_i...j的计算量最小。分成两个子问题A_i...k和A_k+1...j，需要继续递归寻找这两个子问题的最优解。

　　有分析可以到最优子结构为：假设A_iA_i+1....A_j的一个最优加全括号把乘积在A_k和A_k+1之间分开，则A_i..k和A_k+1..j也都是最优加全括号的。

2）一个递归解

　　设m[i,j]为计算机矩阵A_i...j所需的标量乘法运算次数的最小值，对此计算A_1..n的最小代价就是m[1,n]。现在需要来递归定义m[i,j]，分两种情况进行讨论如下：

当i==j时：m[i,j] = 0，（此时只包含一个矩阵）

当i<j 时：从步骤1中需要寻找一个k（i≤k＜j）值，使得m[i,j] ＝min{m[i,k]+m[k+1,j]+p_i-1p_kp_j} （i≤k＜j）。

3）计算最优代价

　　虽然给出了递归解的过程，但是在实现的时候不采用递归实现，而是借助辅助空间，使用自底向上的表格进行实现。设矩阵Ai的维数为pi-1pi，i=1,2.....n。输入序列为：p=<p0，p1,...pn>，length[p] = n+1。使用m[n][n]保存m[i,j]的代价，s[n][n]保存计算m[i,j]时取得最优代价处k的值，最后可以用s中的记录构造一个最优解。书中给出了计算过程的伪代码，摘录如下：

 1 // p是数组，表示维度
 2 Matrix_Chain_Order = function (p) {
 3 
 4     var n = p.length - 1; //表示几个矩阵
 5     var m = []; //存最大值
 6     var s = []; //存路径
 7 
 8 
 9     //m[0][1] 表示一个矩阵
10     for (var i = 0; i <= n; i++) {
11         m[i] = [];
12         s[i] = [];
13         for (var j = 0; j <= n; j++) {
14 
15             m[i][j] = 0;
16             s[i][j] = 0;
17         }
18 
19     }
20 
21 
22     //表示几个矩阵相乘
23     for (var l = 2; l <= n; l++) {
24 
25         for (var i = 1; i + l - 1 <= n; i++) {
26 
27             var j = i + l - 1;
28 
29             m[i][j] = Number.MAX_VALUE;
30 
31             for (var k = i; k < j; k++) {
32 
33                 var temp = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
34 
35                 if (m[i][j] > temp) {
36 
37                     m[i][j] = temp;
38                     s[i][j] = k;
39                 }
40 
41             }
42         }
43     }
44 
45     return {
46         m: m,
47         s: s
48     };
49 };
50 
51 
52 var p = [30, 35, 15, 5, 10, 20, 25];
53 
54 var str = "";
55 
56 //构造最优势解
57 function Print_Optimal_Parens(s, i, j) {
58 
59     if (i === j) {
60 
61         str += "A" + i;
62 
63     } else {
64         str += "(";
65         Print_Optimal_Parens(s, i, s[i][j]);
66         Print_Optimal_Parens(s, s[i][j] + 1, j);
67 
68         str += ")";
69 
70 
71     }
72 
73 
74 }
75 
76 
77  var obj = Matrix_Chain_Order(p);
78  var s = obj.s;
79  console.log(obj.m)
80  console.log(obj.s)
81  Print_Optimal_Parens(s, 1, s.length - 1);
82  console.log(str)

一、动态规划算法

 

   事实上，最长公共子序列问题也有最优子结构性质。

   记：

   Xi = <x1,x2,x3,....xi>即X序列的前i个字符（1<= i <= m）(前缀)

   Yj = <y1,y2,y3,....yi>即Y序列的前j个字符（1<= j <= m）(前缀)

   

   假定Z = <z1,z2,z3,...zk>是LCS（X,Y)中的一个。

   ·若xm = yn（最后一个字符相同），则不难用反正法证明：该字符必是X与Y的任一最长公共子序列Z（设长度为k）的最后一个字符，即有zk = xm = yn，且显然有Zk-1∈LCS(Xm-1,Yn-1)，即Z的前缀Zk-1是Xm-1与Yn-1的最长公共子序列。此时，问题化归成求Xm-1与Yn-1的LCS（LCS(X,Y)）的长度等于LCS(Xm-1,Yn-1)的长度加1）。

   ·若xm≠yn，则亦不难用反证法证明：要么Z∈LCS(Xm-1, Y)，要么Z∈LCS(X , Yn-1)。由于zk≠xm与zk≠yn其中至少有一个必成立，若zk≠xm则有Z∈LCS(Xm-1 , Y)；类似的，若zk≠yn 则有Z∈LCS(X , Yn-1)。此时，问题化归成求Xm-1与Y的LCS及X与Yn-1的LCS。LCS(X , Y)的长度为：max{LCS(Xm-1 , Y)的长度, LCS(X , Yn-1)的长度}。

 

   由于上述当xm≠yn的情况中，求LCS(Xm-1 , Y)的长度与LCS(X , Yn-1)的长度，这两个问题不是相互独立的：两者都需要求LCS(Xm-1，Yn-1)的长度。另外两个序列的LCS中包含了两个序列的前缀的LCS，故问题具有最优子结构性质考虑用动态规划法。

 

   也就是说，解决这个LCS问题，你要求三个方面的东西：

   1> LCS（Xm-1，Yn-1）+1；

   2> LCS（Xm-1，Y），LCS（X，Yn-1）；

   3> max{LCS（Xm-1，Y），LCS（X，Yn-1）}；

 

二、动态规划算法解LCS问题

 

2.1 最长公共子序列的结构

 

   最长公共子序列的结构有如下表示：

   

   设序列X=<x1, x2,="" …,="" xm="">和Y=<y1, y2,="" …,="" yn="">的一个最长公共子序列Z=<z1, z2,="" …,="" zk="">，则：

   1> 若 xm=yn，则 zk=xm=yn，且Zk-1是Xm-1和Yn-1的最长公共子序列； 

   2> 若 xm≠yn且 zk≠xm ，则 Z是 Xm-1和 Y的最长公共子序列；

   3> 若 xm≠yn且 zk≠yn ，则 Z是 X和 Yn-1的最长公共子序列；

   其中Xm-1=<x1, x2,="" …,="" xm-1="">，Yn-1=<y1, y2,="" …,="" yn-1="">，Zk-1=<z1, z2,="" …,="" zk-1="">。

 

2.2 子问题的递归结构

 

   由最长公共子序列问题的最优子结构性质可知，要找出Xm=<x1, x2,="" …,="" xm="">和Yn=<y1, y2,="" …,="" yn="">的最长公共子序列，可按如下方式递归的进行：

   ·当xm = yn时，找出Xm-1和Yn-1的最长公共子序列，然后在其尾部加上xm或yn，即可得到X和Y的一个最长公共子序列；

   ·当xm≠yn时，必须解两个子问题，即找出Xm-1和Y的一个最长公共子序列及X和Yn-1的一个最长公共子序列。这两个公共子序列中较长者即为X和Y的一个最长公共子序列。

 

   由此递归结构容易看到最长公共子序列问题具有子问题重叠性质。例如，在计算X和Y的最长公共子序列时，可能要计算出X和Yn-1以及Xm-1和Y的最长公共子序列。而这两个子问题都包含一个公共子问题，即计算Xm-1和Yn-1的最长公共子序列。

 

   与矩阵乘积最优计算次序问题类似，我们来建立子问题的最优值的递归关系。用c[i,j]记录序列Xi和Yj的最长公共子序列的长度，其中Xi=<x1, x2,="" …,="" xi="">，Yj=<y1, y2,="" …,="" yj="">。当i = 0或j = 0时，空序列是Xi和Yj的最长公共子序列，故c[i,j] = 0。其他情况下，可得递归关系如下所示：

 

   

2.3 计算最优值

 

   直接利用上节节末的递归式，我们将很容易就能写出一个计算c[i,j]的递归算法，但其计算时间是随输入长度指数增长的。由于在所考虑的子问题空间中，总共只有O(m*n)个不同的子问题，因此，用动态规划算法自底向上地计算最优值能提高算法的效率。

 

   计算最长公共子序列长度的动态规划算法LCS_Length(X,Y)，以序列X=<x1, x2,="" …,="" xm="">和Y=<y1, y2,="" …,="" yn="">作为输入。输出两个数组c[0..m ,0..n]和b[1..m ,1..n]。其中c[i,j]存储Xi与Yj的最长公共子序列的长度，b[i,j]记录指示c[i,j]的值是由哪一个子问题的解达到的，这在构造最长公共子序列时要用到。最后，X和Y的最长公共子序列的长度记录于c[m,n]中。

 

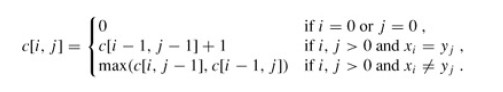
 1 function LCS(A, B) {
 2 
 3     var m = A.length;
 4     var n = B.length;
 5     var C = [];
 6     var b = [];
 7 
 8     for (var i = 0; i <= m; i++) {
 9         C[i] = [];
10         b[i] = [];
11         for (var j = 0; j <= n; j++) {
12 
13             C[i][j] = 0;
14             b[i][j] = 0;
15         }
16     }
17 
18 
19     for (var i = 1; i <= m; i++) {
20         for (var j = 1; j <= n; j++) {
21             if (A[i - 1] == B[j - 1]) {
22                 C[i][j] = C[i - 1][j - 1] + 1;
23                 b[i][j] = 'left_up';
24             } else {
25                 if (C[i - 1][j] >= C[i][j - 1]) {
26                     C[i][j] = C[i - 1][j];
27                     b[i][j] = 'left';
28                 } else {
29                     C[i][j] = C[i][j - 1];
30                     b[i][j] = 'up';
31                 }
32             }
33         }
34     }
35     return {
36         C: C,
37         b: b
38     };
39 }
40 
41 function zuiyou(A, b, i, j) {
42     if (i === 0 || j === 0) {
43         return;
44     }
45     if (b[i][j] == 'left_up') {
46         zuiyou(A, b, i - 1, j - 1);
47         console.log(A[i-1]);
48     } else if (b[i][j] == 'left') {
49         zuiyou(A, b, i - 1, j);
50 
51     } else {
52         zuiyou(A, b, i, j - 1);
53     }
54 }
55 var A = ['A', 'B', 'C', 'B', 'D', 'A', 'B'];
56 var B = ['B', 'D', 'C', 'A', 'B', 'A'];
57 var len_a = A.length;
58 var len_b = B.length;
59 
60 
61 var obj = LCS(A, B);
62 console.log(obj.C);
63 console.log(obj.b);
64 
65 
66 zuiyou(A, obj.b, len_a, len_b);

 最长递增子序列：

一，    最长递增子序列问题的描述

设L=<a₁,a₂,…,a_n>是n个不同的实数的序列，L的递增子序列是这样一个子序列Lin=<a_K1,a_k2,…,a_km>，其中k₁<k₂<…<k_m且a_K1<a_k2<…<a_km。求最大的m值。

二，    第一种算法：转化为LCS问题求解

设序列X=<b₁,b₂,…,b_n>是对序列L=<a₁,a₂,…,a_n>按递增排好序的序列。那么显然X与L的最长公共子序列即为L的最长递增子序列。这样就把求最长递增子序列的问题转化为求最长公共子序列问题LCS了。

最长公共子序列问题用动态规划的算法可解。设Li=< a₁,a₂,…,a_i>,Xj=< b₁,b₂,…,b_j>，它们分别为L和X的子序列。令C[i,j]为Li与Xj的最长公共子序列的长度。则有递推方程看上面。

这可以用时间复杂度为O(n²)的算法求解，由于这个算法上课时讲过，所以具体代码在此略去。求最长递增子序列的算法时间复杂度由排序所用的O(nlogn)的时间加上求LCS的O(n²)的时间，算法的最坏时间复杂度为O(nlogn)＋O(n²)＝O(n²)。

三，    第二种算法：动态规划法

设f(i)表示L中以a_i为末元素的最长递增子序列的长度。则有如下的递推方程：

f[i] = max(f[j]) + 1

这个递推方程的意思是，在求以a_i为末元素的最长递增子序列时，找到所有序号在L前面且小于a_i的元素a_j，即j<i且a_j<a_i。如果这样的元素存在，那么对所有a_j,都有一个以a_j为末元素的最长递增子序列的长度f(j)，把其中最大的f(j)选出来，那么f(i)就等于最大的f(j)加上1，即以a_i为末元素的最长递增子序列，等于以使f(j)最大的那个a_j为末元素的递增子序列最末再加上a_i；如果这样的元素不存在，那么a_i自身构成一个长度为1的以a_i为末元素的递增子序列。

 

 1 var arr = [1, 5, 8, 2, 3, 4];
 2 
 3 function  lis(arr) {
 4 
 5     var n = arr.length;
 6     var c = [];
 7 
 8     for (var i = 0; i <= n; i++) {
 9 
10         c[i] = 0;
11 
12     }
13 
14 
15     for (var j = 1; j <= n; j++) {
16 
17         c[j] = 1;
18 
19         for (var k = 1; k < j; k++) {
20             if (arr[j-1] > arr[k-1] && c[k] >= c[j] - 1) {
21 
22                 c[j] = c[k] + 1;
23 
24             }
25 
26         }
27 
28     }
29 
30     return c;
31 }
32 
33 var c =lis(arr);
34 console.log(c);